9.1 Una estrategia general para modelar funciones de regresión no lineal
Es momento de hechar un vistazo a un ejemplo en que el uso de una función de regresión no lineal es más adecuado para estimar la relación de la población entre el regresor, \(X\), y el regresante, \(Y\): La relación entre los ingresos de los distritos escolares y sus puntajes de prueba.
# preparar los datos
library(AER)
data(CASchools)
CASchools$size <- CASchools$students/CASchools$teachers
CASchools$score <- (CASchools$read + CASchools$math) / 2 Se comienza el análisis calculando la correlación entre ambas variables.
cor(CASchools$income, CASchools$score)
#> [1] 0.7124308Aquí, los ingresos y los puntajes de las pruebas están relacionados positivamente: Los distritos escolares con ingresos por encima del promedio tienden a obtener puntajes por encima del promedio. ¿Una función de regresión lineal modela los datos de manera adecuada? Por tanto, se deben graficar los datos y agregar una línea de regresión lineal.
# ajustar un modelo lineal simple
linear_model<- lm(score ~ income, data = CASchools)
# trazar las observaciones
plot(CASchools$income, CASchools$score,
col = "steelblue",
pch = 20,
xlab = "Ingresos del distrito (miles de dólares)",
ylab = "Resultado de la prueba",
cex.main = 0.9,
main = "Puntuación de la prueba frente a los ingresos del distrito y una función de regresión lineal MCO")
# agregar la línea de regresión al gráfico
abline(linear_model,
col = "red",
lwd = 2)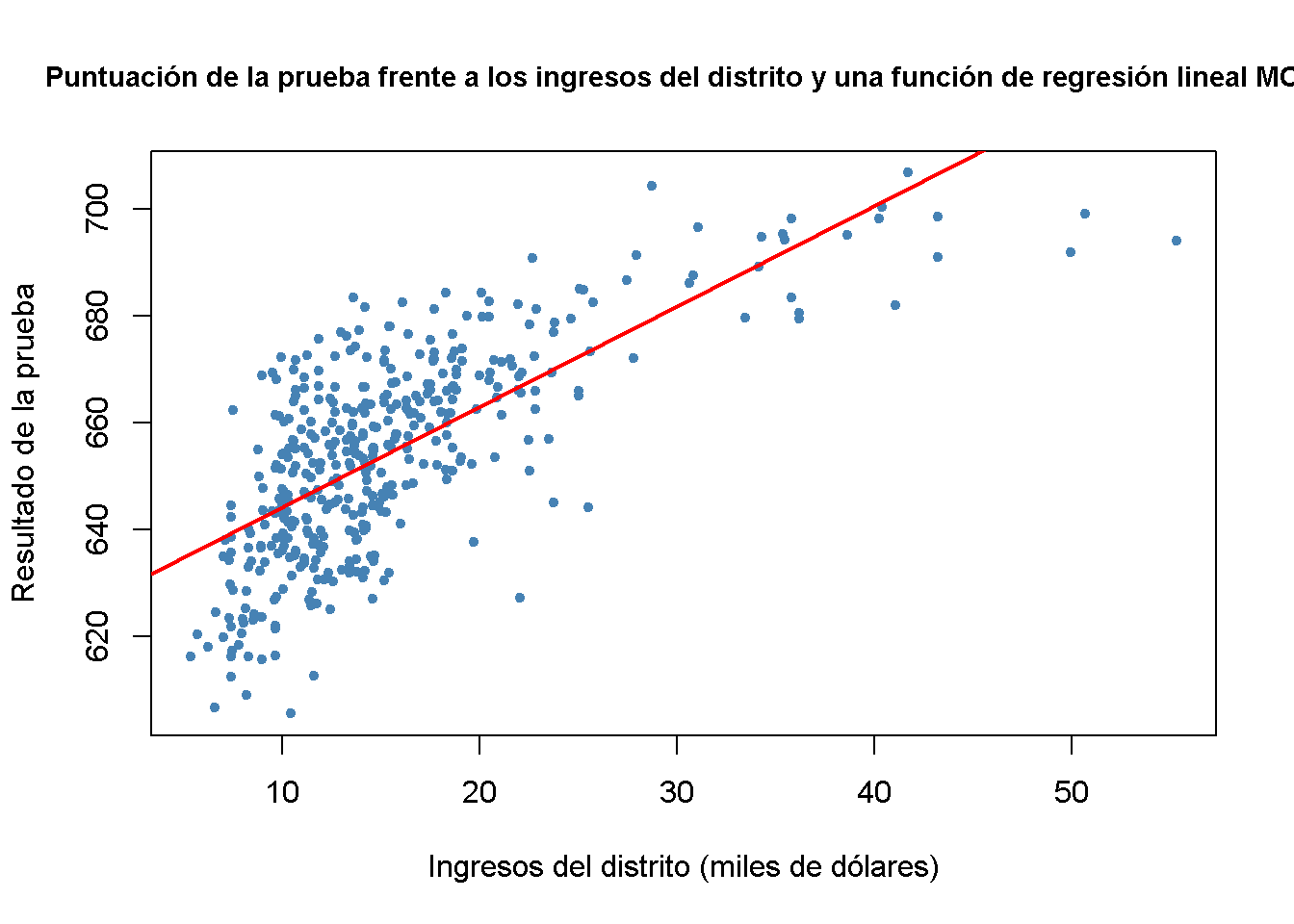
La línea de regresión lineal parece sobrestimar la verdadera relación cuando los ingresos son muy altos o muy bajos y la subestima para el grupo de ingresos medios.
Afortunadamente, MCO no solo maneja funciones lineales de los regresores. Por ejemplo, se pueden modelar las puntuaciones de las pruebas en función de los ingresos y el cuadrado de los ingresos. El modelo de regresión correspondiente es
\[TestScore_i = \beta_0 + \beta_1 \times income_i + \beta_2 \times income_i^2 + u_i,\] llamado modelo de regresión cuadrática; esto es, \(income^2\) se trata como una variable explicativa adicional. Por tanto, el modelo cuadrático es un caso especial de un modelo de regresión multivariante. Al ajustar el modelo con lm() se tiene que usar el operador ^ junto con la función I() para agregar el término cuadrático como un regresor adicional al argumento formula. Esto se debe a que la fórmula de regresión que se pasa por la función formula se convierte en un objeto de la clase formula. Para objetos de esta clase, los operadores +, -, y ^ tienen una interpretación no aritmética. I() garantiza que se utilicen como operadores aritméticos, consultar ?I,
# ajustar el modelo cuadrático
quadratic_model <- lm(score ~ income + I(income^2), data = CASchools)
# obtener el resumen del modelo
coeftest(quadratic_model, vcov. = vcovHC, type = "HC1")
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 607.3017435 2.9017544 209.2878 < 2.2e-16 ***
#> income 3.8509939 0.2680942 14.3643 < 2.2e-16 ***
#> I(income^2) -0.0423084 0.0047803 -8.8505 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La salida indica que la función de regresión estimada es
\[\widehat{TestScore}_i = \underset{(2.90)}{607.3} + \underset{(0.27)}{3.85} \times income_i - \underset{(0.0048)}{0.0423} \times income_i^2.\]
Este modelo permite probar la hipótesis de que la relación entre los puntajes de las pruebas y los ingresos del distrito es lineal frente a la alternativa de que es cuadrática. Esto corresponde a la prueba
\[H_0: \beta_2 = 0 \ \ \text{vs.} \ \ H_1: \beta_2\neq0,\]
ya que \(\beta_2=0\) corresponde a una ecuación lineal simple y \(\beta_2\neq0\) implica una relación cuadrática. Se encuentra que \(t=(\hat\beta_2 - 0)/SE(\hat\beta_2) = -0.0423/0.0048 = -8.81\), por lo que el valor de la hipótesis nula se rechaza en cualquier nivel común de significancia y se concluye que la relación no es lineal. Esto es consistente con la impresión obtenida de la gráfica.
Ahora se dibuja el mismo diagrama de dispersión que para el modelo lineal y se agrega la línea de regresión para el modelo cuadrático. Debido a que abline() solo puede dibujar líneas rectas, no se puede usar aquí. lines() es una función que permite dibujar líneas no rectas, ver ?lines. La llamada más básica de lines() es lines(x_values, y_values) donde x_values y y_values son vectores de misma longitud que proporcionan las coordenadas de los puntos que se conectarán secuencialmente por una línea. Esto hace que sea necesario ordenar los pares de coordenadas de acuerdo con los valores X. Aquí se usa la función order() para ordenar los valores ajustados de score de acuerdo con las observaciones de income.
# graficar un diagrama de dispersión de las observaciones para los ingresos y la puntuación de la prueba
plot(CASchools$income, CASchools$score,
col = "steelblue",
pch = 20,
xlab = "Ingresos del distrito (miles de dólares)",
ylab = "Resultado de la prueba",
main = "Funciones de regresión lineal y cuadrática estimadas")
# agregar una función lineal a la gráfica
abline(linear_model, col = "black", lwd = 2)
# agregar función cuadrática a la gráfica
order_id <- order(CASchools$income)
lines(x = CASchools$income[order_id],
y = fitted(quadratic_model)[order_id],
col = "red",
lwd = 2) 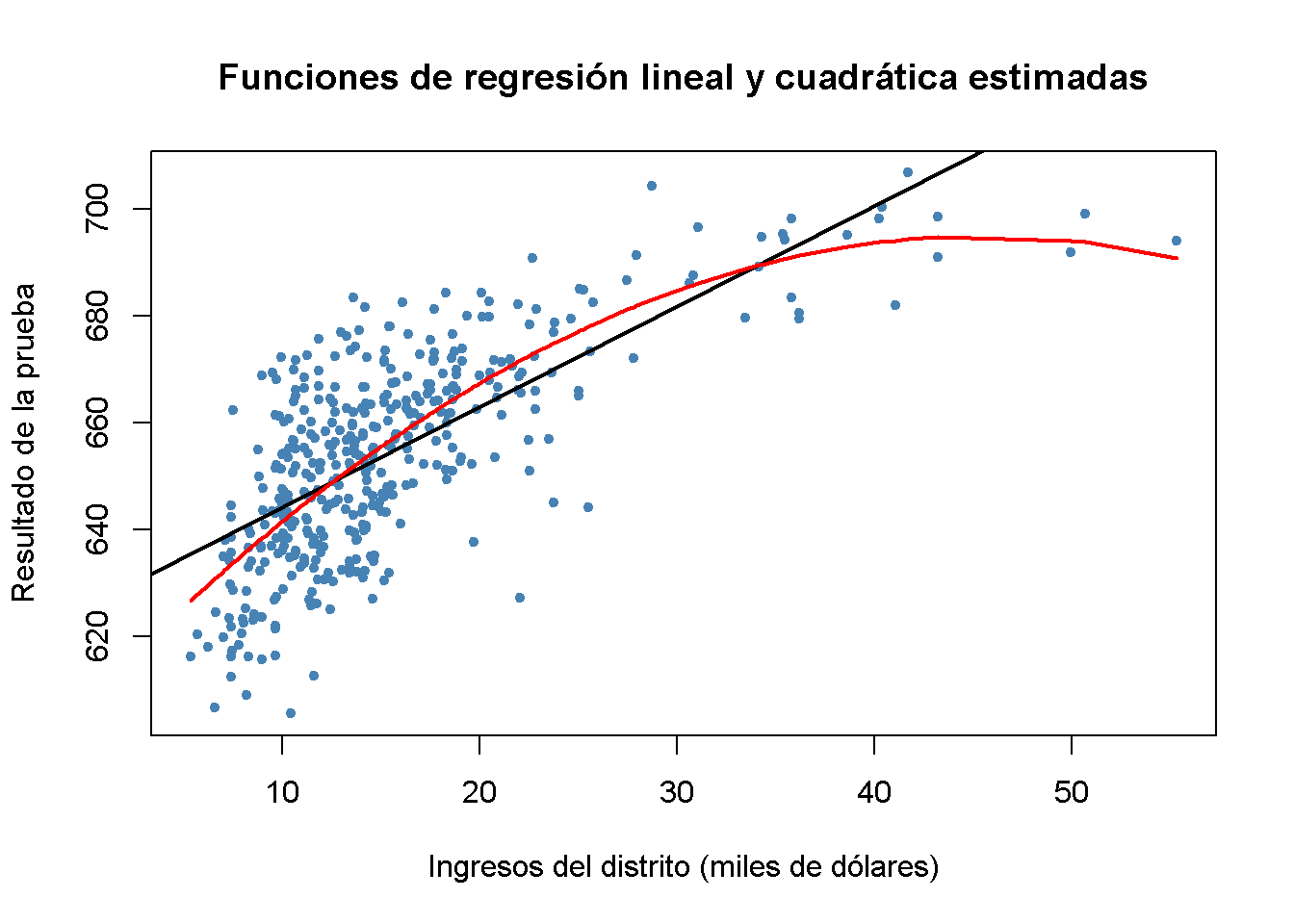
Se puede ver que la función cuadrática se ajusta a los datos mucho mejor que la función lineal.