6.1 Prueba de hipótesis de dos lados respecto al coeficiente de la pendiente
Usando el hecho de que \(\hat{\beta}_1\) se distribuye aproximadamente normalmente en muestras grandes (ver Concepto clave 4.4), se pueden probar hipótesis sobre el valor verdadero \(\beta_1\) como en el Capítulo 4.2.
Concepto clave 5.1
Forma general del estadístico \(t\)
Recuerde del Capítulo 4 que un estadístico \(t\) general tiene la forma
\[ t = \frac{\text{valor estimado} - \text{valor hipotético}}{\text{error estándar del estimador}}.\]
Concepto clave 5.2
Prueba de hipótesis sobre \(\beta_1\)
Para probar la hipótesis \(H_0: \beta_1 = \beta_{1,0}\), se deben realizar los siguientes pasos:
- Calcular el error estándar de \(\hat{\beta}_1\), \(SE(\hat{\beta}_1)\)
\[ SE(\hat{\beta}_1) = \sqrt{ \hat{\sigma}^2_{\hat{\beta}_1} } \ \ , \ \ \hat{\sigma}^2_{\hat{\beta}_1} = \frac{1}{n} \times \frac{\frac{1}{n-2} \sum_{i=1}^n (X_i - \overline{X})^2 \hat{u_i}^2 }{ \left[ \frac{1}{n} \sum_{i=1}^n (X_i - \overline{X})^2 \right]^2}. \]
- Calcular el estadístico \(t\)
\[ t = \frac{\hat{\beta}_1 - \beta_{1,0}}{ SE(\hat{\beta}_1) }. \]
- Dada una alternativa de dos lados (\(H_1:\beta_1 \neq \beta_{1,0}\)), se rechaza en el nivel \(5\%\) si \(|t^{act}| > 1.96\) o, de manera equivalente, si el valor de \(p\) es menor que \(0.05\).
Se debe recordar la definición del valor \(p\):
\[\begin{align*} p \text{-value} =& \, \text{Pr}_{H_0} \left[ \left| \frac{ \hat{\beta}_1 - \beta_{1,0} }{ SE(\hat{\beta}_1) } \right| > \left| \frac{ \hat{\beta}_1^{act} - \beta_{1,0} }{ SE(\hat{\beta}_1) } \right| \right] \\ =& \, \text{Pr}_{H_0} (|t| > |t^{act}|) \\ \approx& \, 2 \cdot \Phi(-|t^{act}|) \end{align*}\]
La última transformación se debe a la aproximación normal para muestras grandes.
Al considerar nuevamente la regresión MCO almacenada en linear_model del Capítulo 5 que dio la línea de regresión
\[\widehat{TestScore} \ = \underset{(9.47)}{698.9} - \underset{(0.49)}{2.28} \times STR \ , \ R^2=0.051 \ , \ SER=18.6.\]
Copie y ejecute el siguiente fragmento de código si el objeto de modelo anterior no está disponible en su entorno de trabajo.
# cargar el conjunto de datos `CASchools`
library(AER)
data(CASchools)
# agregar la proporción de alumnos por maestro
CASchools$STR <- CASchools$students/CASchools$teachers
# agregar puntaje promedio de prueba
CASchools$score <- (CASchools$read + CASchools$math)/2
# estimar el modelo
linear_model <- lm(score ~ STR, data = CASchools) Para probar una hipótesis sobre el parámetro de pendiente (el coeficiente de \(STR\)), se necesita \(SE(\hat{\beta}_1)\), el error estándar del estimador puntual respectivo. Como es común en la literatura, los errores estándar se presentan entre paréntesis debajo de las estimaciones puntuales.
El Concepto clave 5.1 revela que es bastante engorroso calcular el error estándar y, por lo tanto, el estadístico \(t\) a mano. La pregunta que debería hacerse ahora mismo es: ¿se pueden obtener estos valores con el mínimo esfuerzo utilizando R? Si se puede. Primero se usa summary() para obtener un resumen de los coeficientes estimados en linear_model.
Nota: A lo largo del curso, se informan errores estándar sólidos. Considere que es instructivo mantener las cosas simples al principio y, por lo tanto, comenzar con ejemplos simples que no permiten una inferencia sólida. Los errores estándar que son robustos a la heterocedasticidad se introducen en el Capítulo 6.4 donde se demuestra cómo se pueden calcular usando R. En el Capítulo 16 tiene lugar una discusión de los errores estándar robustos de heterocedasticidad-autocorrelación.
# imprimir el resumen de los coeficientes en la consola
summary(linear_model)$coefficients
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 698.932949 9.4674911 73.824516 6.569846e-242
#> STR -2.279808 0.4798255 -4.751327 2.783308e-06La segunda columna del resumen de los coeficientes informa \(SE(\hat\beta_0)\) y \(SE(\hat\beta_1)\). Además, en la tercera columna t value, se encuentra el estadístico \(t^{act}\) adecuado para las pruebas de hipótesis separadas \(H_0: \beta_0=0\) y \(H_0: \beta_1=0\). Además, la salida nos proporciona valores de \(p\) correspondientes a ambas pruebas frente a las alternativas de dos caras \(H_1:\beta_0\neq0\) respectivamente \(H_1:\beta_1\neq0\) en la cuarta columna de la tabla.
Es momento de echar un vistazo más de cerca a la prueba de
\[H_0: \beta_1=0 \ \ \ vs. \ \ \ H_1: \beta_1 \neq 0.\]
Se tiene que
\[ t^{act} = \frac{-2.279808 - 0}{0.4798255} \approx - 4.75. \]
¿Qué dice esto sobre la importancia del coeficiente estimado? Se rechaza la hipótesis nula en el nivel de significancia de \(5\%\) ya que \(|t^{act}| > 1.96\). Es decir, la estadística de prueba observada cae en la región de rechazo como \(p\text{-value} = 2.78\cdot 10^{-6} < 0.05\). Se concluye que el coeficiente es significativamente diferente de cero. En otras palabras, se rechaza la hipótesis de que el tamaño de la clase no influye en los resultados de las pruebas de los estudiantes al nivel de \(5\%\).
Tenga en cuenta que aunque la diferencia es insignificante en el presente caso, como se verá más adelante, summary() no realiza la aproximación normal, sino que calcula los valores de \(p\) usando la distribución \(t\) en su lugar. Generalmente, los grados de libertad de la distribución de \(t\) supuesta se determinan de la siguiente manera:
\[ \text{DF} = n - k - 1 \]
donde \(n\) es el número de observaciones utilizadas para estimar el modelo y \(k\) es el número de regresores, excluyendo la intersección. En este caso, se tienen \(n = 420\) observaciones y el único regresor es \(STR\) entonces \(k = 1\). La forma más sencilla de determinar los grados de libertad del modelo es
# determinar grados de libertad residuales
linear_model$df.residual
#> [1] 418Por lo tanto, para la distribución muestral asumida de \(\hat\beta_1\) se tienen
\[\hat\beta_1 \sim t_{418}\]
Tal que el valor \(p\) para una prueba de significancia bilateral se puede obtener ejecutando el siguiente código:
2 * pt(-4.751327, df = 418)
#> [1] 2.78331e-06El resultado está muy cerca del valor proporcionado por summary(). Sin embargo, dado que \(n\) es suficientemente grande, también se podría usar la densidad normal estándar para calcular el valor de \(p\):
2 * pnorm(-4.751327)
#> [1] 2.02086e-06De hecho, la diferencia es insignificante. Estos hallazgos indican que, si \(H_0: \beta_1 = 0\) es cierto y se tuviera que repetir todo el proceso de recopilar observaciones y estimar el modelo, ¡observar un \(\hat\beta_1 \geq |-2.28|\) es muy poco probable!
Usando R se puede visualizar cómo se hace tal declaración cuando se usa la aproximación normal. Esto refleja los principios descritos en el siguiente código, aunque es algo más largo que los ejemplos habituales y parece poco atractivo, pero hay mucha repetición, dado que se agregan matices de color y anotaciones en ambas colas de la distribución normal. Se debe recordar ejecutar el código paso a paso para ver cómo se aumenta el gráfico con las anotaciones.
# Graficar la normal estándar en el soporte [-6,6]
t <- seq(-6, 6, 0.01)
plot(x = t,
y = dnorm(t, 0, 1),
type = "l",
col = "steelblue",
lwd = 2,
yaxs = "i",
axes = F,
ylab = "",
main = expression("Cálculo del valor p de una prueba bilateral cuando "~t^act~" = -4.75"),
cex.lab = 0.7,
cex.main = 1)
tact <- -4.75
axis(1, at = c(0, -1.96, 1.96, -tact, tact), cex.axis = 0.7)
# sombrear las regiones críticas usando polygon():
# región crítica en la cola izquierda
polygon(x = c(-6, seq(-6, -1.96, 0.01), -1.96),
y = c(0, dnorm(seq(-6, -1.96, 0.01)), 0),
col = 'orange')
# región crítica en cola derecha
polygon(x = c(1.96, seq(1.96, 6, 0.01), 6),
y = c(0, dnorm(seq(1.96, 6, 0.01)), 0),
col = 'orange')
# Agregar flechas y textos que indiquen regiones críticas y el valor p
arrows(-3.5, 0.2, -2.5, 0.02, length = 0.1)
arrows(3.5, 0.2, 2.5, 0.02, length = 0.1)
arrows(-5, 0.16, -4.75, 0, length = 0.1)
arrows(5, 0.16, 4.75, 0, length = 0.1)
text(-3.5, 0.22,
labels = expression("0.025"~"="~over(alpha, 2)),
cex = 0.7)
text(3.5, 0.22,
labels = expression("0.025"~"="~over(alpha, 2)),
cex = 0.7)
text(-5, 0.18,
labels = expression(paste("-|",t[act],"|")),
cex = 0.7)
text(5, 0.18,
labels = expression(paste("|",t[act],"|")),
cex = 0.7)
# Agregar palos que indiquen valores críticos en el nivel 0.05, t^act y -t^act
rug(c(-1.96, 1.96), ticksize = 0.145, lwd = 2, col = "darkred")
rug(c(-tact, tact), ticksize = -0.0451, lwd = 2, col = "darkgreen")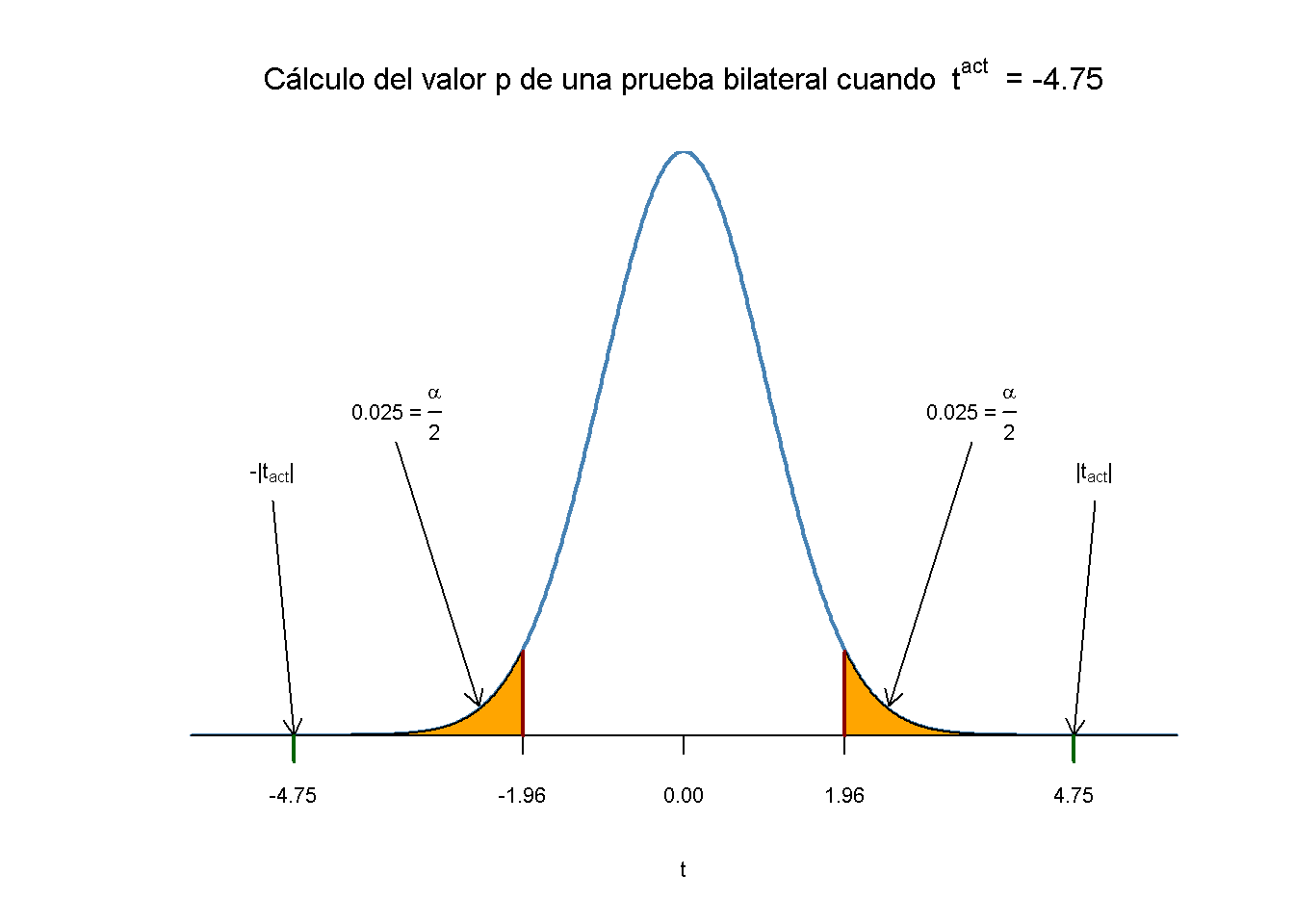
El valor \(p\) es el área bajo la curva a la izquierda de \(-4.75\) más el área bajo la curva a la derecha de \(4.75\). Como ya se sabe por los cálculos anteriores, este valor es muy pequeño.