6.6 Uso del estadístico t en regresión cuando el tamaño de la muestra es pequeño
Los tres supuestos de MCO discutidos en el Capítulo 5 (ver Concepto clave 4.3) son la base de los resultados de la distribución muestral grande de los estimadores de MCO en el modelo de regresión simple. ¿Qué se puede decir acerca de la distribución de los estimadores y sus estadísticos \(t\) cuando el tamaño de la muestra es pequeño y se desconoce la distribución poblacional de los datos? Siempre que se cumplan los tres supuestos de mínimos cuadrados y los errores estén distribuidos normalmente y sean homocedásticos (se hace referecnia a estas condiciones como supuestos de regresión normal homocedásticos), se tienen estimadores distribuidos normalmente y estadísticos de prueba distribuidos en \(t\) en muestras pequeñas.
Recuerde la definición de una variable distribuida \(t\)
\[\frac{Z}{\sqrt{W/M}}\sim t_M\]
donde \(Z\) es una variable aleatoria normal estándar, \(W\) es \(\chi^2\) distribuida con \(M\) grados de libertad y \(Z\) y \(W\) son independientes. Ejemplo de la distribución muestral pequeña del estadístico \(t\) en los métodos de regresión.
Simulando la distribución de los estadísticos de regresión \(t\) basados en un gran número de pequeñas muestras aleatorias, suponiendo \(n = 20\), y comparando las distribuciones simuladas con las distribuciones teóricas que deberían ser \(t_{18}\), la distribución \(t\) con \(18\) grados de libertad (recuerde que \(\text{DF} = nk-1\)).
# inicializar dos vectores
beta_0 <- c()
beta_1 <- c()
# muestreo de bucle/estimación/estadístico t
for (i in 1:10000) {
X <- runif(20, 0, 20)
Y <- rnorm(n = 20, mean = X)
reg <- summary(lm(Y ~ X))
beta_0[i] <- (reg$coefficients[1, 1] - 0)/(reg$coefficients[1, 2])
beta_1[i] <- (reg$coefficients[2, 1] - 1)/(reg$coefficients[2, 2])
}
# graficar las distribuciones y comparar con la densidad t_18:
# dividir el área del gráfico
par(mfrow = c(1, 2))
# graficar la densidad simulada de beta_0
plot(density(beta_0),
lwd = 2 ,
main = expression(widehat(beta)[0]),
xlim = c(-4, 4))
# agregar la densidad t_18 al gráfico
curve(dt(x, df = 18),
add = T,
col = "red",
lwd = 2,
lty = 2)
# graficar la densidad simulada de beta_1
plot(density(beta_1),
lwd = 2,
main = expression(widehat(beta)[1]), xlim = c(-4, 4)
)
# agregar la densidad t_18 al gráfico
curve(dt(x, df = 18),
add = T,
col = "red",
lwd = 2,
lty = 2) 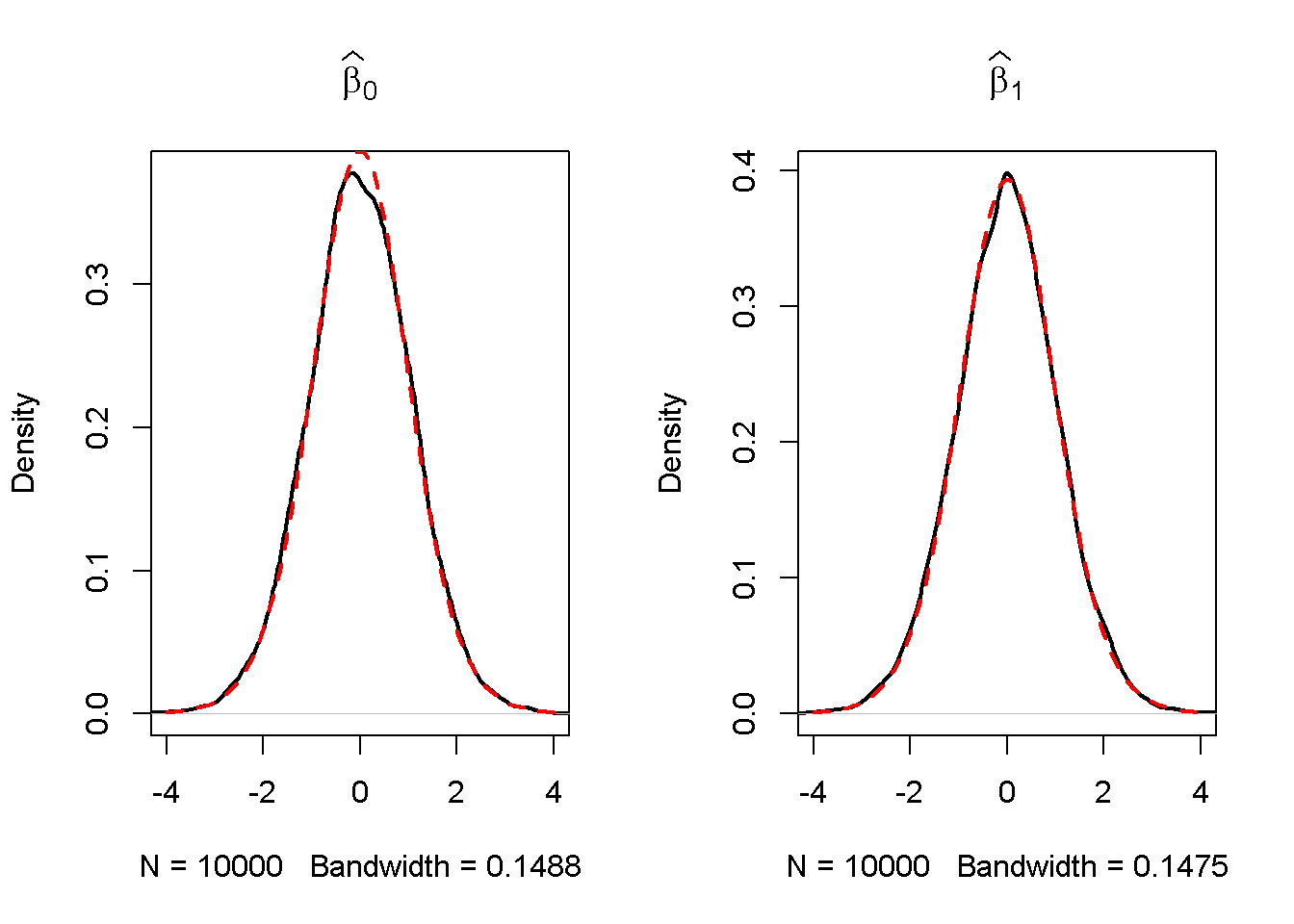
Los resultados son consistentes con las expectativas: Las distribuciones empíricas de ambos estimadores parecen seguir la distribución teórica \(t_{18}\) bastante de cerca.