4.1 Estimación de la media poblacional

Concepto clave 3.1

Estimadores y estimaciones

Los estimadores son funciones extraídas de una muestra de datos que parten de una población desconocida. Las estimaciones son valores numéricos calculados por estimadores basados en los datos de la muestra. Los estimadores son variables aleatorias porque son funciones de datos aleatorios. Las estimaciones son números no aleatorios.

Piense en alguna variable económica, por ejemplo, los ingresos por hora de los graduados universitarios, denotados por $Y$. Suponga que se está interesado en $\mu_Y$ la media de $Y$. Para calcular exactamente $\mu_Y$ se tendrían que entrevistar a todos los graduados que trabajan en el sistema económico. Simplemente no se puede hacer esto debido a limitaciones de tiempo y costos. Sin embargo, se puede extraer una muestra aleatoria de $n$ i.i.d. observaciones $Y_1, \dots, Y_n$ y estimar $\mu_Y$ usando uno de los estimadores más simples en el sentido del Concepto Clave 3.1 que uno pueda imaginar, es decir,

$$\overline{Y} = \frac{1}{n} \sum_{i=1}^n Y_i,$$

la media muestral de $Y$. Por otra parte, se podría usar un estimador aún más simple para $\mu_Y$: la primera observación de la muestra, $Y_1$. ¿Es $Y_1$ un buen estimador? Por ahora, asuma que

$$Y \sim \chi_{12}^2$$

lo cual no es demasiado irracional ya que los ingresos por hora no son negativos y se espera que muchas ganancias por hora estén en un rango de $5€\,$ a $15€$. Además, es común que las distribuciones de ingresos estén sesgadas hacia la derecha, una propiedad de la distribución $\chi^2_{12}$.

# graficar la distribución chi_12^2
curve(dchisq(x, df=12), 
      from = 0, 
      to = 40, 
      ylab = "Densidad", 
      xlab = "Ganancias por hora en euros")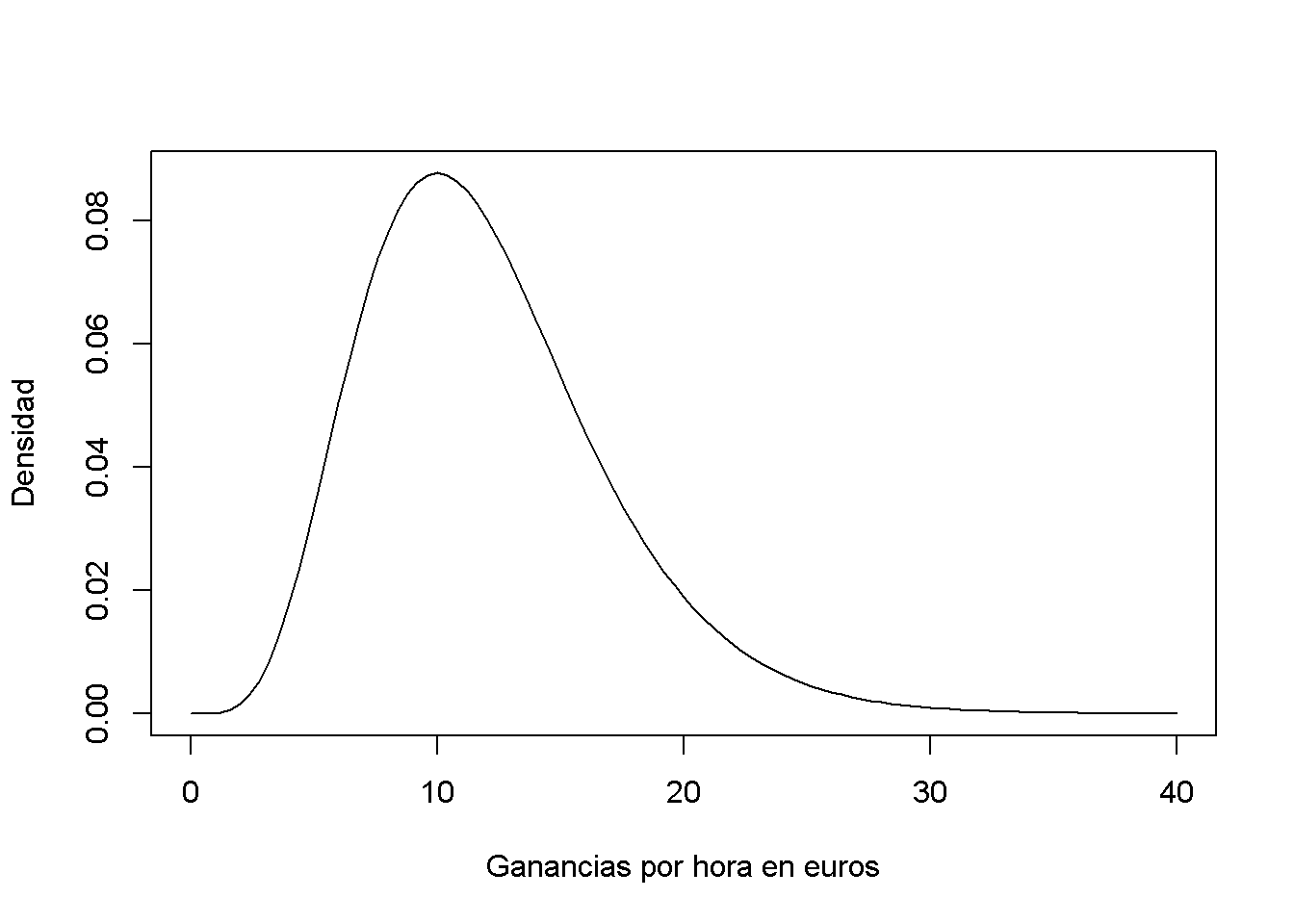

Ahora se extraerá una muestra de $n = 100$ observaciones y se tomará la primera observación $Y_1$ como una estimación de $\mu_Y$

# sembrar la semilla para la reproducibilidad
set.seed(1)

# muestra de la distribución chi_12^2, usar solo la primera observación
rsamp <- rchisq(n = 100, df = 12)
rsamp[1]
#> [1] 8.257893

El estimado de $8.26$ no está muy lejos de $\mu_Y = 12$ pero es algo intuitivo que se podría hacer algo mejor: el estimador $Y_1$ descarta mucha información y su varianza es la varianza de la población:

$$\text{Var}(Y_1) = \text{Var}(Y) = 2 \cdot 12 = 24$$

Esto nos lleva a la siguiente pregunta: ¿Qué es un estimador bueno de un parámetro desconocido en primer lugar? Esta cuestión se aborda en los Conceptos clave 3.2 y 3.3.

Concepto clave 3.2

Sesgo, consistencia y eficiencia

Las características deseables de un estimador incluyen insesgabilidad, consistencia y eficiencia.

Insesgabilidad:

Si la media de la distribución muestral de algún estimador $\hat\mu_Y$ para la media poblacional $\mu_Y$ es igual a $\mu_Y$,

$$E(\hat\mu_Y) = \mu_Y,$$

el estimador es imparcial para $\mu_Y$. El sesgo de $\hat\mu_Y$ entonces es $0$:

$$E(\hat\mu_Y) - \mu_Y = 0$$

Consistencia:

Se quiere que la incertidumbre del estimador $\mu_Y$ disminuya a medida que aumenta el número de observaciones en la muestra. Más precisamente, se quiere que la probabilidad de que la estimación $\hat\mu_Y$ caiga dentro de un pequeño intervalo alrededor del valor real $\mu_Y$ se acerque cada vez más a $1$ a medida que $n$ crece. Se escribe esto como

$$\hat\mu_Y \xrightarrow{p} \mu_Y.$$

Varianza y eficiencia:

Se quiere que el estimador sea eficiente. Suponga que se tienen dos estimadores, $\hat\mu_Y$ y $\overset{\sim}{\mu}_Y$ para un tamaño de muestra dado $n$ se sigue que

$$E(\hat\mu_Y) = E(\overset{\sim}{\mu}_Y) = \mu_Y$$

pero

$$\text{Var}(\hat\mu_Y) < \text{Var}(\overset{\sim}{\mu}_Y).$$

Entonces se prefiere usar $\hat\mu_Y$, ya que tiene una variación menor que $\overset{\sim}{\mu}_Y$, lo que significa que $\hat\mu_Y$ es más eficiente en el uso de la información proporcionada por las observaciones en la muestra.