5.1 Regresión lineal simple
Para comenzar con un ejemplo sencillo, considere las siguientes combinaciones de puntaje promedio de exámenes y la proporción promedio de estudiantes por maestro en algunos distritos escolares ficticios.
Para trabajar con estos datos en R, se comienza generando dos vectores: uno para las proporciones alumno-maestro (STR) y otro para los puntajes de las pruebas (TestScore), ambos contienen los datos de la tabla de arriba.
# Crear datos de muestra
STR <- c(15, 17, 19, 20, 22, 23.5, 25)
TestScore <- c(680, 640, 670, 660, 630, 660, 635)
# Imprimir datos de muestra
STR
#> [1] 15.0 17.0 19.0 20.0 22.0 23.5 25.0
TestScore
#> [1] 680 640 670 660 630 660 635Para construir un modelo de regresión lineal simple, se plantea la hipótesis de que la relación entre la variable dependiente y la independiente es lineal, formalmente:
\[ Y = b \cdot X + a. \]
Por ahora, suponga que la función que relaciona la puntuación de la prueba y la proporción alumno-maestro entre sí es \[TestScore = 713 - 3 \times STR.\]
Siempre es una buena idea visualizar los datos con los que trabaja. Aquí, es adecuado usar plot() para producir un diagrama de dispersión con STR en el eje \(x\) y TestScore en el eje \(y\). Simplemente llamando a plot(y_variable ~ x_variable) donde y_variable y x_variable son marcadores de posición para los vectores de observaciones que se quiere trazar. Además, es posible que se desee agregar una relación sistemática a la trama. Para dibujar una línea recta, R proporciona la función abline(). Solo se tiene que llamar a la función con el argumento a (que representan la intersección) y b (que representa la pendiente) después de ejecutar plot() para agregar la línea al gráfico.
El siguiente código es clave:
# crear un diagrama de dispersión de los datos
plot(TestScore ~ STR)
# agregar la relación sistemática a la trama
abline(a = 713, b = -3)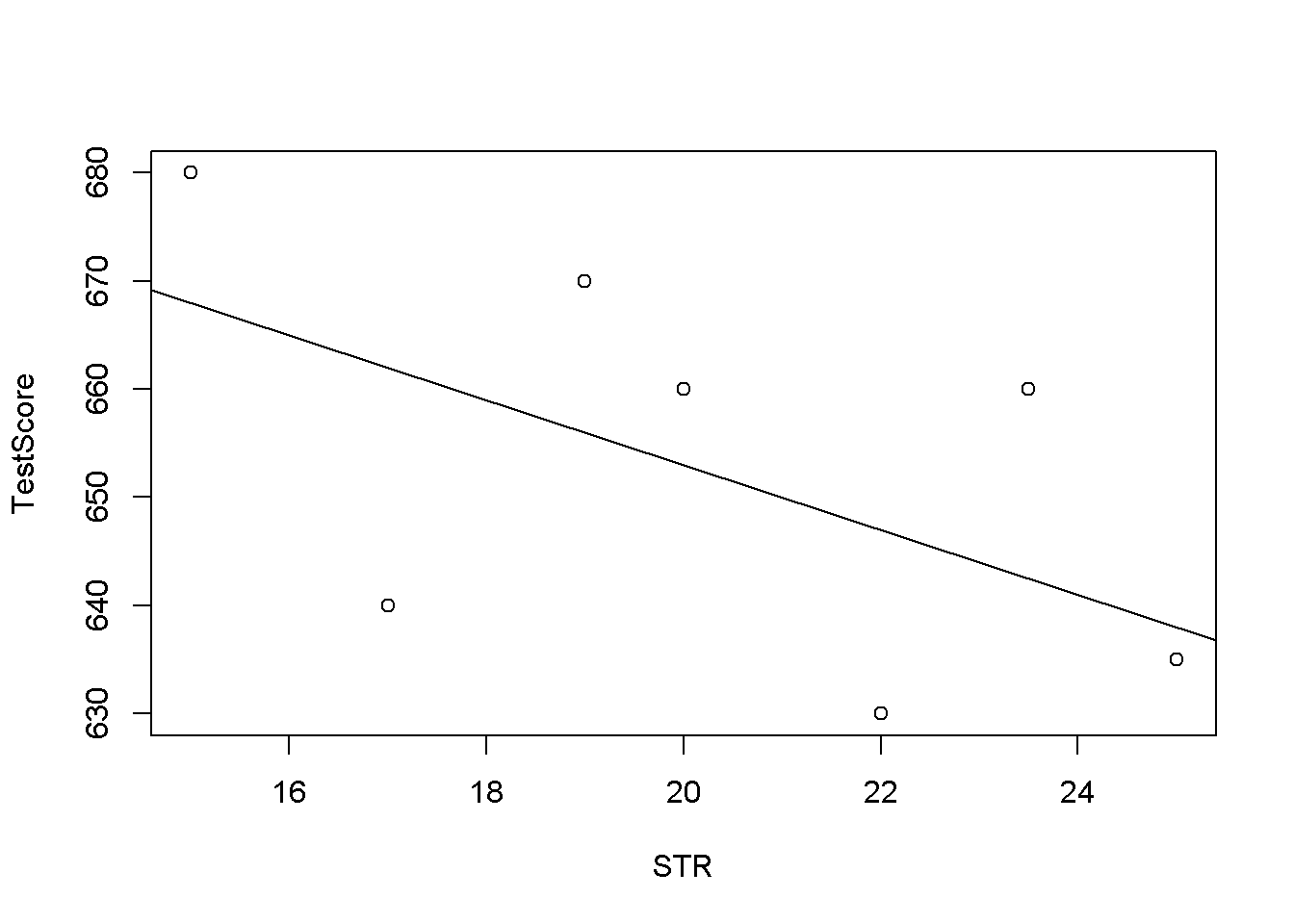
Se encuentra que la línea no toca ninguno de los puntos aunque se afirma que representa la relación sistemática. La razón de esto es la aleatoriedad. La mayoría de las veces existen influencias adicionales que implican que no existe una relación bivariada entre las dos variables.
Para tener en cuenta dichas diferencias entre los datos observados y la relación sistemática, se amplía el modelo de arriba con un término de error \(u\) que captura efectos aleatorios adicionales. Dicho de otra manera, \(u\) representa todas las diferencias entre la línea de regresión y los datos observados reales. Además de la pura aleatoriedad, estas desviaciones también podrían surgir de errores de medición o, como se discutirá más adelante, podrían ser la consecuencia de dejar de lado otros factores que son relevantes para explicar la variable dependiente.
¿Qué otros factores son plausibles en el ejemplo? Por un lado, los puntajes de las pruebas pueden depender de la calidad de los profesores y los antecedentes de los estudiantes. También es posible que en algunas clases los alumnos tuvieran suerte en los días de prueba y así consiguieran puntuaciones más altas. Por ahora, se resumiran tales influencias por un componente aditivo:
\[ TestScore = \beta_0 + \beta_1 \times STR + \text{other factors} \]
Por supuesto, esta idea es muy general, ya que se puede extender fácilmente a otras situaciones que se pueden describir con un modelo lineal. Por tanto, el modelo de regresión lineal básico con el que se trabajará es
\[ Y_i = \beta_0 + \beta_1 X_i + u_i. \]
El Concepto clave 4.1 resume la terminología del modelo de regresión lineal simple.
Concepto clave 4.1
Terminología para el modelo de regresión lineal con un regresor único
El modelo de regresión lineal es
\[Y_i = \beta_0 + \beta_1 X_i + u_i\]
dónde
- el índice \(i\) corre sobre las observaciones, \(i = 1, \dots, n\).
- \(Y_i\) es la variable dependiente, la regresiva, o simplemente la variable de la izquierda.
- \(X_i\) es la variable independiente, el regresor, o simplemente la variable de la derecha.
- \(Y = \beta_0 + \beta_1 X\) es la línea de regresión de población también llamada función de regresión de población.
- \(\beta_0\) es la intersección de la línea de regresión de la población.
- \(\beta_1\) es la pendiente de la línea de regresión de la población.
- \(u_i\) es el término de error.