17.4 Agrupación de volatilidad y heterocedasticidad condicional autorregresiva
Las series de tiempo financieras suelen presentar un comportamiento que se conoce como agrupamiento de volatilidad: La volatilidad cambia con el tiempo y su grado muestra una tendencia a persistir; es decir, existen periodos de baja volatilidad y periodos donde la volatilidad es alta. Los econometristas llaman a esto heterocedasticidad condicional autorregresiva. La heterocedasticidad condicional es una propiedad interesante porque puede explotarse para pronosticar la varianza de períodos futuros.
Como ejemplo, se consideran los cambios diarios en el índice bursátil Whilshire 5000. Los datos están disponibles para su descarga en la Base de datos económicos de la Reserva Federal. Para mantener la coherencia con el libro, se descargaron los datos desde el 29 de diciembre de 1989 hasta el 31 de diciembre de 2013 (es necesario elegir este intervalo de tiempo algo mayor, ya que más adelante se trabajará con los cambios diarios de la serie).
El siguiente fragmento de código muestra cómo formatear los datos y crear un gráfico a partir de ellos.
# importar datos del índice Wilshire 5000
W5000 <- read.csv2("data/Wilshire5000.csv",
stringsAsFactors = F,
header = T,
sep = ",",
na.strings = ".")
# transformar las columnas
W5000$DATE <- as.Date(W5000$DATE)
W5000$WILL5000INDFC <- as.numeric(W5000$WILL5000INDFC)
# eliminar NAs
W5000 <- na.omit(W5000)
# calcular cambios porcentuales diarios
W5000_PC <- data.frame("Date" = W5000$DATE,
"Value" = as.numeric(Delt(W5000$WILL5000INDFC) * 100))
W5000_PC <- na.omit(W5000_PC)# graficar cambios porcentuales
plot(W5000_PC,
ylab = "Porcentaje",
main = "Cambios porcentuales diarios",
type="l",
col = "steelblue",
lwd = 0.5)
# agregar una línea horizontal en y = 0
abline(0, 0)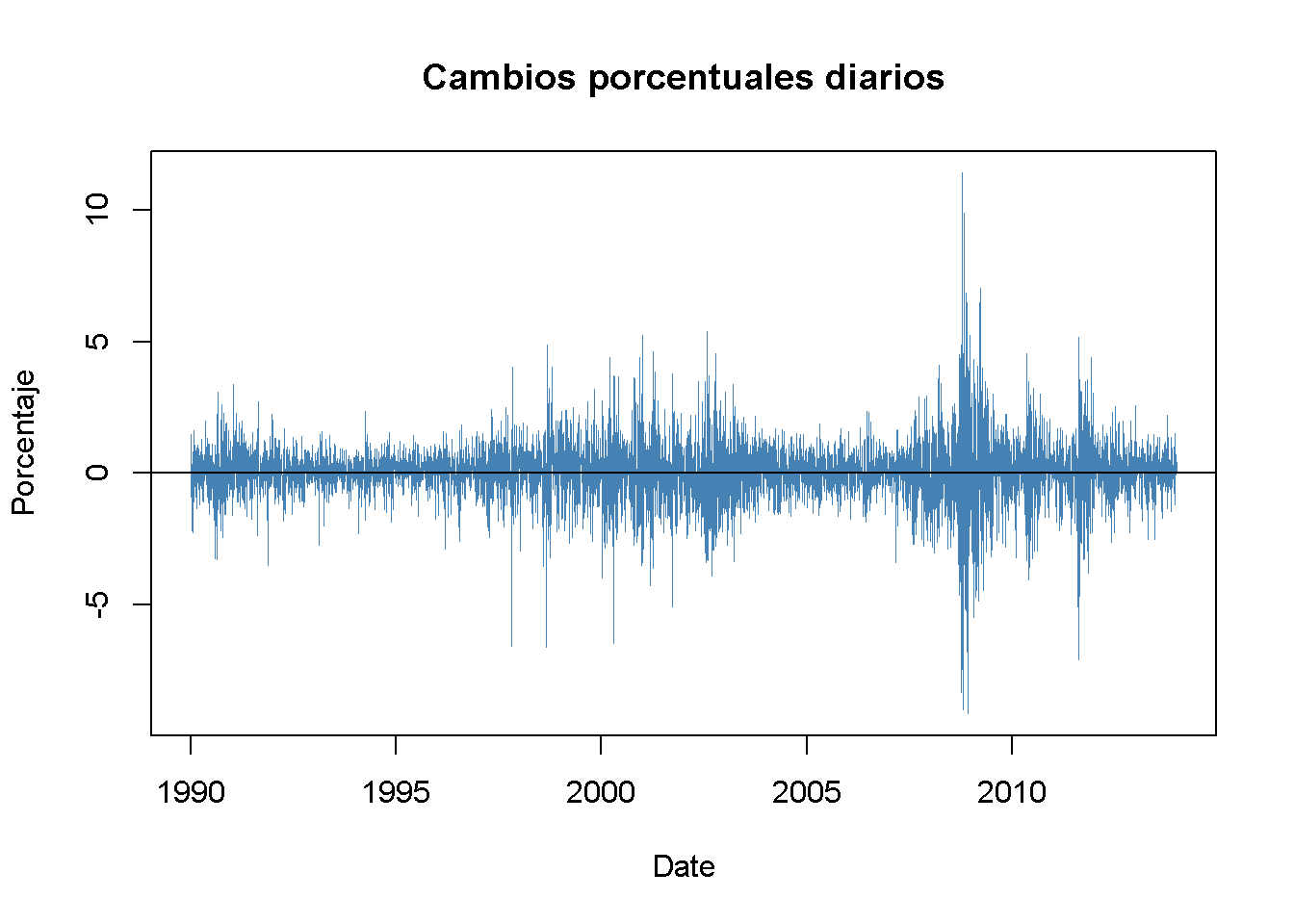
(#fig:pcw5000, 914)Rendimientos porcentuales diarios en el índice Wilshire 5000
La serie de cambios porcentuales diarios en el índice de Wilshire parece fluctuar aleatoriamente alrededor de cero, lo que significa que existe poca autocorrelación. Esto se confirma mediante un gráfico de la función de autocorrelación de la muestra.
# graficar la autocorrelación de la muestra de los cambios porcentuales diarios
acf(W5000_PC$Value, main = "Serie 5000 de Wilshire")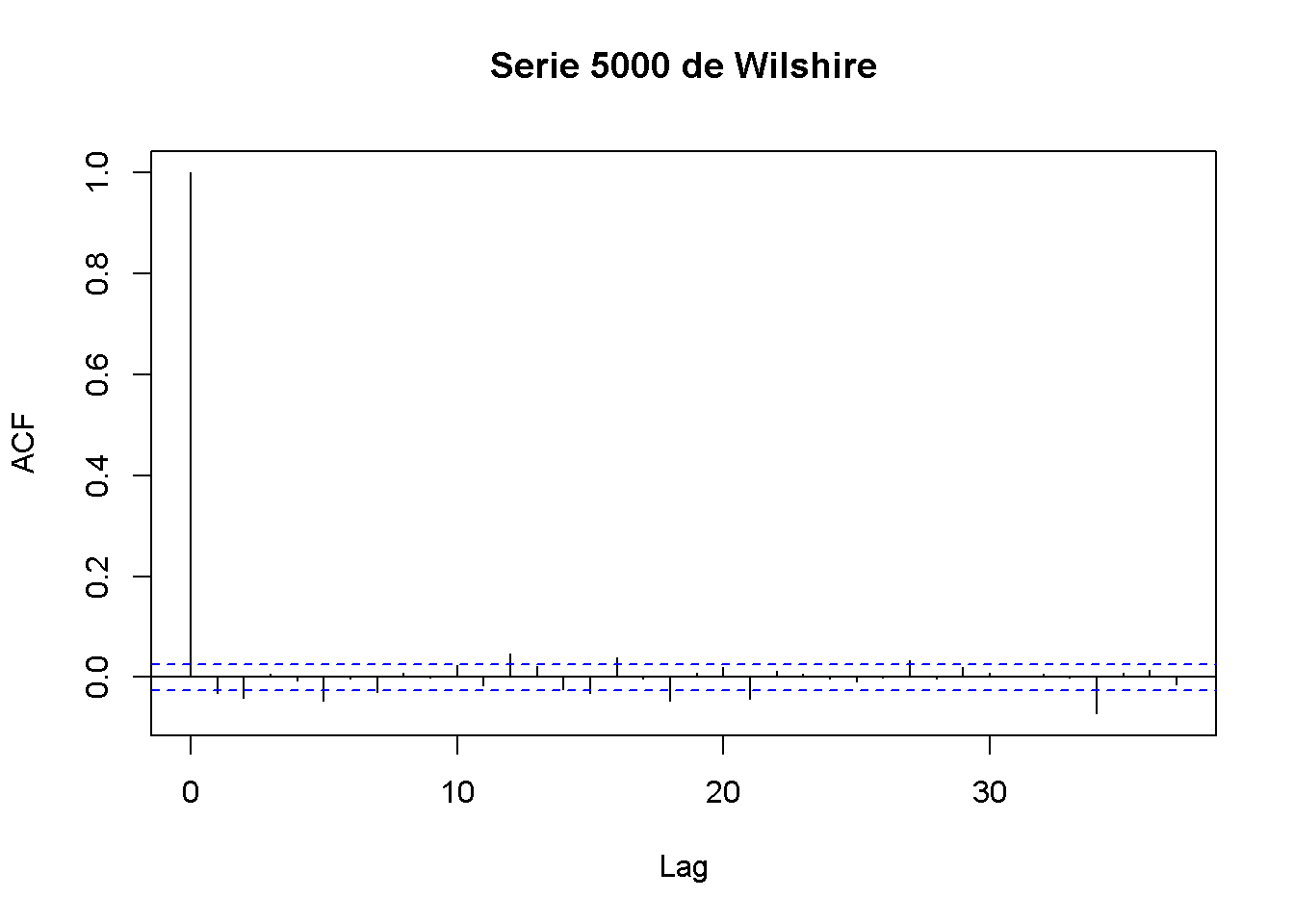
(#fig:acfw5000, 915)Autocorrelación en los cambios diarios de precios del índice W5000
En la Figura ?? se ve que las autocorrelaciones son bastante débiles, por lo que es difícil predecir los resultados futuros utilizando, por ejemplo, un modelo AR.
Sin embargo, existe evidencia visual en ?? de que la serie de retornos exhibe heterocedasticidad condicional, ya que se observan agrupaciones de volatilidad. Para algunas aplicaciones, es útil medir y pronosticar estos patrones. Esto se puede hacer utilizando modelos que asumen que la volatilidad puede describirse mediante un proceso autorregresivo.
Modelos ARCH y GARCH
Considere \[Y_t = \beta_0 + \beta_1 Y_{t-1} + \gamma_1 X_{t-1} + u_t,\] un modelo de regresión ADL(\(1\),\(1\)). El econométrico Robert Engle (1982) propuso modelar \(\sigma^2_t = Var(u_t | u_{t-1},u_{t-2},\ldots)\), la varianza condicional del error \(u_t\) dado su pasado, por un modelo de retraso distribuido de orden \(p\),
\[\begin{align} \sigma^2_t = \alpha_0 + \alpha_1 u_{t-1}^2 + \alpha_2 u_{t-2}^2 + \dots + \alpha_p u_{t-p}^2, \tag{17.1} \end{align}\]
llamado modelo de heterocedasticidad condicional autorregresiva (ARCH) de orden \(p\), o ARCH corto (\(p\)).2 Se supone \(\alpha_0>0\) y \(\alpha_1,\ldots,\alpha_p\geq0\) para asegurar una varianza positiva \(\sigma_t^2>0\). La idea general se desprende de la estructura del modelo: Los coeficientes positivos \(\alpha_0,\alpha_1,\dots,\alpha_p\) implican que los grandes errores cuadrados recientes conducen a una gran varianza y, por lo tanto, a grandes errores cuadrados en el período actual.
El modelo ARCH generalizado (GARCH), desarrollado por Tim Bollerslev (1986), es una extensión del modelo ARCH, donde se permite que \(\sigma^2_t\) dependa de sus propios retrasos y de los retrasos del término de error al cuadrado. El modelo GARCH (\(p\),\(q\)) viene dado por
\[\begin{align} \sigma^2_t = \alpha_0 + \alpha_1 u_{t-1}^2 + \alpha_2 u_{t-2}^2 + \dots + \alpha_p u_{t-p}^2 + \phi_1 \sigma^2_{t-1} + \dots + \phi_p \sigma^2_{t-q}. \tag{17.2} \end{align}\]
El modelo GARCH es un modelo ADL (\(p\),\(q\)) y, por lo tanto, puede proporcionar parametrizaciones más parsimoniosas que el modelo ARCH.
Aplicación a la volatilidad del precio de las acciones
Las estimaciones de máxima verosimilitud de los modelos ARCH y GARCH son eficientes y tienen distribuciones normales en muestras grandes, de modo que se pueden aplicar los métodos habituales para realizar inferencias sobre los parámetros desconocidos. El paquete fGarch en R consiste en una colección de funciones para analizar y modelar el comportamiento heterocedástico en modelos de series de tiempo. La función garchFit() es algo sofisticada, dado que permite diferentes especificaciones del procedimiento de optimización, diferentes distribuciones de errores y mucho más (use ?GarchFit para una descripción detallada de los argumentos). En particular, los errores estándar reportados por garchFit() son robustos.
El modelo GARCH (\(1\),\(1\)) de cambios diarios en el índice Wilshire 5000 que se estimó viene dado por:
\[\begin{align} R_t =& \, \beta_0 + u_t \ , \ u_t \sim \mathcal{N}(0,\sigma^2_t), \\ \sigma^2_t =& \, \alpha_0 + \alpha_1 u_{t-1}^2 + \phi_1 \sigma_{t-1}^2 \tag{17.3} \end{align}\]
donde \(R_t\) es el cambio porcentual en el período \(t\). \(\beta_0\), \(\alpha_0\), \(\alpha_1\) y \(\phi_1\) son coeficientes desconocidos y \(u_t\) es un término de error con media condicional cero. No se incluyen predictores rezagados en la ecuación de \(R_t\) porque los cambios diarios en el índice Wilshire 5000 reflejan rendimientos bursátiles diarios que son esencialmente impredecibles. Se debe tener en cuenta que se supone que \(u_t\) tiene una distribución normal y la varianza \(\sigma^2_t\) depende de \(t\), ya que sigue la recursividad GARCH (\(1\),\(1\)) (17.3).
Es sencillo estimar este modelo usando garchFit().
# estimar el modelo GARCH (1,1) de cambios porcentuales diarios
GARCH_Wilshire <- garchFit(data = W5000_PC$Value, trace = F)Se obtiene:
\[\begin{align} \widehat{R}_t =& \, \underset{(0.010)}{0.068}, \tag{17.4} \\ \widehat{\sigma}^2_t =& \, \underset{(0.002)}{0.011} + \underset{(0.007)}{0.081} u_{t-1}^2 + \underset{(0.008)}{0.909} \sigma_{t-1}^2, \tag{17.5} \end{align}\]
por lo que los coeficientes en \(u_{t-1}^2\) y \(\sigma^2_{t-1}\) son estadísticamente significativos en cualquier nivel común de significancia. Se puede demostrar que la persistencia de movimientos en \(\sigma^2_t\) está determinada por la suma de ambos coeficientes, que aquí es \(0.99\). Esto indica que los movimientos en la varianza condicional son muy persistentes, lo que implica períodos prolongados de alta volatilidad, lo que es consistente con la evidencia visual de la agrupación de volatilidad presentada anteriormente.
La varianza condicional estimada \(\widehat{\sigma}^2_t\) se puede calcular conectando los residuos de (17.4) en la ecuación (17.5). Esto lo realiza automáticamente garchFit(), por lo que para obtener las desviaciones estándar condicionales estimadas \(\widehat{\sigma}_t\) solo se tienen que leer los valores de GARCH_Wilshire agregando \(\textit{@sigma.t}\).
Usando \(\widehat{\sigma}_t\) se grafican bandas de \(\pm\) una desviación estándar condicional junto con las desviaciones de la serie de cambios porcentuales diarios en el índice Wilshire 5000 de su media. El siguiente fragmento de código genera el gráfico.
# calcular las desviaciones de los cambios porcentuales de su media
dev_mean_W5000_PC <- W5000_PC$Value - GARCH_Wilshire@fit$coef[1]
# graficar la desviación de los cambios porcentuales de la media
plot(W5000_PC$Date, dev_mean_W5000_PC,
type = "l",
col = "steelblue",
ylab = "Porcentaje",
xlab = "Fecha",
main = "Bandas estimadas de + - una desviación estándar condicional",
lwd = 0.2)
# agregar una línea horizontal en y = 0
abline(0, 0)
# agregar bandas de confianza GARCH(1,1) (una desviación estándar) al gráfico
lines(W5000_PC$Date,
GARCH_Wilshire@fit$coef[1] + GARCH_Wilshire@sigma.t,
col = "darkred",
lwd = 0.5)
lines(W5000_PC$Date,
GARCH_Wilshire@fit$coef[1] - GARCH_Wilshire@sigma.t,
col = "darkred",
lwd = 0.5)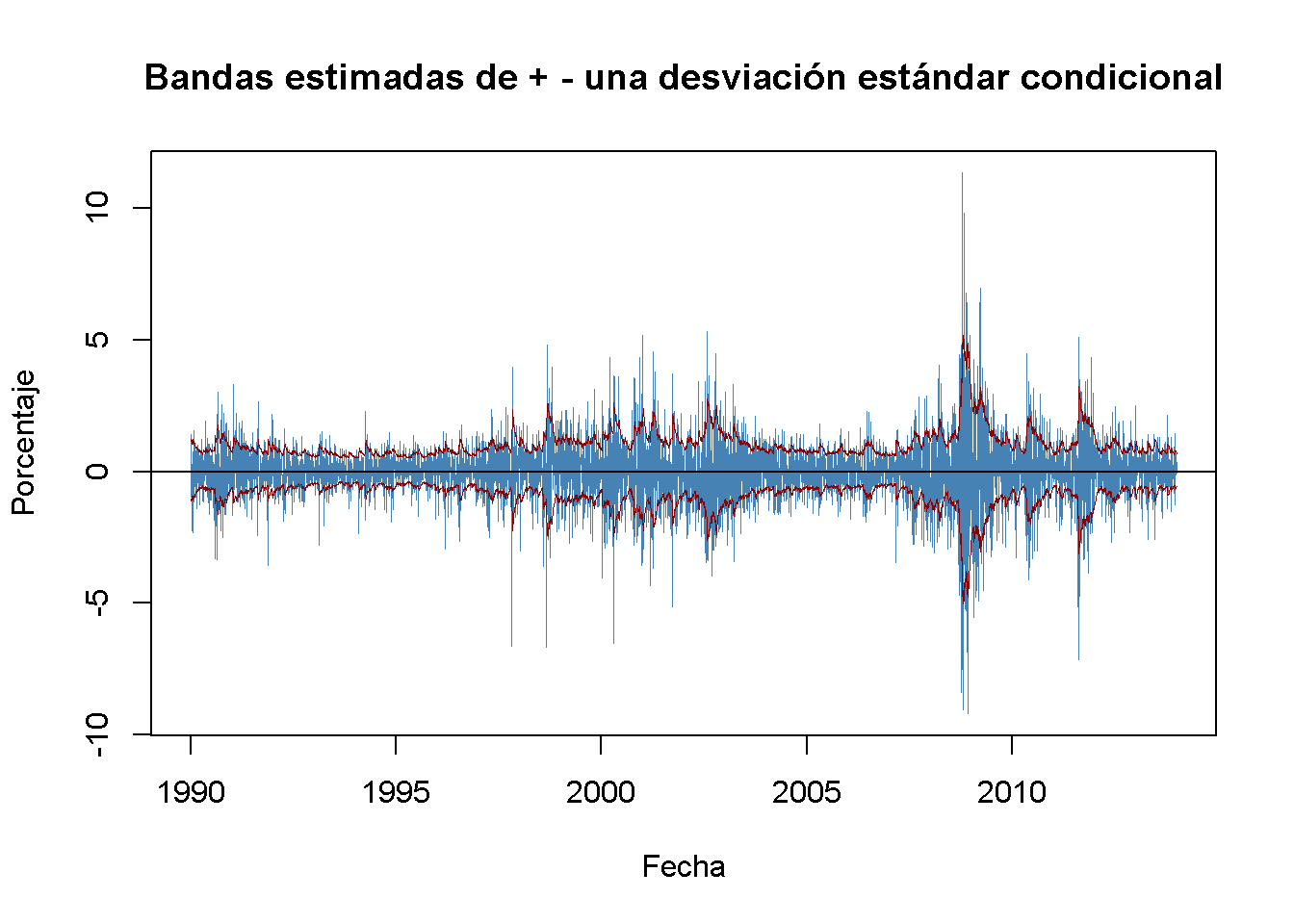
Las bandas de las desviaciones estándar condicionales estimadas siguen bastante bien la heterocedasticidad observada en la serie de cambios diarios del índice Wilshire 5000. Esto es útil para cuantificar la volatilidad variable en el tiempo y el riesgo resultante para los inversores que poseen acciones resumidas por el índice. Además, este modelo GARCH también se puede utilizar para producir intervalos de pronóstico cuyos anchos dependen de la volatilidad de los períodos más recientes.
Resumen
Se ha discutido cómo las autorregresiones vectoriales se estiman convenientemente y se usan para pronosticar en R mediante funciones del paquete vars.
El paquete urca proporciona métodos avanzados para el análisis de la raíz unitaria y cointegración como las pruebas DF-GLS y EG-ADF. En una aplicación, se ha encontrado evidencia de que las tasas de interés a 3 meses y 10 años tienen una tendencia estocástica común (es decir, están cointegradas) y, por lo tanto, pueden modelarse utilizando un modelo de corrección de errores vectoriales.
Además, se ha introducido el concepto de agrupamiento de volatilidad y demostrado cómo se puede emplear la función garchFit() del paquete fGarch para estimar un modelo GARCH(\(1\),\(1\)) de la heterocedasticidad condicional inherente a los rendimientos del índice bursátil Wilshire 5000.
Referencias bibliográficas
Aunque se presenta el modelo ARCH como un componente en un modelo ADL(\(1\),\(1\)), se puede usar para modelar el término de error condicional de media cero de cualquier modelo de serie temporal.↩︎