2.6 Gráficos en R
No es casualidad que las primeras publicaciones sobre S y R, como Becker y Chambers (1984) e Ihaka y Gentleman (1996), se titulan “S: Un entorno interactivo para análisis de datos y gráficos” y “R: Un lenguaje para análisis de datos y gráficos,” respectivamente. R de hecho tiene gráficos poderosos.
Aquí, se presentan brevemente los gráficos “convencionales” implementados en la base de R. R también viene con un motor gráfico nuevo e incluso más flexible, llamado grid (Murrell 2005), que proporciona la base para una implementación de gráficos en R del tipo “trellis” (Cleveland 1993) en el paquete lattice (Sarkar 2002), pero estos están más allá del alcance de este curso. Una excelente descripción de los gráficos en R se da en Murrell(2005).
La función plot()
La función básica es el método predeterminado plot(). Es una función genérica y tiene métodos para muchos objetos, incluidos marcos de datos, series de tiempo y modelos lineales ajustados. A continuación, se describe el valor predeterminado del método plot(), que puede crear varios tipos de diagramas de dispersión, pero muchas otras explicaciones se extienden a diversos métodos, así como a otras funciones de trazado de alto nivel.
El diagrama de dispersión (scatterplot) es probablemente la representación gráfica más común en estadística. Un diagrama de dispersión de Y vs. X está disponible haciendo uso de la función plot(x, y). A modo de ilustración, se vuelve a utilizar el conjunto de datos Journals del paquete AER, tomado de Stock y Watson (2007). Como se señaló antes, los datos brindan alguna información sobre las suscripciones a revistas de economía en bibliotecas estadounidenses para el año 2000. El archivo contiene \(180\) observaciones (las revistas) sobre \(10\) variables, entre ellas el número de suscripciones a bibliotecas (subs), el precio de suscripción a la biblioteca (price), y el número total de citas de la revista (citations).
Aquí, interesa la relación entre el número de suscripciones y el precio por cita. El siguiente fragmento de código deriva la variable requerida citeprice y grafica el número de suscripciones a la biblioteca en logaritmos:
# cargar los datos
data("Journals", package = "AER")
# crear la variable "citeprice"
Journals$citeprice <- Journals$price/Journals$citations
# crear el gráfico
attach(Journals)
plot(log(subs), log(citeprice))
rug(log(subs))
rug(log(citeprice), side = 2)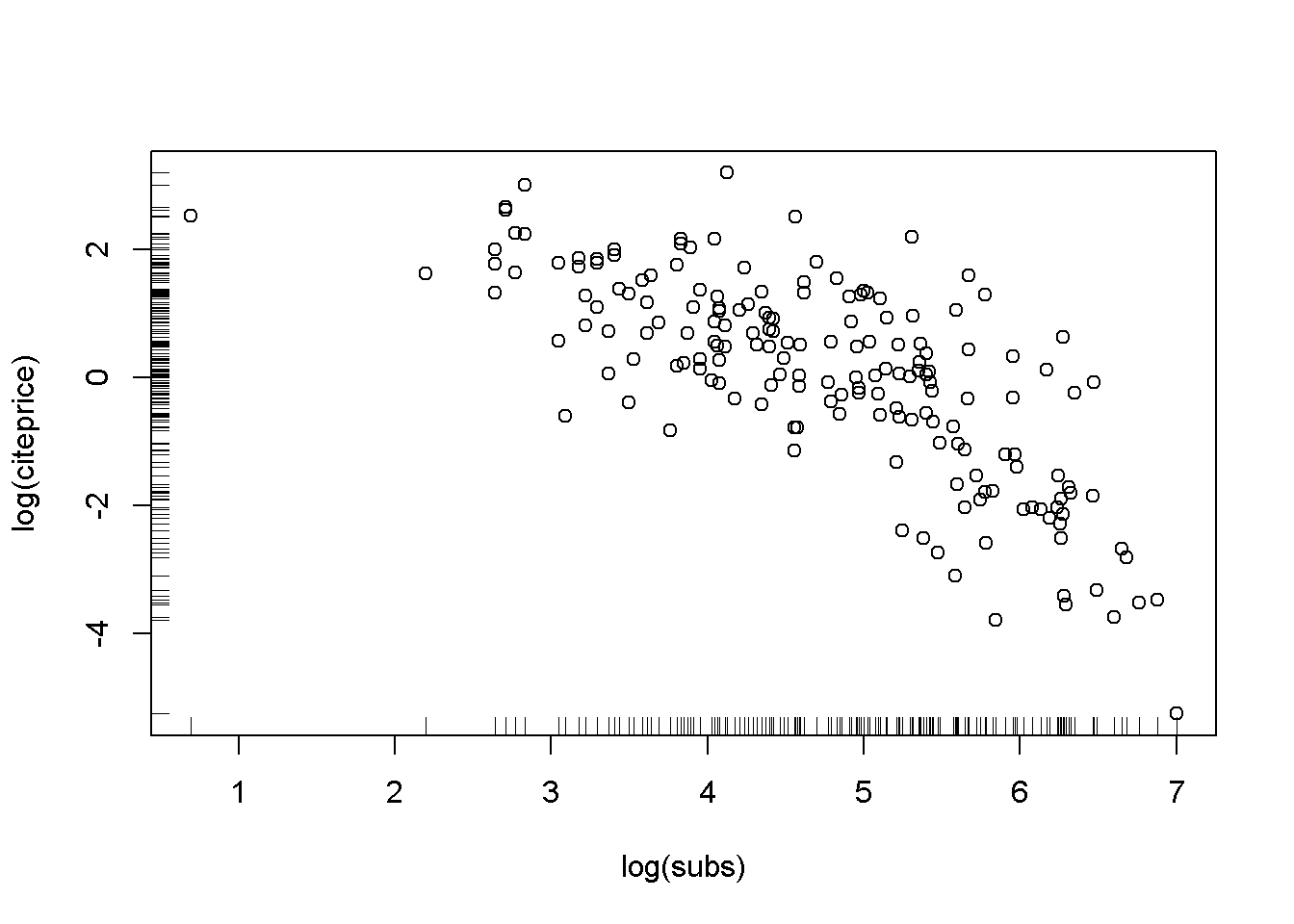
detach(Journals)La función rug() agrega pequeñas barras, visualizando así las distribuciones marginales de las variables, a lo largo de uno o ambos ejes de una gráfica existente. La gráfica resultante tiene marcas en los ejes horizontal y vertical. Una forma alternativa de especificar plot(x, y) es utilizar el método de fórmula de plot(); es decir, plot(y ~ x). Esto conduce al mismo diagrama de dispersión, pero tiene la ventaja de que se puede especificar el argumento data. Por lo tanto, se puede evitar adjuntar y desadjuntar el marco de datos:
plot(log(subs) ~ log(citeprice), data = Journals)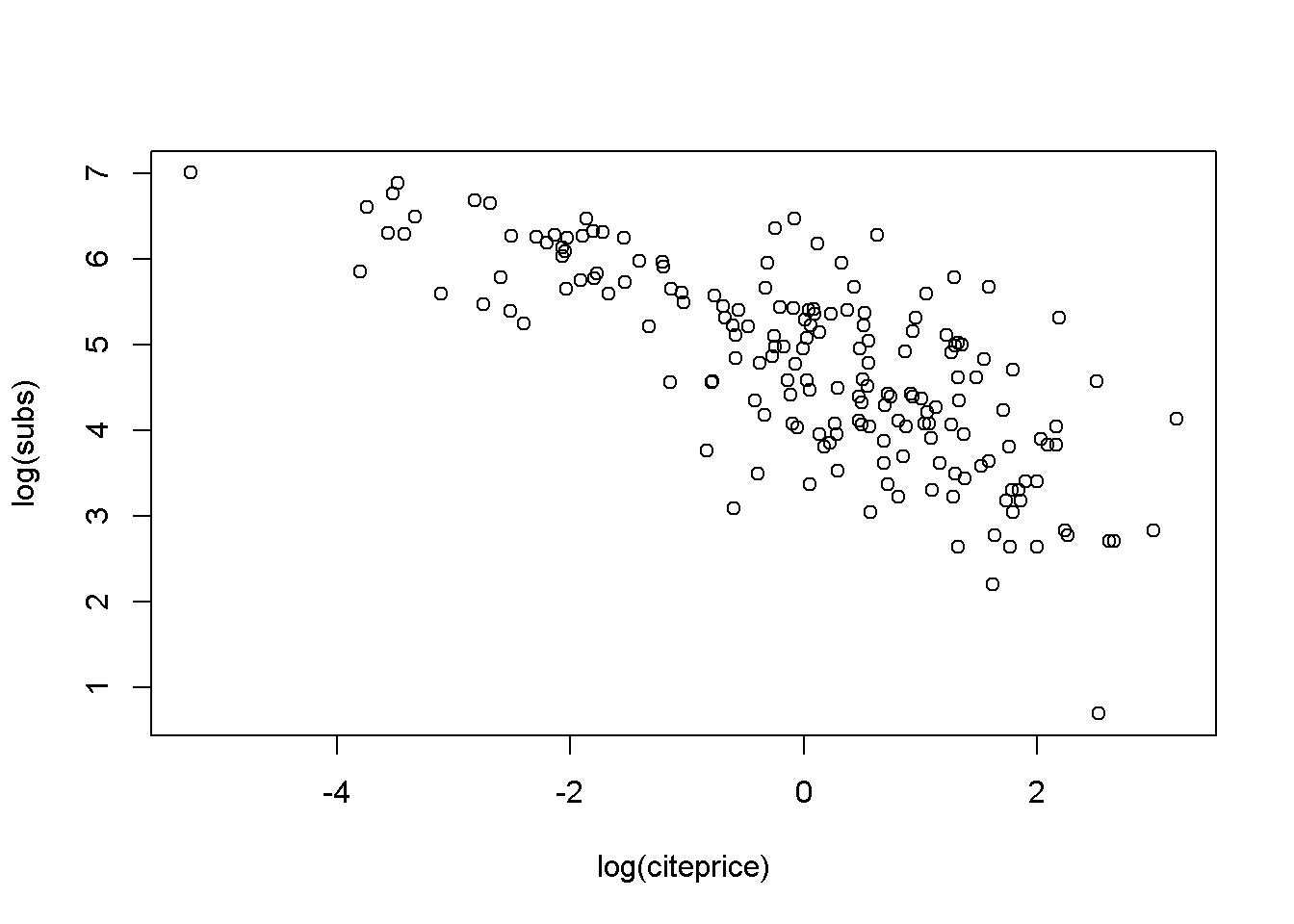
Parámetros gráficos
Todo esto parece engañosamente simple, pero el resultado puede modificarse de muchas formas. Por ejemplo, plot() toma un argumento type que controla los puntos o points (type = “p”, de manera predeterminada), las líneas o lines (type = “l”), ambas cosas o both (type = “b”) y los escalones de la escalera o steps (type = “s”), con lo que se pueden generan más tipos de gráficos. La anotación se puede modificar cambiando las etiquetas del título principal (main), el eje x (xlab) o el eje y (ylab). Se recomienda ver ?plot para más detalles.
Además, existen varias docenas de parámetros gráficos (ver ?par para ver la lista completa) que se pueden modificar configurándolos con par() o sustituyéndolos a la función plot(). Una lista selectiva de argumentos para par():
| Argumento | Descripción |
|---|---|
| axes | ¿Deberían dibujarse los ejes? |
| bg | Color de fondo |
| cex | Tamaño de un punto o símbolo |
| col | Color |
| las | Orientación de las etiquetas de los ejes |
| lty, lwd | Tipo de línea y ancho de línea |
| main, sub | Título y subtítulo |
| mar | Tamaño de los márgenes |
| mfcol, mfrow | Matriz que define el diseño para varios gráficos en un gráfico |
| pch | Símbolo de trazado |
| type | Tipos (ver texto) |
| xlab, ylab | Etiquetas de eje |
| xlim, ylim | Rangos de ejes |
| xlog, ylog, log | Escalas logarítmicas |
No se puede explicar todos estos aquí, pero se deben destacar algunos parámetros importantes:
- col establece el (los) color (es).
- ylim Y xlim ajustaN los rangos de trazado.
- Si se trazan puntos, pch puede modificar el carácter de la trama y cex la extensión del carácter.
- Si se trazan líneas, lty y lwd especifican el tipo de línea y el ancho, respectivamente.
- El tamaño de las etiquetas, marcas de eje, entre otros, se puede cambiar escribiendo el argumentos cex como cex.lab y cex.axis.
Una breve lista de argumentos para par() se proporciona en la Tabla 1.1. Esto es solo la punta del iceberg, por ende, se introducirán más parámetros gráficos a medida que se avance en el curso.
Como ejemplo simple, se puede probar:
plot(log(subs) ~ log(citeprice),
data = Journals,
pch = 20,
col = "blue",
ylim = c(0, 8),
xlim = c(-7, 4),
main = "Suscripciones a bibliotecas")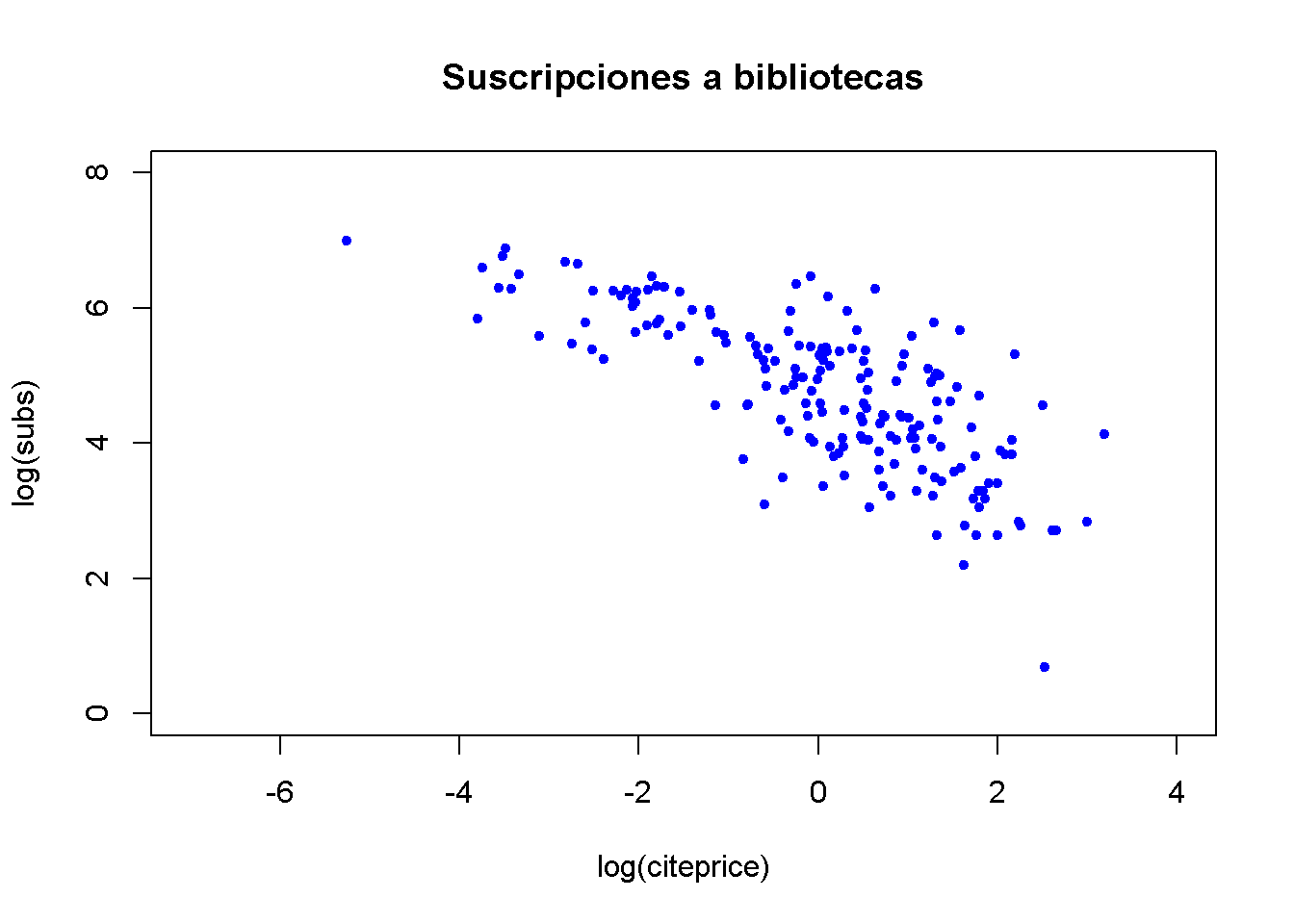
Esto produce círculos sólidos (pch = 20) en lugar de los abiertos predeterminados, dibujados en azul, y existen rangos más amplios en las direcciones de X y Y. Igualmente, se agregó un título principal.
También es posible agregar más capas a un gráfico. Por lo tanto, se pueden agregar más características con lines(), points(), text() y legend(), que aportan a una trama existente lo que sugieren sus nombres. Por ejemplo, , text(-3.798, 5.846, “Econometrica,” pos = 2), coloca una cadena de caracteres en la ubicación indicada (es decir, a la izquierda del punto). En los análisis de regresión, a menudo se desea agregar una línea de regresión a un diagrama de dispersión. Como se vio antes, esto se logra usando abline(a, b), dónde a es la intersección y b es la pendiente.
En este punto, no parece haber una gran necesidad de todo esto; sin embargo, la mayoría de los usuarios requieren un control preciso de las presentaciones visuales en algún momento, especialmente cuando se necesitan gráficos con calidad de publicación. Me abstengo de presentar ejemplos artificiales jugando con las opciones gráficas; en su lugar, se introducen variaciones de las pantallas estándar a medida que se vaya avanzando.
Por supuesto, existen muchas más funciones de trazado además del método predeterminado plot(). Por ejemplo, las visualizaciones estadísticas estándar como gráficos de barras, gráficos circulares, gráficos de caja, gráficos QQ o histogramas están disponibles en las funciones barplot(), pie(), boxplot(), qqplot() e hist(), respectivamente. Resulta instructivo correr el código demo(“graphics”) para obtener una descripción general de las impresionantes comodidades gráficas de R.
Exportación de gráficos
En el uso interactivo, los gráficos generalmente se escriben en una ventana de gráficos para que puedan inspeccionarse directamente. Sin embargo, después de completar un análisis, normalmente se quieren guardar los gráficos resultantes (por ejemplo, para su publicación en un informe, artículo de revista o tesis). Para los usuarios de Microsoft Windows y Microsoft Word, una opción simple consiste en “copiarlos y pegarlos” en el documento de Microsoft Word.
Para otros programas, como LATEX, es preferible exportar el gráfico a un archivo externo. Para ello, existen varios dispositivos gráficos en los que se puede escribir los gráficos. Los dispositivos que están disponibles en todas las plataformas incluyen los formatos vectoriales PostScript y PDF; otros dispositivos, como los formatos de mapa de bits PNG y JPEG y el formato vectorial WMF, solo están disponibles si el sistema los admite (consulte ?Devices para mas detalles).
Todos funcionan de la misma manera:
- Se abre el dispositivo; por ejemplo, la función pdf() abre el dispositivo PDF.
- Se ejecutan los comandos que crean el gráfico.
- El dispositivo se cierra mediante dev.off().
Un ejemplo simple de creación de un gráfico en un dispositivo PDF es:
pdf("mi_archivo.pdf", height = 5, width = 6)
plot(1:20, pch = 1:20, col = 1:20, cex = 2)
dev.off()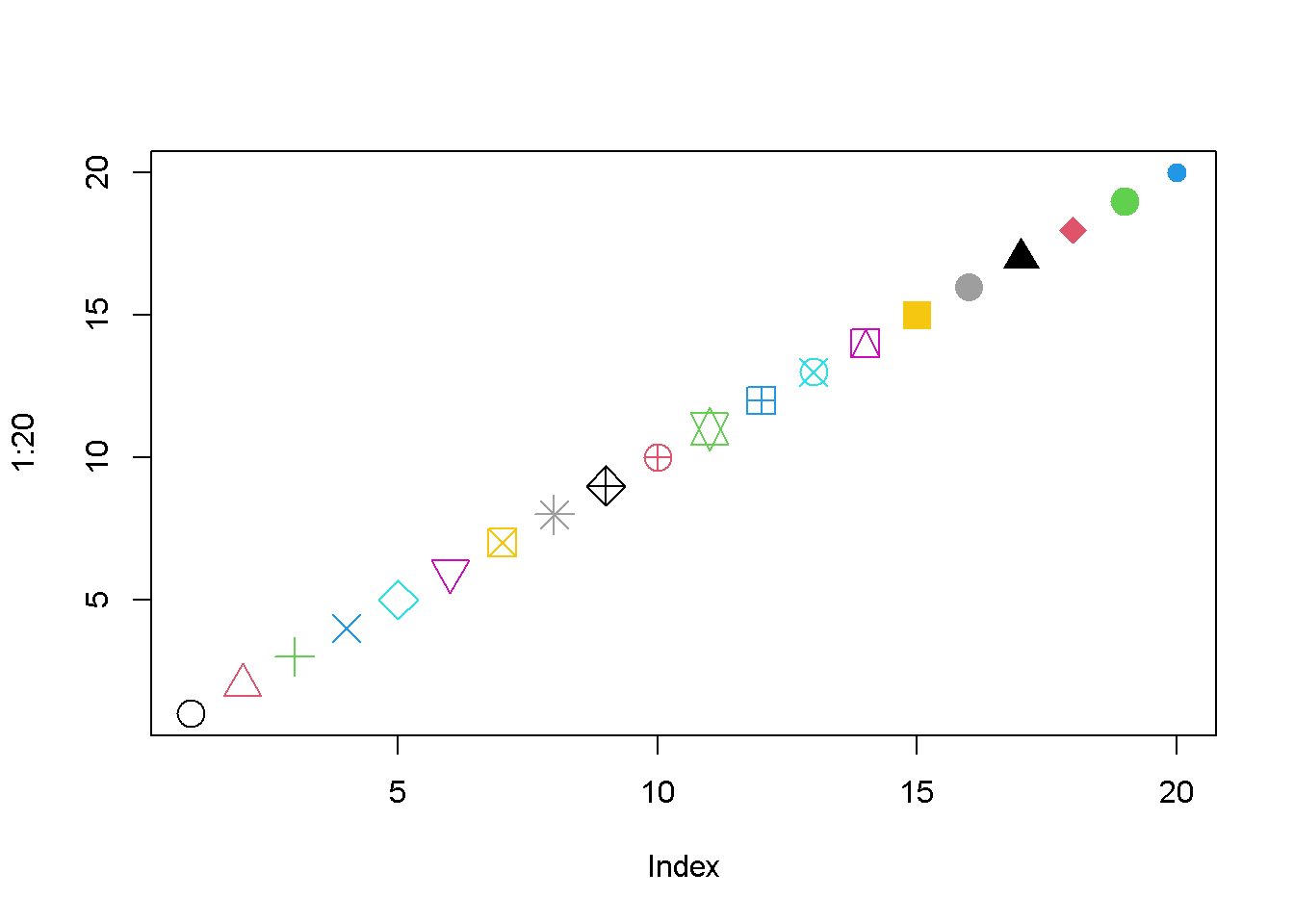
Esto crea el archivo PDF mi_archivo.pdf en el directorio de trabajo actual, que contiene el gráfico generado al llamar a la función plot(). Por cierto, el gráfico ilustra algunos de los parámetros discutidos anteriormente:
- Muestra los primeros 20 símbolos de trazado.
- Todos los símbolos de trazado se encuentran en tamaño doble.
- R enumera un conjunto de colores con los que se puede trabajar. Los primeros ocho colores son negro, rojo, verde, azul, turquesa, violeta, amarillo y gris. Desde el color nueve en adelante, este vector simplemente se recicla.
Alternativamente para abrir, imprimir y cerrar un dispositivo, también es posible imprimir un trazado existente en la ventana gráfica en un dispositivo usando dev.copy() y dev.print() (se recomienda consultar las páginas de los manuales correspondiente para obtener más información).
Anotación matemática de parcelas
Una característica que se suma particularmente a las fortalezas R cuando se trata de gráficos con calidad de publicación es su capacidad para agregar anotaciones matemáticas a los gráficos (Murrell e Ihaka 2000). Una comando S que contiene una expresión matemática puede pasar como una función de trazado sin ser evaluada; es decir, se procesa como una anotación del gráfico creado. Los lectores familiarizados con LATEX no tendrán dificultades para adaptarse a la sintaxis empleada (para obtener más detalles, consulte ?plotmath y demo(“plotmath”)). Como ejemplo, el siguiente gráfico proporciona la densidad de una distribución normal estándar (proporcionada por la funcióon dnorm() en R), incluyendo su definición matemática:
\[ f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} \]
Se obtiene a través de:
# gráfico de la densidad de la distribución normal estándar
curve(dnorm,
from = -5,
to = 5,
col = "slategray",
lwd = 3,
main = "Densidad de la distribución normal estándar")
# expresión matemática
text(-5,
0.3,
expression(f(x) == frac(1, sigma ~~sqrt(2*pi)) ~~ e^{-frac((x - mu)^2, 2*sigma^2)}),
adj = 0)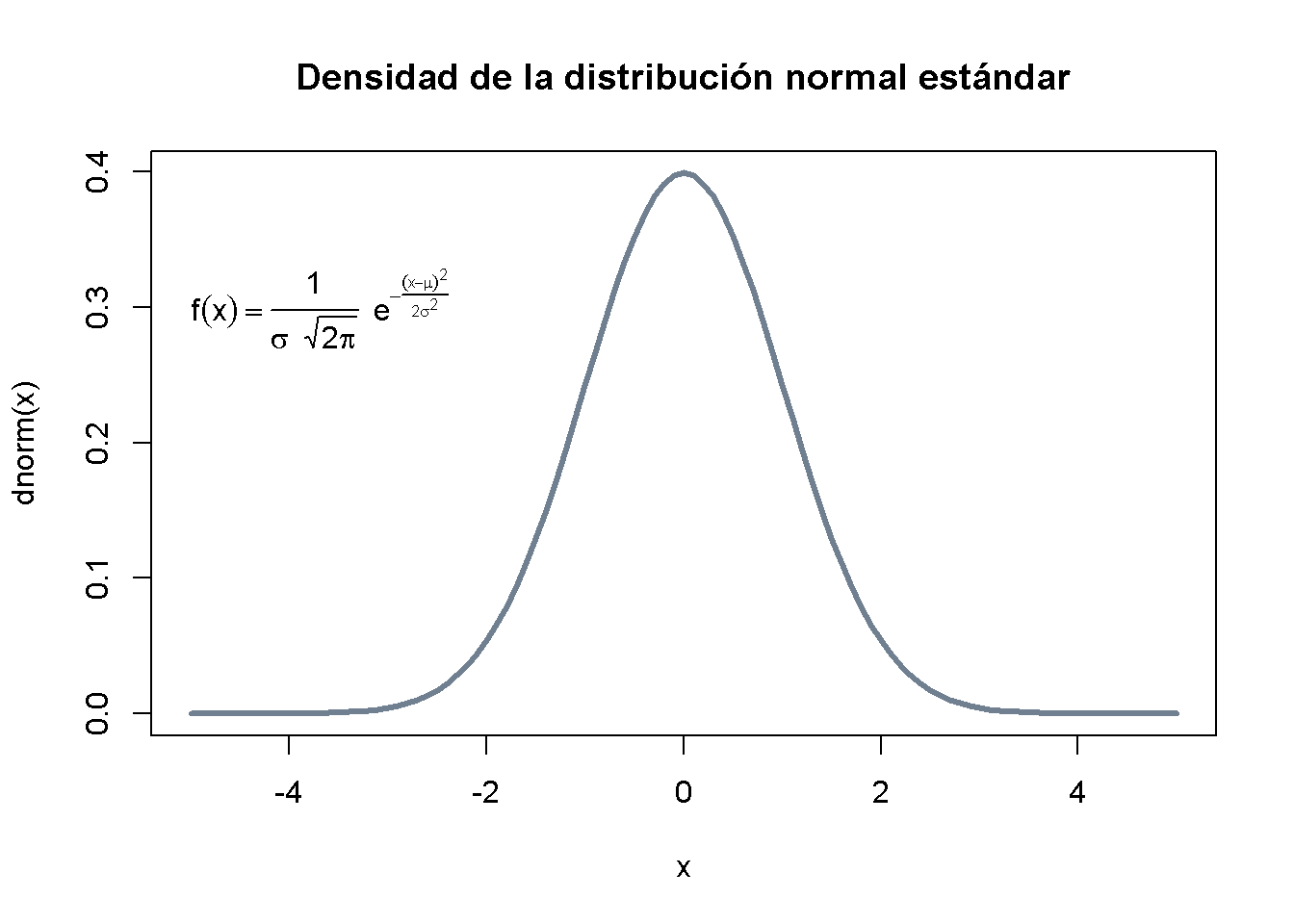
La función curve() traza la función de densidad dnorm(), mientras que la función text() se usa para agregar expression() que contiene la fórmula de la trama. Este ejemplo concluye la breve introducción a los gráficos en R.