8.5 Especificación de modelo para regresión múltiple
Elegir una especificación de regresión; es decir, seleccionar las variables que se incluirán en un modelo de regresión, es una tarea difícil. Sin embargo, existen algunas pautas sobre cómo proceder. El objetivo es claro: Obtener una estimación imparcial y precisa del efecto causal de interés.
Como punto de partida, piense en las variables omitidas; es decir, para evitar posibles sesgos mediante el uso de variables de control adecuadas. El sesgo de las variables omitidas en el contexto de la regresión múltiple se explica en el Concepto clave 7.3.
Un segundo paso podría ser comparar diferentes especificaciones por medidas de ajuste. Sin embargo, como se puede observar, uno no debería depender únicamente de \(\bar{R}^2\).
Concepto clave 7.3
Sesgo variable omitido en regresión múltiple
El sesgo de variable omitida es el sesgo en el estimador de MCO que surge cuando los regresores se correlacionan con una variable omitida. Para que surja un sesgo de variable omitida, dos cosas deben ser ciertas:
- Al menos uno de los regresores incluidos debe estar correlacionado con la variable omitida.
- La variable omitida debe ser un determinante de la variable dependiente, \(Y\).
Ahora se discute un ejemplo en el que se enfrenta un posible sesgo de variable omitida en un modelo de regresión múltiple:
Considere nuevamente la ecuación de regresión estimada:
\[ \widehat{TestScore} = \underset{(8.7)}{686.0} - \underset{(0.43)}{1.10} \times size - \underset{(0.031)}{0.650} \times english. \]
Se está interesado en estimar el efecto causal del tamaño de la clase en la puntuación de la prueba. Podría haber un sesgo debido a la omisión de “oportunidades de aprendizaje externas” en la regresión, ya que tal medida podría ser un determinante de los puntajes de las pruebas de los estudiantes y también podría correlacionarse con ambos regresores ya incluidos en el modelo (de modo que ambas condiciones de del Concepto clave 7.3 se cumplen). Las “oportunidades de aprendizaje externo” son un concepto complicado que es difícil de cuantificar. Un sustituto que se puede considerar, en cambio, es el entorno económico de los estudiantes que probablemente esté fuertemente relacionado con las oportunidades de aprendizaje externas: Piense en padres adinerados que pueden proporcionar tiempo y/o dinero para la matrícula privada de sus hijos. Por lo tanto, se aumenta el modelo con la variable lunch, el porcentaje de estudiantes que califican para un almuerzo gratis o subsidiado en la escuela debido a ingresos familiares por debajo de cierto umbral, y reestimar el modelo.
# estimar el modelo e imprimir el resumen en la consola
model <- lm(score ~ size + english + lunch, data = CASchools)
coeftest(model, vcov. = vcovHC, type = "HC1")
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 700.149957 5.568453 125.7351 < 2.2e-16 ***
#> size -0.998309 0.270080 -3.6963 0.0002480 ***
#> english -0.121573 0.032832 -3.7029 0.0002418 ***
#> lunch -0.547345 0.024107 -22.7046 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Por tanto, la recta de regresión estimada es
\[ \widehat{TestScore} = \underset{(5.56)}{700.15} - \underset{(0.27)}{1.00} \times size - \underset{(0.03)}{0.12} \times english - \underset{(0.02)}{0.55} \times lunch. \]
No se observan cambios sustanciales en la conclusión sobre el efecto de \(size\) en \(TestScore\): El coeficiente de \(size\) cambia solo \(0.1\) y conserva su importancia.
Aunque la diferencia en los coeficientes estimados no es grande, en este caso, es útil mantener lunch para hacer más creíble el supuesto de independencia media condicional.
Especificación del modelo en teoría y en la práctica
El Concepto clave 7.4 enumera algunos errores comunes al usar \(R^2\) y \(\bar{R}^2\) para evaluar la capacidad predictiva de los modelos de regresión.
Concepto clave 7.4
\(R^2\) y \(\bar{R}^2\): lo que te dicen — y lo que no
\(R^2\) y \(\bar{R}^2\) indican si los regresores son buenos para explicar la variación de la variable independiente en la muestra. Si \(R^2\) (o \(\bar{R}^2\)) es casi \(1\), entonces los regresores producen una buena predicción de la variable dependiente en esa muestra, en el sentido de que la varianza de los residuales de MCO es pequeña en comparación con la varianza de la variable dependiente. Si \(R^2\) (o \(\bar{R}^2\)) es casi \(0\), lo contrario es cierto.
La \(R^2\) y \(\bar{R}^2\) no indican si:
- Una variable incluida es estadísticamente significativa.
- Los regresores son la verdadera causa de los movimientos en la variable dependiente (causalidad).
- Existe sesgo de variable omitida.
- Se ha elegido el conjunto de regresores más apropiado.
Por ejemplo, piense en hacer una regresión de \(TestScore\) en \(PLS\), que mide el espacio de estacionamiento disponible en miles de pies cuadrados. Es probable que observe un coeficiente significativo de magnitud razonable y valores de moderados a altos para \(R^2\) y \(\bar{R}^2\). La razón de esto es que el espacio en el estacionamiento se correlaciona con muchos factores determinantes de la puntuación de la prueba, como la ubicación, el tamaño de la clase, la dotación financiera, entre otrs. Aunque no se tienen observaciones sobre \(PLS\), se puede usar R para generar algunos datos relativamente realistas.
# sembrar la semilla para la reproducibilidad
set.seed(1)
# generar observaciones para el espacio de estacionamiento
CASchools$PLS <- c(22 * CASchools$income
- 15 * CASchools$size
+ 0.2 * CASchools$expenditure
+ rnorm(nrow(CASchools), sd = 80) + 3000)# geficar el espacio del estacionamiento contra el puntaje de la prueba
plot(CASchools$PLS,
CASchools$score,
xlab = "Espacio de estacionamiento",
ylab = "Resultado de la prueba",
pch = 20,
col = "steelblue")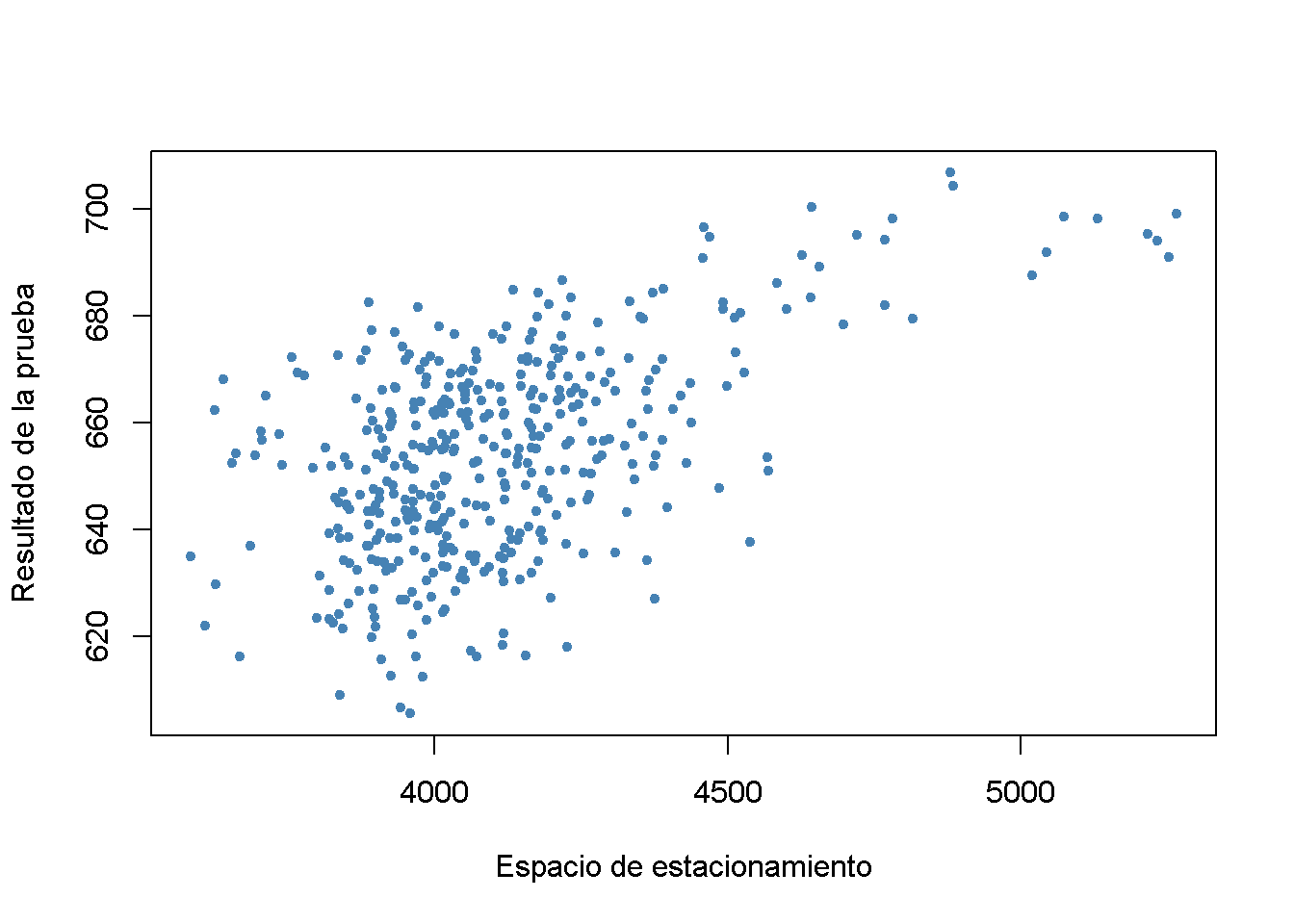
# puntuación de la prueba de regresión en PLS
summary(lm(score ~ PLS, data = CASchools))
#>
#> Call:
#> lm(formula = score ~ PLS, data = CASchools)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -42.608 -11.049 0.342 12.558 37.105
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.897e+02 1.227e+01 39.90 <2e-16 ***
#> PLS 4.002e-02 2.981e-03 13.43 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 15.95 on 418 degrees of freedom
#> Multiple R-squared: 0.3013, Adjusted R-squared: 0.2996
#> F-statistic: 180.2 on 1 and 418 DF, p-value: < 2.2e-16\(PLS\) se genera como una función lineal de \(expenditure\), \(income\), \(size\) y una perturbación aleatoria. Por lo tanto, los datos sugieren que existe una relación positiva entre el espacio de estacionamiento y la puntuación de la prueba. De hecho, al estimar el modelo
\[\begin{align} TestScore = \beta_0 + \beta_1 \times PLS + u \tag{8.1} \end{align}\]
usando lm() se encuentra que el coeficiente en \(PLS\) es positivo y significativamente diferente de cero. Además, \(R^2\) y \(\bar{R}^2\) son aproximadamente \(0.3\), que es mucho más que los aproximadamente \(0.05\) observados al hacer una regresión de los puntajes de las pruebas solo en el tamaño de las clases. Esto sugiere que aumentar el espacio de estacionamiento aumenta las calificaciones de las pruebas de la escuela y que el modelo (8.1) explica mejor la heterogeneidad en la variable dependiente que un modelo con \(size\) como único regresor. Teniendo en cuenta cómo se construye \(PLS\), esto no es ninguna sorpresa. Es evidente que el alto \(R^2\)