7.5 La distribución de los estimadores de MCO en regresión múltiple

Como en la regresión lineal simple, diferentes muestras producirán diferentes valores de los estimadores de MCO en el modelo de regresión múltiple. Una vez más, esta variación conduce a la incertidumbre de los estimadores que se busca describir utilizando su(s) distribución(es) muestral(es). En resumen, si se cumple la suposición hecha en el Concepto clave 6.4, la distribución muestral grande de \(\hat\beta_0,\hat\beta_1,\dots,\hat\beta_k\) es multivariante normal, de modo que los estimadores individuales también se distribuyen normalmente. El Concepto clave 6.5 resume las declaraciones correspondientes.

Concepto clave 6.5

Distribución de muestra grande de \(\hat\beta_0,\hat\beta_1,\dots,\hat\beta_k\)

Si se cumplen los supuestos de mínimos cuadrados en el modelo de regresión múltiple (ver Concepto clave 6.4), entonces, en muestras grandes, los estimadores de MCO \(\hat\beta_0,\hat\beta_1,\dots,\hat\beta_k\) se distribuyen normalmente de forma conjunta. También se dice que su distribución conjunta es multivariante normal. Además, cada \(\hat\beta_j\) se distribuye como \(\mathcal{N}(\beta_j,\sigma_{\beta_j}^2)\).

Esencialmente, el Concepto clave 6.5 establece que, si el tamaño de la muestra es grande, se pueden aproximar las distribuciones muestrales individuales de los estimadores de coeficientes mediante distribuciones normales específicas y su distribución muestral conjunta mediante una distribución normal multivariante.

¿Cómo se puede usar R para tener una idea de cómo se ve la FDP conjunta de los estimadores de coeficientes en el modelo de regresión múltiple? Al estimar un modelo sobre algunos datos, se termina con un conjunto de estimaciones puntuales que no revelan mucha información sobre la densidad conjunta de los estimadores. Sin embargo, con una gran cantidad de estimaciones que utilizan datos muestreados aleatoriamente repetidamente de la misma población, se puede generar un gran conjunto de estimaciones puntuales que permiten trazar una estimación de la función de densidad conjunta.

El enfoque que se usará para hacer esto en R es el siguiente:

Generar \(10000\) muestras aleatorias de tamaño \(50\) usando el DGP \[ Y_i = 5 + 2.5 \cdot X_{1i} + 3 \cdot X_{2i} + u_i \] donde los regresores \(X_{1i}\) y \(X_{2i}\) se muestrean para cada observación como \[ X_i = (X_{1i}, X_{2i}) \sim \mathcal{N} \left[\begin{pmatrix} 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 10 & 2.5 \\ 2.5 & 10 \end{pmatrix} \right] \] y \[ u_i \sim \mathcal{N}(0,5) \] es el término de error.
Para cada uno de los conjuntos de datos de muestra simulados de \(10000\), se estima el modelo \[ Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + u_i \] y se guardan las estimaciones de coeficientes \(\hat\beta_1\) y \(\hat\beta_2\).
Se calcula una estimación de densidad de la distribución conjunta de \(\hat\beta_1\) y \(\hat\beta_2\) en el modelo anterior usando la función kde2d() del paquete MASS, ver ?MASS. Esta estimación luego se grafica usando la función persp().

# cargar paquetes
library(MASS)
library(mvtnorm)

# establecer tamaño de muestra
n <- 50

# inicializar vector de coeficientes
coefs <- cbind("hat_beta_1" = numeric(10000), "hat_beta_2" = numeric(10000))

# sembrar la semilla para la reproducibilidad
set.seed(1)

# muestreo y estimación de bucles
for (i in 1:10000) {
  
  X <- rmvnorm(n, c(50, 100), sigma = cbind(c(10, 2.5), c(2.5, 10)))
  u <- rnorm(n, sd = 5)
  Y <- 5 + 2.5 * X[, 1] + 3 * X[, 2] + u
  coefs[i,] <- lm(Y ~ X[, 1] + X[, 2])$coefficients[-1]
  
}

# calcular la estimación de la densidad
kde <- kde2d(coefs[, 1], coefs[, 2])

# graficar densidad de estimación
persp(kde, 
      theta = 310, 
      phi = 30, 
      xlab = "beta_1", 
      ylab = "beta_2", 
      zlab = "Densidad de estimación")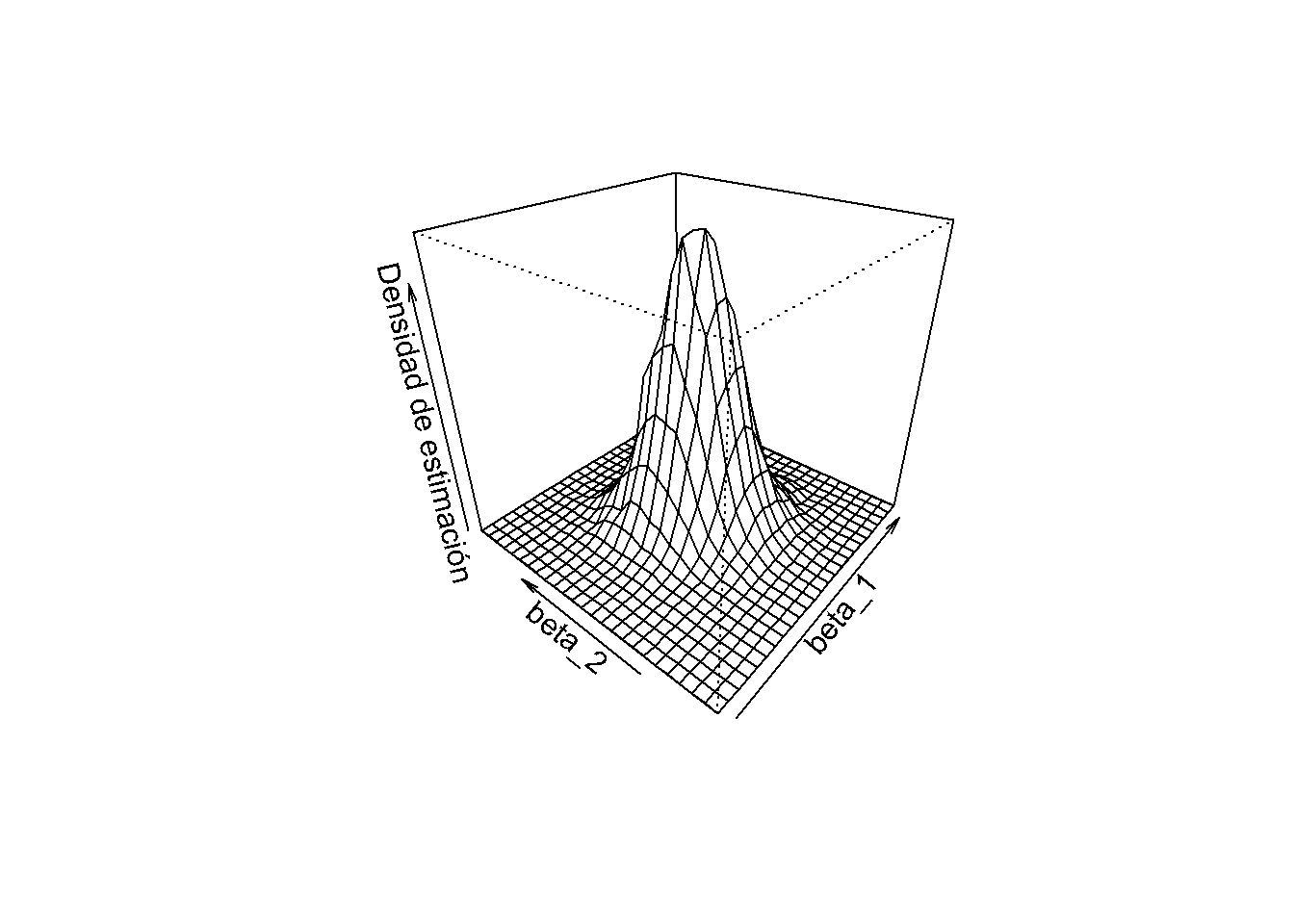

En el gráfico anterior, se puede ver que la estimación de densidad tiene cierta similitud con una distribución normal bivariada (consulte el Capítulo 3), aunque no es muy bonita y probablemente un poco aproximada. Además, existe una correlación entre las estimaciones tal que \(\rho\neq0\) (2.1). Además, la forma de la distribución se desvía de la forma de campana simétrica de la distribución normal estándar bivariada y, en cambio, tiene un área de superficie elíptica.

# estimar la correlación entre estimadores
cor(coefs[, 1], coefs[, 2])
#> [1] -0.2503028

¿De dónde proviene esta correlación? Observe que, debido a la forma en que se generan los datos, existe una correlación entre los regresores \(X_1\) y \(X_2\). La correlación entre los regresores en un modelo de regresión múltiple siempre se traduce en una correlación entre los estimadores. En este caso, la correlación positiva entre \(X_1\) y \(X_2\) se traduce en una correlación negativa entre \(\hat\beta_1\) y \(\hat\beta_2\). Para tener una mejor idea de la distribución, puede variar el punto de vista en el subsecuente suave gráfico 3D interactivo de la misma estimación de densidad utilizada para el trazado con persp(). Aquí se puede ver que la forma de la distribución está algo estirada debido a \(\rho=-0.20\) y también es evidente que ambos estimadores son insesgados ya que su densidad conjunta parece estar centrada cerca del vector de parámetro verdadero \((\beta_1,\beta_2) = (2.5,3)\).