11.2 Datos de panel con dos períodos de tiempo: Comparaciones “antes y después”

Suponga que solo existen $T = 2$ períodos de tiempo $t = 1982, 1988$. Esto permite analizar las diferencias en los cambios de la tasa de letalidad del año 1982 a 1988. Para empezar se debe considerar el modelo de regresión poblacional \[\text{Tasa de mortalidad}_{it} = \beta_0 + \beta_1 \text{Impuesto a la cerveza}_{it} + \beta_2 Z_{i} + u_{it}\] donde $Z_i$ son características específicas del estado que difieren entre los estados pero que son constantes en el tiempo. Para $t = 1982$ y $t = 1988$ se tiene:

\[\begin{align*} \text{Tasa de mortalidad}_{i1982} =&\, \beta_0 + \beta_1 \text{Impuesto a la cerveza}_{i1982} + \beta_2 Z_i + u_{i1982}, \\ \text{Tasa de mortalidad}_{i1988} =&\, \beta_0 + \beta_1 \text{Impuesto a la cerveza}_{i1988} + \beta_2 Z_i + u_{i1988}. \end{align*}\]

Se puede eliminar el $Z_i$ haciendo una regresión de la diferencia en la tasa de mortalidad entre 1988 y 1982 sobre la diferencia en el impuesto a la cerveza entre esos años:

\[\text{Tasa de mortalidad}_{i1988} - \text{Tasa de mortalidad}_{i1982} = \\\\ \beta_1 (\text{Impuesto a la cerveza}_{i1988} - \text{Impuesto a la cerveza}_{i1982}) + u_{i1988} - u_{i1982}\]

Este modelo de regresión arroja una estimación robusta de $\beta_1$, un posible sesgo debido a la omisión de $Z_i$, ya que estas influencias se eliminan del modelo. A continuación, se usa R para estimar una regresión basada en los datos diferenciados y se grafica la función de regresión estimada.

# calcular las diferencias
diff_fatal_rate <- Fatalities1988$fatal_rate - Fatalities1982$fatal_rate
diff_beertax <- Fatalities1988$beertax - Fatalities1982$beertax

# estimar una regresión usando datos diferenciados
fatal_diff_mod <- lm(diff_fatal_rate ~ diff_beertax)

coeftest(fatal_diff_mod, vcov = vcovHC, type = "HC1")
#> 
#> t test of coefficients:
#> 
#>               Estimate Std. Error t value Pr(>|t|)   
#> (Intercept)  -0.072037   0.065355 -1.1022 0.276091   
#> diff_beertax -1.040973   0.355006 -2.9323 0.005229 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La inclusión de la intersección permite un cambio en la tasa de mortalidad media en el período comprendido entre 1982 y 1988 en ausencia de un cambio en el impuesto a la cerveza.

Se obtiene la función de regresión estimada de MCO \[\widehat{\text{Tasa de mortalidad}_{i1988} - \text{Tasa de mortalidad}_{i1982}} = \\\\ - \underset{(0.065)}{0.072} - \underset{(0.36)}{1.04} \times (\text{Impuesto a la cerveza}_{i1988} - \text{Impuesto a la cerveza}_{i1982}).\]

# graficar los datos diferenciados
plot(x = diff_beertax, 
     y = diff_fatal_rate, 
     xlab = "Cambio en el impuesto a la cerveza (en dólares de 1988)",
     ylab = "Cambio en la tasa de mortalidad (muertes por 10000)",
     main = "Cambios en las tasas de mortalidad por accidentes de tráfico y los impuestos a la cerveza en 1982-1988",
     xlim = c(-0.6, 0.6),
     ylim = c(-1.5, 1),
     pch = 20, 
     col = "steelblue")

# agregar la línea de regresión para graficar
abline(fatal_diff_mod, lwd = 1.5)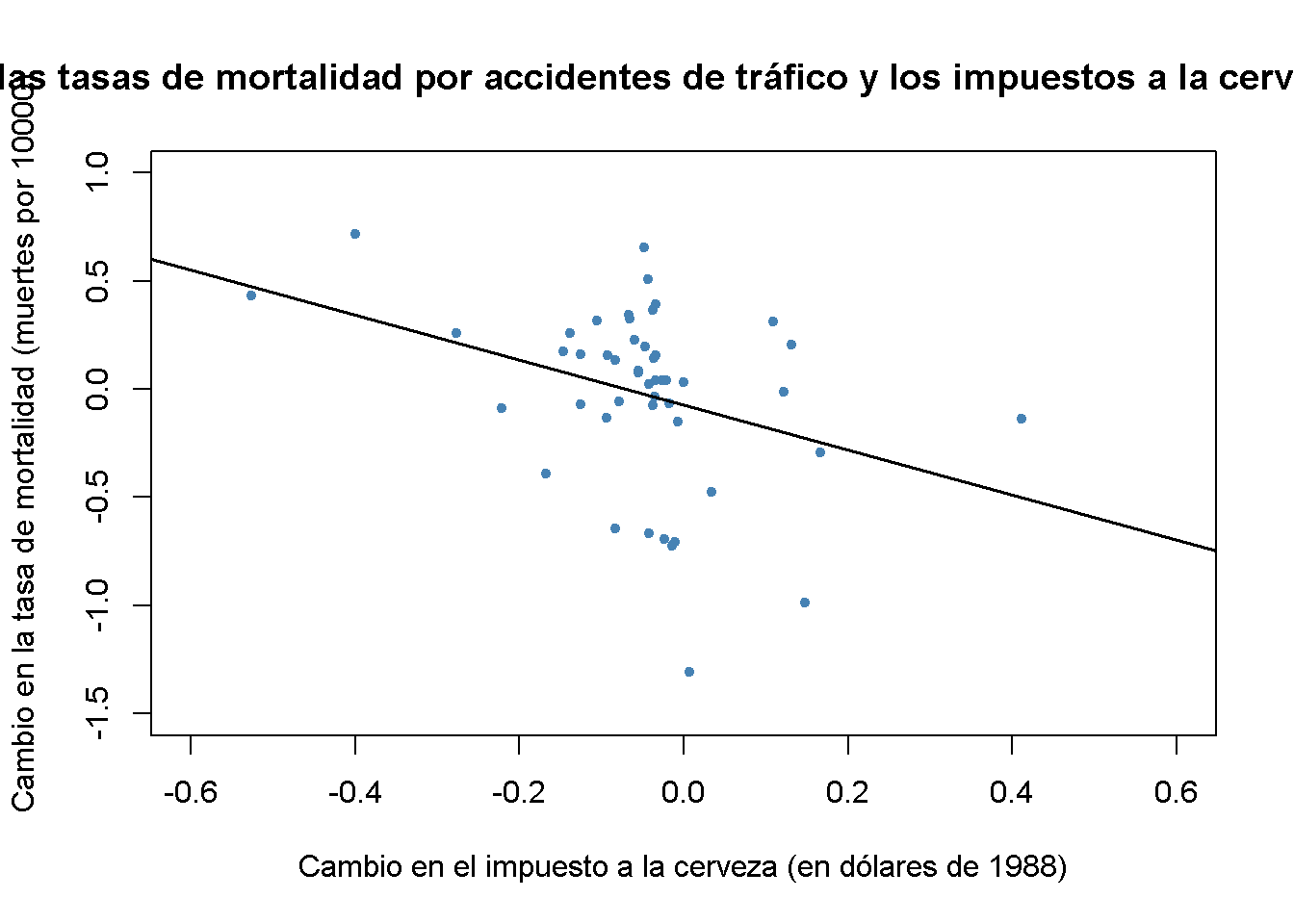

El coeficiente estimado del impuesto a la cerveza es ahora negativo y significativamente diferente de cero a $5\%$. Su interpretación es que aumentar el impuesto a la cerveza en $\$1$ hace que las muertes por accidentes de tránsito disminuyan en $1.04$ por $10000$ personas. Esto es bastante grande ya que la tasa de mortalidad promedio es de aproximadamente $2$ personas por $10000$ personas.

# calcular la tasa de mortalidad media en todos los estados para todos los períodos de tiempo
mean(Fatalities$fatal_rate)
#> [1] 2.040444

Una vez más, es probable que este resultado sea una consecuencia de la omisión de factores en la regresión de un año que influyen en la tasa de mortalidad y están correlacionados con el impuesto a la cerveza y cambian a lo largo del tiempo. El mensaje es que se debe ser más cuidadoso y controlar esos factores antes de sacar conclusiones sobre el efecto de un aumento en los impuestos a la cerveza.

El enfoque presentado en esta sección descarta información para los años $1983$ a $1987$. Un método que permite usar datos de más de $T = 2$ períodos de tiempo y permite agregar variables de control es el enfoque de regresión de efectos fijos.