6.2 Intervalos de confianza para coeficientes de regresión

Como ya se sabe, las estimaciones de los coeficientes de regresión $\beta_0$ y $\beta_1$ están sujetas a incertidumbre de muestreo, consultar el Capítulo 5. Por lo tanto, nunca se estimará exactamente el valor real de dichos parámetros a partir de datos de muestra en una aplicación empírica. Sin embargo, se pueden construir intervalos de confianza para la intersección y el parámetro de pendiente.

Un intervalo de confianza de $95\%$ para $\beta_i$ tiene dos definiciones equivalentes:

El intervalo es el conjunto de valores para los que no se puede rechazar una prueba de hipótesis al nivel de $5%$ .
El intervalo tiene una probabilidad de $95\%$ de contener el valor real de $\beta_i$ . Entonces, en el $95\%$ de todas las muestras que podrían extraerse, el intervalo de confianza cubrirá el valor real de $\beta_i$ .

También se dice que el intervalo tiene un nivel de confianza de $95\%$ . La idea del intervalo de confianza se resume en el Concepto clave 5.3.

Concepto clave 5.3

Un intervalo de confianza por $\beta_i$

Imagíne que pudiera extraer todas las muestras aleatorias posibles de un tamaño determinado. El intervalo que contiene el valor verdadero $\beta_i$ en $95\%$ de todas las muestras viene dado por la expresión:

$\text{CI}_{0.95}^{\beta_i} = \left[ \hat{\beta}_i - 1.96 \times SE(\hat{\beta}_i) \, , \, \hat{\beta}_i + 1.96 \times SE(\hat{\beta}_i) \right].$

De manera equivalente, este intervalo puede verse como el conjunto de hipótesis nulas para las que una prueba de hipótesis de dos lados $5\%$ no es rechazada.

Estudio de simulación: Intervalos de confianza

Para comprender mejor los intervalos de confianza, se realiza otro estudio de simulación. Por ahora, suponga que se tiene la siguiente muestra de $n = 100$ observaciones en una sola variable $Y$ , donde

$Y_i \overset{i.i.d}{\sim} \mathcal{N}(5,25), \ i = 1, \dots, 100.$

# establecer semillas para la reproducibilidad
set.seed(4)

# generar y graficar los datos de muestra
Y <- rnorm(n = 100, 
           mean = 5, 
           sd = 5)

plot(Y, 
     pch = 19, 
     col = "steelblue")

Se supone que los datos son generados por el modelo

$Y_i = \mu + \epsilon_i$

donde $\mu$ es una constante desconocida y se sabe que $\epsilon_i \overset{i.i.d.}{\sim} \mathcal{N}(0,25)$ . En este modelo, el estimador MCO para $\mu$ viene dado por

$\hat\mu = \overline{Y} = \frac{1}{n} \sum_{i=1}^n Y_i,$

es decir, el promedio de la muestra de $Y_i$ . Además sostiene que:

$SE(\hat\mu) = \frac{\sigma_{\epsilon}}{\sqrt{n}} = \frac{5}{\sqrt{100}}$

Un intervalo de confianza de $95\%$ de muestra grande para $\mu$ viene dado por:

$\begin{equation} CI^{\mu}_{0.95} = \left[\hat\mu - 1.96 \times \frac{5}{\sqrt{100}} \ , \ \hat\mu + 1.96 \times \frac{5}{\sqrt{100}} \right]. \tag{6.1} \end{equation}$

Es bastante fácil calcular este intervalo en R a mano. El siguiente fragmento de código genera un vector con nombre que contiene los límites del intervalo:

cbind(CIlower = mean(Y) - 1.96 * 5 / 10, CIupper = mean(Y) + 1.96 * 5 / 10)
#>       CIlower  CIupper
#> [1,] 4.502625 6.462625

Sabiendo que $\mu = 5$ , se puede ver que, para los datos del ejemplo, el intervalo de confianza cubre el valor real.

A diferencia de los ejemplos del mundo real, se puede usar R para comprender mejor los intervalos de confianza muestreando datos repetidamente, estimando $\mu$ y calculando el intervalo de confianza para $\mu$ como en (6.1).

El procedimiento es el siguiente:

Inicializar los vectores lower y upper en los que se van a guardar los límites del intervalo simulado. Se quiere simular intervalos de $10000$ para que ambos vectores tengan esta longitud.
Se usa un bucle for() para muestrear observaciones de $100$ de la distribución $\mathcal{N}(5,25)$ y calcular $\hat\mu$ así como los límites del intervalo de confianza en cada iteración del bucle.
Por fin se une lower y upper en una matriz.

# sembrar semilla
set.seed(1)

# inicializar vectores de límites de intervalo superior e inferior
lower <- numeric(10000)
upper <- numeric(10000)

# muestreo / estimación / IC de bucle
for(i in 1:10000) {
  
  Y <- rnorm(100, mean = 5, sd = 5)
  lower[i] <- mean(Y) - 1.96 * 5 / 10
  upper[i] <- mean(Y) + 1.96 * 5 / 10
  
}

# unir vectores de límites de intervalo en una matriz
CIs <- cbind(lower, upper)

Según el Concepto clave 5.3, se espera que la fracción de los intervalos simulados de $10000$ guardados en la matriz IC que contienen el valor real $\mu = 5$ debe ser aproximadamente $95\%$ . Se puede verificar esto fácilmente usando operadores lógicos.

mean(CIs[, 1] <= 5 & 5 <= CIs[, 2])
#> [1] 0.9487

La simulación muestra que la fracción de intervalos que cubren $\mu = 5$ ; es decir, aquellos intervalos para los que $H_0: \mu = 5$ no se pueden rechazar, está cerca del valor teórico de $95\%$ .

Trazar un gráfico de los primeros intervalos de confianza simulados de $100$ e indicar aquellos que no cubren el valor real de $\mu$ . Hacer esto a través de líneas horizontales que representan los intervalos de confianza uno encima del otro.

# identificar intervalos que no cubren mu
# (4 intervalos de 100)
ID <- which(!(CIs[1:100, 1] <= 5 & 5 <= CIs[1:100, 2]))

# inicializar la gráfica
plot(0, 
     xlim = c(3, 7), 
     ylim = c(1, 100), 
     ylab = "Sample", 
     xlab = expression(mu), 
     main = "Intervalos de confianza")

# configurar vector de color
colors <- rep(gray(0.6), 100)
colors[ID] <- "red"

# dibuja la línea de referencia en mu = 5
abline(v = 5, lty = 2)

# agregar barras horizontales que representen los IC
for(j in 1:100) {
  
  lines(c(CIs[j, 1], CIs[j, 2]), 
        c(j, j), 
        col = colors[j], 
        lwd = 2)
  
}

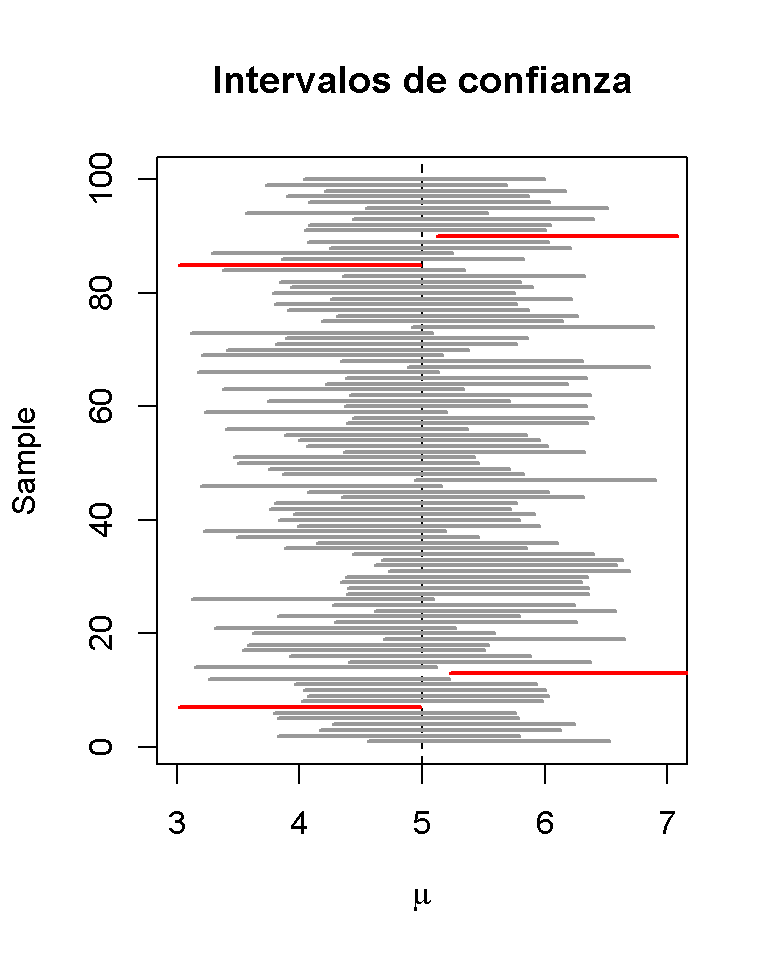
Para las primeras muestras de $100$ , la hipótesis nula verdadera se rechaza en cuatro casos, por lo que estos intervalos no cubren $\mu = 5$ . Se han indicado los intervalos que conducen a un rechazo del rojo nulo.

Volviendo al ejemplo de los resultados de las pruebas y el tamaño de las clases. El modelo de regresión del Capítulo 5 se almacena en linear_model. Una manera fácil de obtener intervalos de confianza de $95\%$ para $\beta_0$ y $\beta_1$ , los coeficientes en (intercepción) y STR, es usar la función confint(). Solo se tiene que proporcionar un objeto de modelo ajustado como entrada para esta función. El nivel de confianza está establecido en $95\%$ de forma predeterminada, pero se puede modificar configurando el argumento level, consultar ?Confint.

# calcular el intervalo de confianza del 95% para los coeficientes en 'linear_model'
confint(linear_model)
#>                 2.5 %     97.5 %
#> (Intercept) 680.32312 717.542775
#> STR          -3.22298  -1.336636

Comprobar si el cálculo se realiza como se espera para $\beta_1$ , el coeficiente de STR.

# calcular el intervalo de confianza del 95% para los coeficientes en 'linear_model' a mano
lm_summ <- summary(linear_model)

c("lower" = lm_summ$coef[2,1] - qt(0.975, df = lm_summ$df[2]) * lm_summ$coef[2, 2],
  "upper" = lm_summ$coef[2,1] + qt(0.975, df = lm_summ$df[2]) * lm_summ$coef[2, 2])
#>     lower     upper 
#> -3.222980 -1.336636

Los límites superior e inferior coinciden. Se ha utilizado el $0.975$ -cuantil de la distribución $t_{418}$ para obtener el resultado exacto informado por confint. Evidentemente, este intervalo no contiene el valor cero que, como ya se ha visto en el apartado anterior, conduce al rechazar la hipótesis nula $\beta_{1,0} = 0$ .