15.2 Datos de series de tiempo y correlación serial
El PIB se define comúnmente como el valor de los bienes y servicios producidos durante un período de tiempo determinado. El conjunto de datos us_macro_quarterly.xlsx es proporcionado por los autores y se puede descargar aquí. Proporciona datos trimestrales sobre el PIB real de Estados Unidos (es decir, ajustado por inflación) desde 1947 hasta 2004.
Como antes, un buen punto de partida es graficar los datos. El paquete quantmod proporciona algunas funciones convenientes para trazar y calcular con datos de series de tiempo. También se carga el paquete readxl para leer los datos en R.
# adjuntar el paquete 'quantmod'
library(quantmod)Se comienza importando el conjunto de datos.
# cargar datos macroeconómicos de EE. UU.
USMacroSWQ <- read_xlsx("Data/us_macro_quarterly.xlsx",
sheet = 1,
col_types = c("text", rep("numeric", 9)))
# formatear columna de fecha
USMacroSWQ$...1 <- as.yearqtr(USMacroSWQ$...1, format = "%Y:0%q")
# ajustar los nombres de las columnas
colnames(USMacroSWQ) <- c("Date", "GDPC96", "JAPAN_IP", "PCECTPI",
"GS10", "GS1", "TB3MS", "UNRATE", "EXUSUK", "CPIAUCSL")La primera columna de us_macro_quarterly.xlsx contiene texto y las restantes son numéricas. Usando col_types = c (" text “, rep (” numeric ", 9)) se indica a read_xlsx() tener esto en cuenta al importar los datos.
Es útil trabajar con objetos de series de tiempo que realizan un seguimiento de la frecuencia de los datos y son extensibles. En lo que sigue se usarán objetos de la clase xts, ver ?Xts. Dado que los datos en USMacroSWQ están en frecuencia trimestral, se convierte la primera columna al formato yearqtr antes de generar el xts objeto GDP.
# serie de PIB como objeto xts
GDP <- xts(USMacroSWQ$GDPC96, USMacroSWQ$Date)["1960::2013"]
# serie de crecimiento del PIB como objeto xts
GDPGrowth <- xts(400 * log(GDP/lag(GDP)))Los siguientes fragmentos de código reproducen un gráfico con los datos:
# gráfico (a)
plot(log(as.zoo(GDP)),
col = "steelblue",
lwd = 2,
ylab = "Logaritmo",
xlab = "Fecha",
main = "PIB real trimestral de EE. UU.")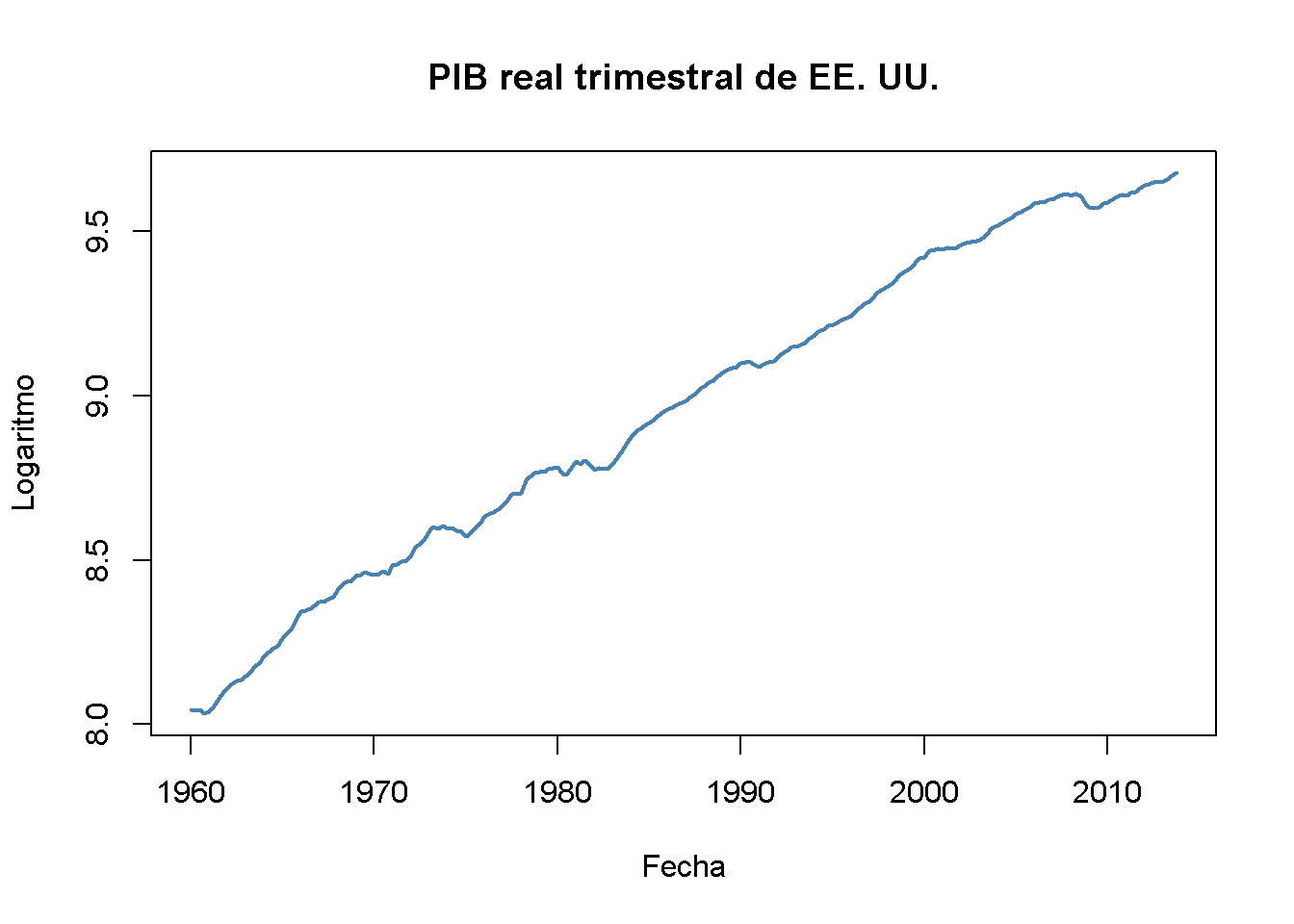
# gráfico (b)
plot(as.zoo(GDPGrowth),
col = "steelblue",
lwd = 2,
ylab = "Logaritmo",
xlab = "Fecha",
main = "Tasas de crecimiento del PIB real de EE. UU.")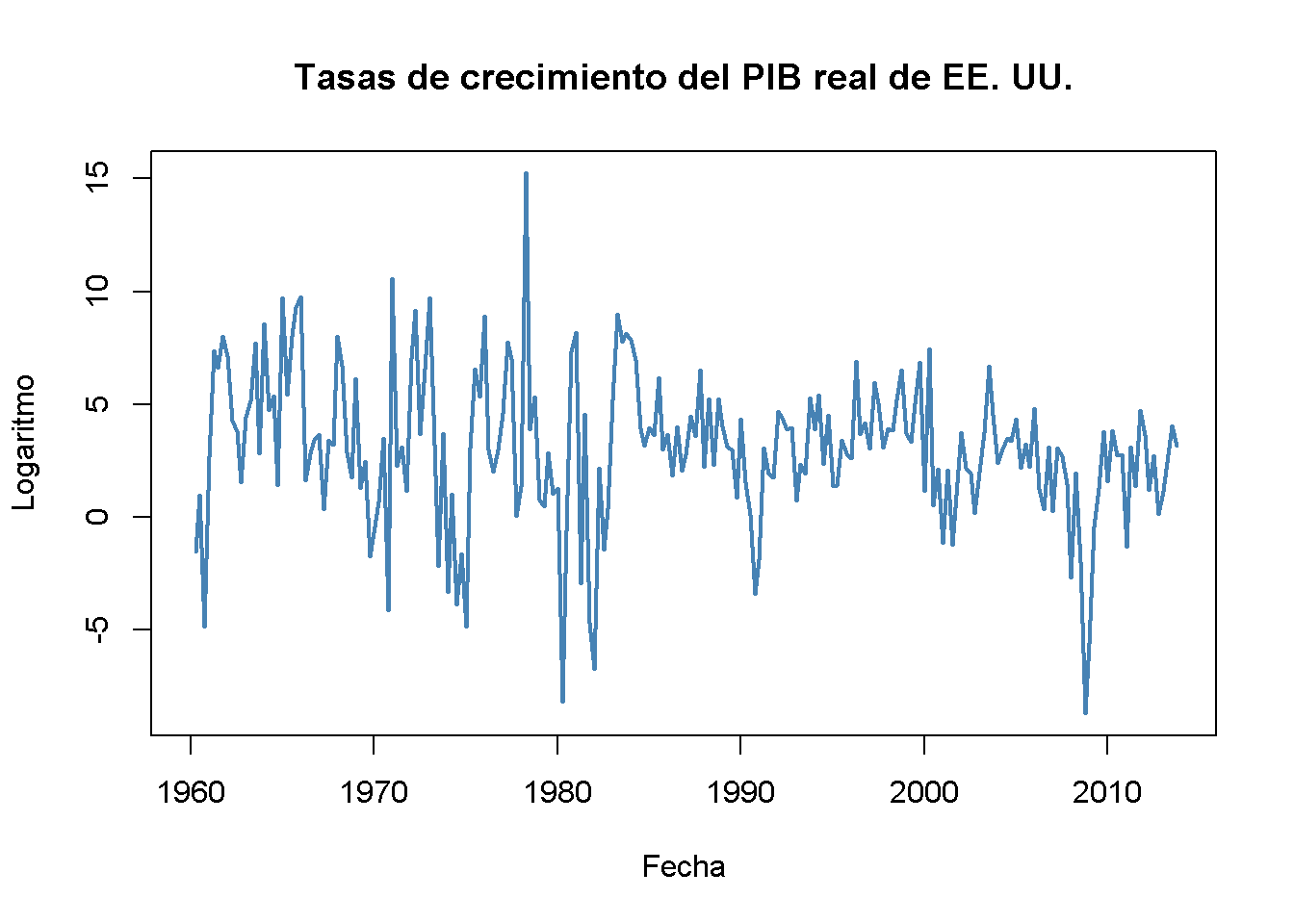
Notación, retrasos, diferencias, logaritmos y tasas de crecimiento
Para las observaciones de una variable \(Y\) registradas a lo largo del tiempo, \(Y_t\) denota el valor observado en el momento \(t\). El período entre dos observaciones secuenciales \(Y_t\) y \(Y_{t-1}\) es una unidad de tiempo: Horas, días, semanas, meses, trimestres, años, entre otros. El Concepto clave 14.1 presenta la terminología y la notación esenciales para los datos de series de tiempo que se usan en las siguientes secciones.
Concepto clave 14.1
Retrasos, primeras diferencias, logaritmos y tasas de crecimiento
Los valores anteriores de una serie de tiempo se denominan rezagos. El primer desfase de \(Y_t\) es \(Y_{t-1}\). El retraso \(j^{th}\) de \(Y_t\) es \(Y_{t-j}\). En R, los retrasos de los objetos de series de tiempo univariados o multivariados se calculan convenientemente mediante lag(), consulte ?Lag.
A veces se trabaja con series diferenciadas. La primera diferencia de una serie es \(\Delta Y_{t} = Y_t - Y_{t-1}\), la diferencia entre los períodos \(t\) y \(t-1\). Si Y es una serie de tiempo, la serie de las primeras diferencias se calcula como diff(Y).
Puede resultar conveniente trabajar con la primera diferencia en logaritmos de una serie. Se denota esto por \(\Delta \log(Y_t) = \log(Y_t) - \log(Y_{t-1})\). Para una serie de tiempo Y, esto se obtiene usando log(Y/lag(Y)).
\(100 \Delta \log (Y_t)\) es una aproximación del cambio porcentual entre \(Y_t\) y \(Y_{t-1}\).
Las definiciones hechas en el Concepto clave 14.1 son útiles debido a dos propiedades que son comunes a muchas series de tiempo económicas:
Crecimiento exponencial: Algunas series económicas crecen aproximadamente exponencialmente de tal manera que su logaritmo es aproximadamente lineal.
La desviación estándar de muchas series de tiempo económicas es aproximadamente proporcional a su nivel. Por lo tanto, la desviación estándar del logaritmo de tal serie es aproximadamente constante.
Además, es común informar las tasas de crecimiento en series macroeconómicas, por lo que a menudo se utilizan diferencias \(\log\).
A continuación se presenta la serie temporal del PIB trimestral de EE. UU; su logaritmo, la tasa de crecimiento anualizada y el primer rezago de la serie de la tasa de crecimiento anualizada para el período 2012:Q1 - 2013:Q1. La función simple serie se puede utilizar para calcular estas cantidades para una serie de tiempo trimestral.
# calcular logaritmos, tasas de crecimiento anual y el primer rezago de las tasas de crecimiento
quants <- function(series) {
s <- series
return(
data.frame("Nivel" = s,
"Logaritmo" = log(s),
"Tasa anual de crecimiento" = 400 * log(s / lag(s)),
"Primer rezago de la tasa de crecimiento anual" = lag(400 * log(s / lag(s))))
)
}La tasa de crecimiento anual se calcula usando la aproximación \[Annual Growth Y_t = 400 \cdot\Delta\log(Y_t)\], ya que \(100\cdot\Delta\log(Y_t)\) es una aproximación de los cambios porcentuales trimestrales, ver Concepto clave 14.1.
Se llama quants() a las observaciones para el período 2011:Q3 - 2013:Q1.
# obtain a data.frame with level, logarithm, annual growth rate and its 1st lag of GDP
quants(GDP["2011-07::2013-01"])
#> Nivel Logaritmo Tasa.anual.de.crecimiento
#> 2011 Q3 15062.14 9.619940 NA
#> 2011 Q4 15242.14 9.631819 4.7518062
#> 2012 Q1 15381.56 9.640925 3.6422231
#> 2012 Q2 15427.67 9.643918 1.1972004
#> 2012 Q3 15533.99 9.650785 2.7470216
#> 2012 Q4 15539.63 9.651149 0.1452808
#> 2013 Q1 15583.95 9.653997 1.1392015
#> Primer.rezago.de.la.tasa.de.crecimiento.anual
#> 2011 Q3 NA
#> 2011 Q4 NA
#> 2012 Q1 4.7518062
#> 2012 Q2 3.6422231
#> 2012 Q3 1.1972004
#> 2012 Q4 2.7470216
#> 2013 Q1 0.1452808Autocorrelación
Las observaciones de una serie temporal suelen estar correlacionadas. Este tipo de correlación se llama autocorrelación o correlación en serie. El Concepto clave 14.2 resume los conceptos de autocovarianza poblacional y autocorrelación poblacional. De igual forma, muestra cómo calcular sus equivalentes muestrales.
Concepto clave 14.2
Autocorrelación y autocovarianza
La covarianza entre \(Y_t\) y su rezago \(j^{th}\), \(Y_{t-j}\), se denomina \(j^{th}\) autocovarianza de la serie \(Y_t\). El \(j^{th}\) coeficiente de autocorrelación, también llamado coeficiente de correlación serial, mide la correlación entre \(Y_t\) y \(Y_{t-j}\). Así se tiene:
\[\begin{align*} j^{th} \text{autocovarianza} =& \, Cov(Y_t,Y_{t-j}), \\ j^{th} \text{autocorrelación} = \rho_j =& \, \rho_{Y_t,Y_{t-j}} = \frac{Cov(Y_t,Y_{t-j)}}{\sqrt{Var(Y_t)Var(Y_{t-j})}}. \end{align*}\]
La autocovarianza de la población y la autocorrelación de la población se pueden estimar mediante \(\widehat{Cov(Y_t,Y_{t-j})}\), la autocovarianza de la muestra y \(\widehat{\rho}_j\), la autocorrelación de la muestra:
\[\begin{align*} \widehat{Cov(Y_t,Y_{t-j})} =& \, \frac{1}{T} \sum_{t=j+1}^T (Y_t - \overline{Y}_{j+1:T})(Y_{t-j} - \overline{Y}_{1:T-j}), \\ \widehat{\rho}_j =& \, \frac{\widehat{Cov(Y_t,Y_{t-j})}}{\widehat{Var(Y_t)}} \end{align*}\]
\(\overline{Y}_{j+1:T}\) denota el promedio de \(Y_{j+1}, Y{j+2}, \dots, Y_T\).
En R la función acf() del paquete stats calcula la autocovarianza de muestra o la función de autocorrelación de muestra.
Usando acf() es sencillo calcular las primeras cuatro autocorrelaciones de muestra de la serie GDPGrowth.
acf(na.omit(GDPGrowth), lag.max = 4, plot = F)
#>
#> Autocorrelations of series 'na.omit(GDPGrowth)', by lag
#>
#> 0.00 0.25 0.50 0.75 1.00
#> 1.000 0.352 0.273 0.114 0.106Esto es evidencia de que existe una leve autocorrelación positiva en el crecimiento del PIB: Si el PIB crece más rápido que el promedio en un período, existe una tendencia que crece más rápido que el promedio en los siguientes períodos.
Otros ejemplos de series de tiempo económicas
Se presentan cuatro gráficos: La tasa de desempleo de EE. UU; el tipo de cambio dólar estadounidense/libra esterlina, el logaritmo del índice de producción industrial japonés, así como los cambios diarios en el índice de precios de las acciones de Wilshire 5000, una serie de tiempo financiera. El siguiente fragmento de código reproduce los gráficos de las tres series macroeconómicas y agrega cambios porcentuales en los valores diarios del índice compuesto de la Bolsa de Nueva York como cuarto (el conjunto de datos NYSESW viene con el paquete AER).
# definir series como objetos xts
USUnemp <- xts(USMacroSWQ$UNRATE, USMacroSWQ$Date)["1960::2013"]
DollarPoundFX <- xts(USMacroSWQ$EXUSUK, USMacroSWQ$Date)["1960::2013"]
JPIndProd <- xts(log(USMacroSWQ$JAPAN_IP), USMacroSWQ$Date)["1960::2013"]
# adjuntar datos de NYSESW
data("NYSESW")
NYSESW <- xts(Delt(NYSESW))# dividir el área de graficado en una matriz de 2x2
par(mfrow = c(2, 2))
# graficar la serie
plot(as.zoo(USUnemp),
col = "steelblue",
lwd = 2,
ylab = "Porcentaje",
xlab = "Fecha",
main = "Tasa de desempleo de EE. UU.",
cex.main = 1)
plot(as.zoo(DollarPoundFX),
col = "steelblue",
lwd = 2,
ylab = "Dólar por libra",
xlab = "Fecha",
main = "Tipo de cambio del dólar estadounidense / libra esterlina",
cex.main = 1)
plot(as.zoo(JPIndProd),
col = "steelblue",
lwd = 2,
ylab = "Logaritmo",
xlab = "Fecha",
main = "Producción industrial japonesa",
cex.main = 1)
plot(as.zoo(NYSESW),
col = "steelblue",
lwd = 2,
ylab = "Porcentaje por día",
xlab = "Fecha",
main = "Índice compuesto de la bolsa de valores de Nueva York",
cex.main = 1)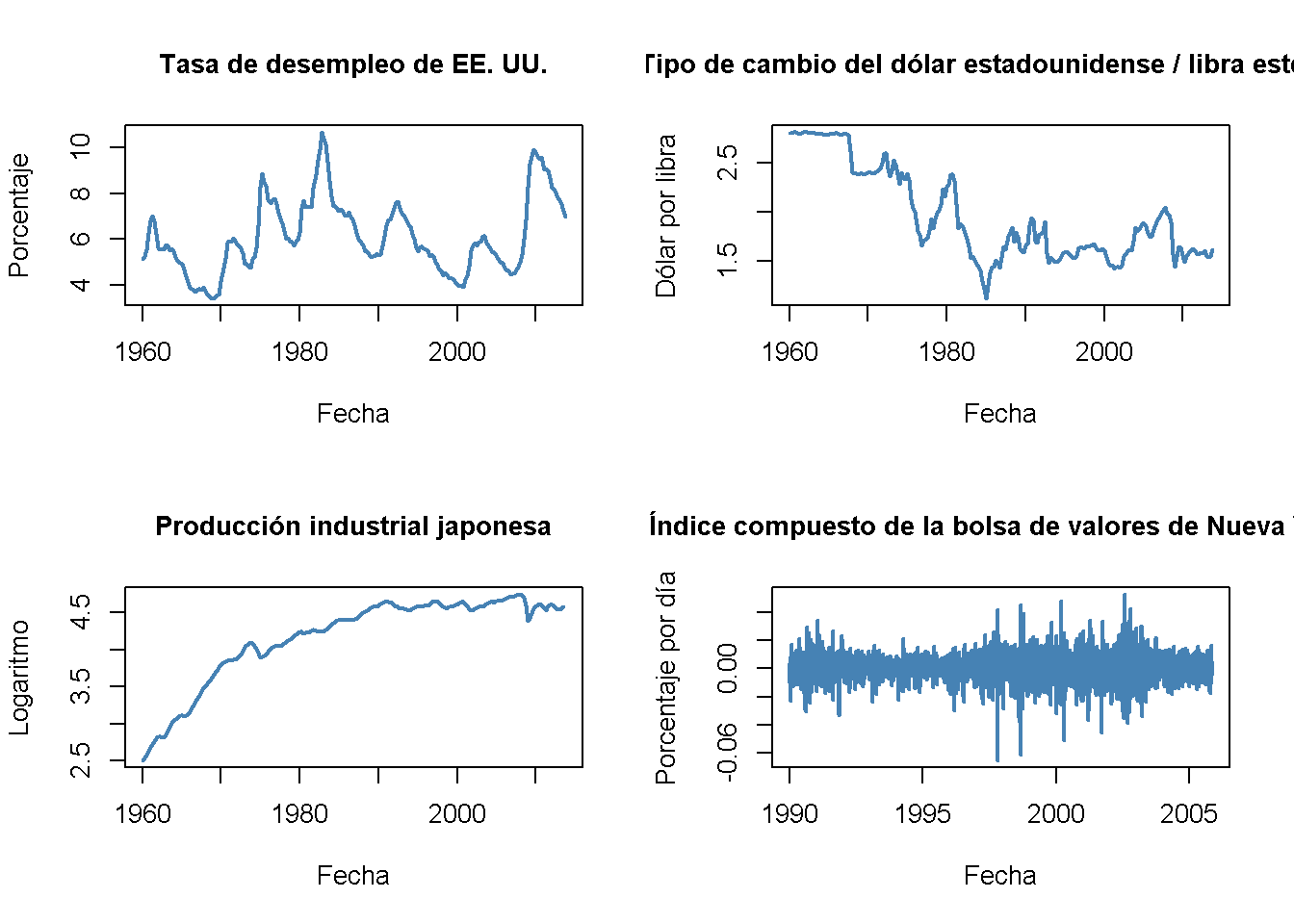
La serie presenta características bastante diferentes. La tasa de desempleo aumenta durante las recesiones y disminuye durante la recuperación económica y el crecimiento. El tipo de cambio dólar/libra muestra un patrón determinista hasta el final del sistema de Bretton Woods. La producción industrial de Japón muestra una tendencia ascendente y un crecimiento decreciente. Los cambios diarios en el índice compuesto de la Bolsa de Nueva York parecen fluctuar aleatoriamente alrededor de la línea cero. Las autocorrelaciones de muestra apoyan esta conjetura.
# calcular la autocorrelación de la muestra para la serie NYSESW
acf(na.omit(NYSESW), plot = F, lag.max = 10)
#>
#> Autocorrelations of series 'na.omit(NYSESW)', by lag
#>
#> 0 1 2 3 4 5 6 7 8 9 10
#> 1.000 0.040 -0.016 -0.023 0.000 -0.036 -0.027 -0.059 0.013 0.017 0.004Los primeros 10 coeficientes de autocorrelación de muestra están muy cerca de cero. El gráfico predeterminado generado por acf() proporciona más evidencia.
# graficar la autocorrelación de la muestra para la serie NYSESW
acf(na.omit(NYSESW), main = "Sample Autocorrelation for NYSESW Data")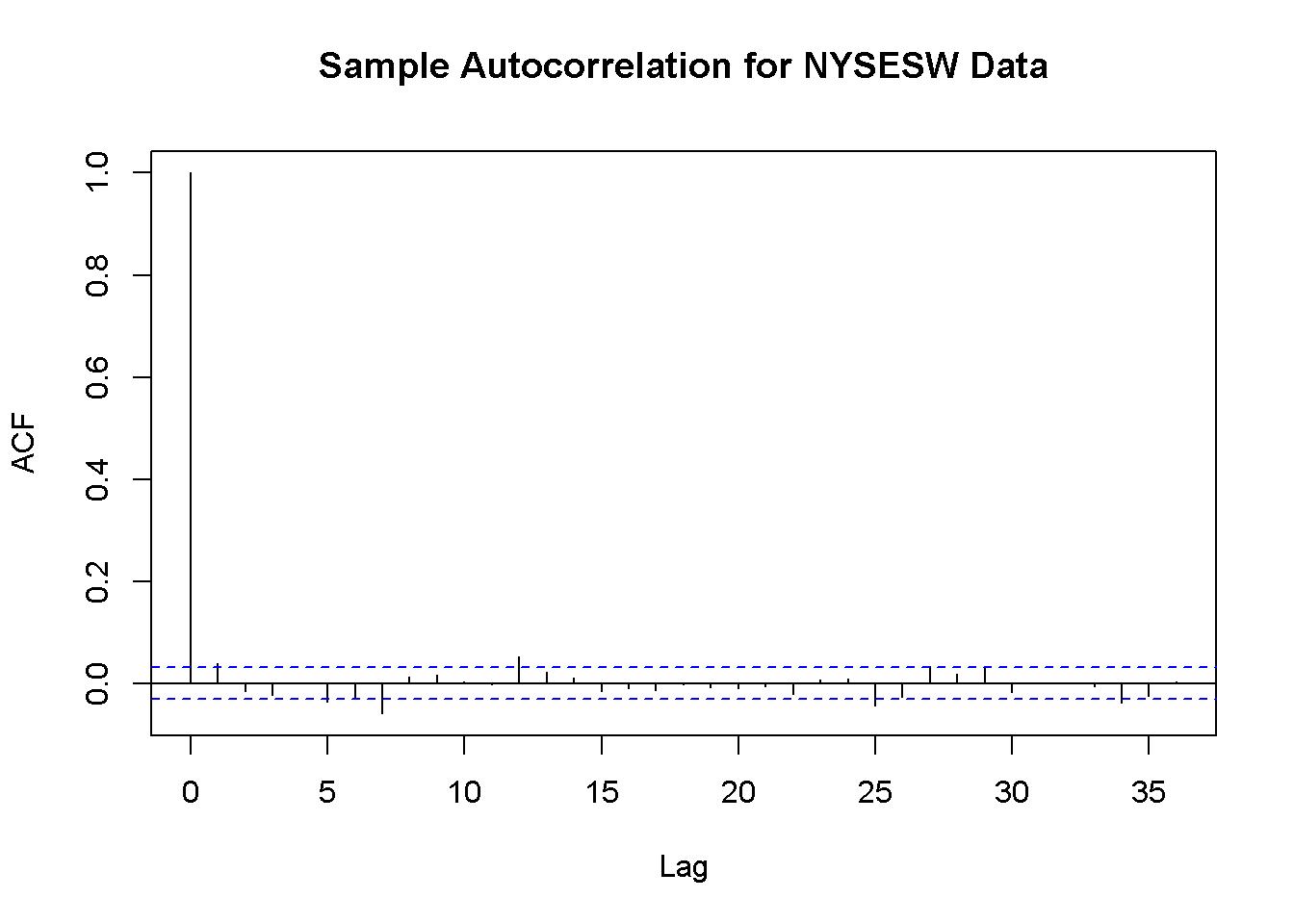
Las bandas de trazos azules representan valores más allá de los cuales las autocorrelaciones son significativamente diferentes de cero al nivel de \(5\%\). Incluso cuando las verdaderas autocorrelaciones son cero, se debe esperar algunas superaciones; recuerde la definición de error de tipo I del Concepto clave 3.5.
Para la mayoría de los rezagos, se puede ver que la autocorrelación de la muestra no excede las bandas y solo existen unos pocos casos que se encuentran marginalmente más allá de los límites.
Además, la serie NYSESW muestra lo que los econometristas llaman agrupamiento de volatilidad: Existen períodos de alta y baja variación. Esto es común para muchas series de tiempo financieras.