12.2 Regresión Probit y Logit
El modelo de probabilidad lineal tiene un defecto importante: Supone que la función de probabilidad condicional es lineal. Esto no restringe que \(P(Y=1\vert X_1,\dots,X_k)\) se encuentre entre \(0\) y \(1\). Se puede ver esto fácilmente en la reproducción de: \(P/I \ ratio \geq 1.75\), (12.2) predice que la probabilidad de que la denegación de una solicitud de hipoteca sea mayor que \(1\). Para aplicaciones con una relación \(P/I \ ratio\) cercana a \(0\), la probabilidad de negación predicha es incluso negativa, por lo que el modelo no tiene una interpretación significativa.
Esta circunstancia requiere un enfoque que utilice una función no lineal para modelar la función de probabilidad condicional de una variable dependiente binaria. Los métodos más utilizados son la regresión Probit y Logit.
Regresión Probit
En la regresión Probit, la función de distribución normal estándar acumulada \(\Phi(\cdot)\) se usa para modelar la función de regresión cuando la variable dependiente es binaria; es decir, se asume:
\[\begin{align} E(Y\vert X) = P(Y=1\vert X) = \Phi(\beta_0 + \beta_1 X). \tag{12.4} \end{align}\]
\(\beta_0 + \beta_1 X\) en (12.4) desempeña el papel de un cuantil \(z\). Recuerde que \[\Phi(z) = P(Z \leq z) \ , \ Z \sim \mathcal{N}(0,1)\], tal que el coeficiente Probit \(\beta_1\) en (12.4) es el cambio en \(z\) asociado con un cambio de una unidad en \(X\). Aunque el efecto en \(z\) de un cambio en \(X\) es lineal, el vínculo entre \(z\) y la variable dependiente \(Y\) no es lineal ya que \(\Phi\) es una función no lineal de \(X\).
Dado que la variable dependiente es una función no lineal de los regresores, el coeficiente de \(X\) no tiene una interpretación simple. De acuerdo con el Concepto clave 8.1, el cambio esperado en la probabilidad de que \(Y = 1\) debido a un cambio en \(P/I \ ratio\) se puede calcular de la siguiente manera:
- Calcular la probabilidad predicha de que \(Y = 1\) para el valor original de \(X\).
- Calcular la probabilidad predicha de que \(Y = 1\) para \(X + \Delta X\).
- Calcular la diferencia entre ambas probabilidades predichas.
Por supuesto, se puede generalizar (12.4) a la regresión Probit con regresores múltiples para mitigar el riesgo de enfrentar sesgos de variables omitidas. Los elementos esenciales de la regresión Probit se resumen en el Concepto clave 11.2.
Concepto clave 11.2
Modelo Probit, probabilidades pronosticadas y efectos estimados
Suponga que \(Y\) es una variable binaria. El modelo
\[ Y= \beta_0 + \beta_1 + X_1 + \beta_2 X_2 + \dots + \beta_k X_k + u \]
con
\[P(Y = 1 \vert X_1, X_2, \dots ,X_k) = \Phi(\beta_0 + \beta_1 + X_1 + \beta_2 X_2 + \dots + \beta_k X_k)\]
es el modelo de población Probit con múltiples regresores \(X_1, X_2, \dots, X_k\) y \(\Phi(\cdot)\) es la función de distribución normal estándar acumulativa.
La probabilidad predicha de que \(Y = 1\) dado \(X_1, X_2, \dots, X_k\) se puede calcular en dos pasos:
Calcular \(z = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k\)
Buscar \(\Phi(z)\) llamando pnorm().
\(\beta_j\) es el efecto sobre \(z\) de un cambio de una unidad en la regresión \(X_j\), manteniendo constantes todos los demás regresores \(k-1\).
El efecto sobre la probabilidad predicha de un cambio en un regresor se puede calcular como en el Concepto clave 8.1.
En R, los modelos Probit se pueden estimar usando la función glm() del paquete stats. Usando el argumento family especificando que se quiere usar una función de enlace Probit.
Ahora se estima un modelo Probit simple de la probabilidad de denegación de una hipoteca.
# estimar el modelo probit simple
denyprobit <- glm(deny ~ pirat,
family = binomial(link = "probit"),
data = HMDA)
coeftest(denyprobit, vcov. = vcovHC, type = "HC1")
#>
#> z test of coefficients:
#>
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***
#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1El modelo estimado es
\[\begin{align} \widehat{P(deny\vert P/I \ ratio}) = \Phi(-\underset{(0.19)}{2.19} + \underset{(0.54)}{2.97} P/I \ ratio). \tag{12.5} \end{align}\]
Al igual que en el modelo de probabilidad lineal, se encuentra que la relación entre la probabilidad de denegación y la relación pagos-ingresos es positiva y que el coeficiente correspondiente es altamente significativo.
El siguiente fragmento de código reproduce la Figura 11.2 del libro.
# graficar datos
plot(x = HMDA$pirat,
y = HMDA$deny,
main = "Modelo probit de probabilidad de negación, dada la relación P/I",
xlab = "Relación P/I",
ylab = "Denegar",
pch = 20,
ylim = c(-0.4, 1.4),
cex.main = 0.85)
# añadir texto y líneas discontinuas horizontales
abline(h = 1, lty = 2, col = "darkred")
abline(h = 0, lty = 2, col = "darkred")
text(2.5, 0.9, cex = 0.8, "Hipoteca denegada")
text(2.5, -0.1, cex= 0.8, "Hipoteca aprobada")
# agregar línea de regresión estimada
x <- seq(0, 3, 0.01)
y <- predict(denyprobit, list(pirat = x), type = "response")
lines(x, y, lwd = 1.5, col = "steelblue")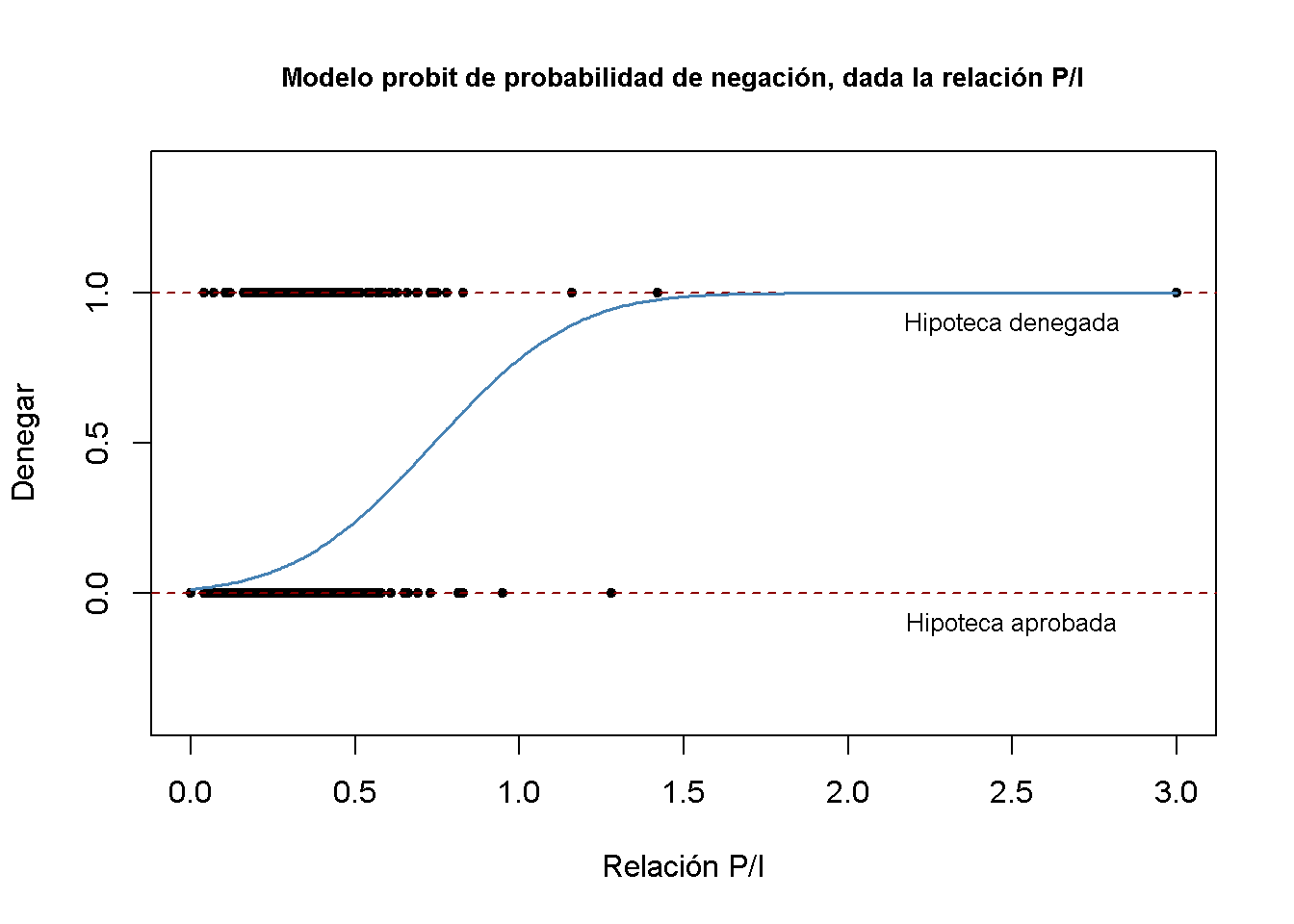
La función de regresión estimada tiene una forma de “S” estirada que es típica del FDPA de una variable aleatoria continua con FDP simétrico como el de una variable aleatoria normal. La función es claramente no lineal y se aplana para valores grandes y pequeños de \(P/I \ ratio\). Por tanto, la forma funcional también asegura que las probabilidades condicionales predichas de una negación se encuentren entre \(0\) y \(1\).
Usar predict() para calcular el cambio predicho en la probabilidad de negación cuando \(P/I \ ratio\) aumenta de \(0.3\) a \(0.4\).
# 1. calcular predicciones para la relación P/I = 0.3, 0.4
predictions <- predict(denyprobit,
newdata = data.frame("pirat" = c(0.3, 0.4)),
type = "response")
# 2. Calcular la diferencia de probabilidades
diff(predictions)
#> 2
#> 0.06081433Se predice que un aumento en la relación pago-ingreso de \(0.3\) a \(0.4\) aumentará la probabilidad de negación en aproximadamente \(6.2\%\).
Continuando utilizando un modelo Probit aumentado para estimar el efecto de la raza en la probabilidad de que se rechace una solicitud de hipoteca.
denyprobit2 <- glm(deny ~ pirat + black,
family = binomial(link = "probit"),
data = HMDA)
coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")
#>
#> z test of coefficients:
#>
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***
#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***
#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La ecuación del modelo estimado es
\[\begin{align} \widehat{P(deny\vert P/I \ ratio, black)} = \Phi (-\underset{(0.18)}{2.26} + \underset{(0.50)}{2.74} P/I \ ratio + \underset{(0.08)}{0.71} black). \tag{12.6} \end{align}\]
Si bien todos los coeficientes son muy significativos, tanto los coeficientes estimados de la relación pagos-ingresos como el indicador de ascendencia afroamericana son positivos. Nuevamente, los coeficientes son difíciles de interpretar pero indican que, en primer lugar, los afroamericanos tienen una mayor probabilidad de rechazo que los solicitantes blancos, manteniendo constante la proporción de pagos a ingresos y, en segundo lugar, los solicitantes con una alta proporción de pagos a ingresos enfrentan un mayor riesgo de ser rechazado.
¿Qué tan grande es la diferencia estimada en las probabilidades de denegación entre dos solicitantes hipotéticos con la misma proporción de pagos e ingresos? Como antes, se puede usar predict() para calcular esta diferencia.
# 1. Calcular predicciones para la relación P/I = 0.3
predictions <- predict(denyprobit2,
newdata = data.frame("black" = c("no", "yes"),
"pirat" = c(0.3, 0.3)),
type = "response")
# 2. Calcular la diferencia en probabilidades
diff(predictions)
#> 2
#> 0.1578117En este caso, la diferencia estimada en las probabilidades de negación es de aproximadamente \(15.8\%\).
Regresión Logit
El Concepto clave 11.3 resume la función de regresión Logit.
Concepto clave 11.3
Regresión Logit
La función de regresión Logit poblacional es
\[\begin{align*} P(Y=1\vert X_1, X_2, \dots, X_k) =& \, F(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k) \\ =& \, \frac{1}{1+e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k)}}. \end{align*}\]
La idea es similar a la regresión Probit, excepto que se usa un FDPA diferente: \[F(x) = \frac{1}{1+e^{-x}}\] es la FDPA de una variable aleatoria estándar distribuida logísticamente.
En cuanto a la regresión Probit, no existe una interpretación simple de los coeficientes del modelo y es mejor considerar las probabilidades pronosticadas o las diferencias en las probabilidades pronosticadas. Aquí nuevamente, las estadísticas de \(t\) y los intervalos de confianza basados en aproximaciones normales de muestras grandes se pueden calcular como de costumbre.
Es bastante fácil estimar un modelo de regresión Logit usando R.
denylogit <- glm(deny ~ pirat,
family = binomial(link = "logit"),
data = HMDA)
coeftest(denylogit, vcov. = vcovHC, type = "HC1")
#>
#> z test of coefficients:
#>
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -4.02843 0.35898 -11.2218 < 2.2e-16 ***
#> pirat 5.88450 1.00015 5.8836 4.014e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1El siguiente fragmento de código produce la gráfica.
# graficar datos
plot(x = HMDA$pirat,
y = HMDA$deny,
main = "Modelos Probit y Logit. Modelo de probabilidad de negación, relación P/I dada",
xlab = "Relación P / I",
ylab = "Denegar",
pch = 20,
ylim = c(-0.4, 1.4),
cex.main = 0.9)
# añadir texto y líneas discontinuas horizontales
abline(h = 1, lty = 2, col = "darkred")
abline(h = 0, lty = 2, col = "darkred")
text(2.5, 0.9, cex = 0.8, "Hipoteca negada")
text(2.5, -0.1, cex= 0.8, "Hipoteca aprobada")
# agregar una línea de regresión estimada de los modelos Probit y Logit
x <- seq(0, 3, 0.01)
y_probit <- predict(denyprobit, list(pirat = x), type = "response")
y_logit <- predict(denylogit, list(pirat = x), type = "response")
lines(x, y_probit, lwd = 1.5, col = "steelblue")
lines(x, y_logit, lwd = 1.5, col = "black", lty = 2)
# agrega una leyenda
legend("topleft",
horiz = TRUE,
legend = c("Probit", "Logit"),
col = c("steelblue", "black"),
lty = c(1, 2))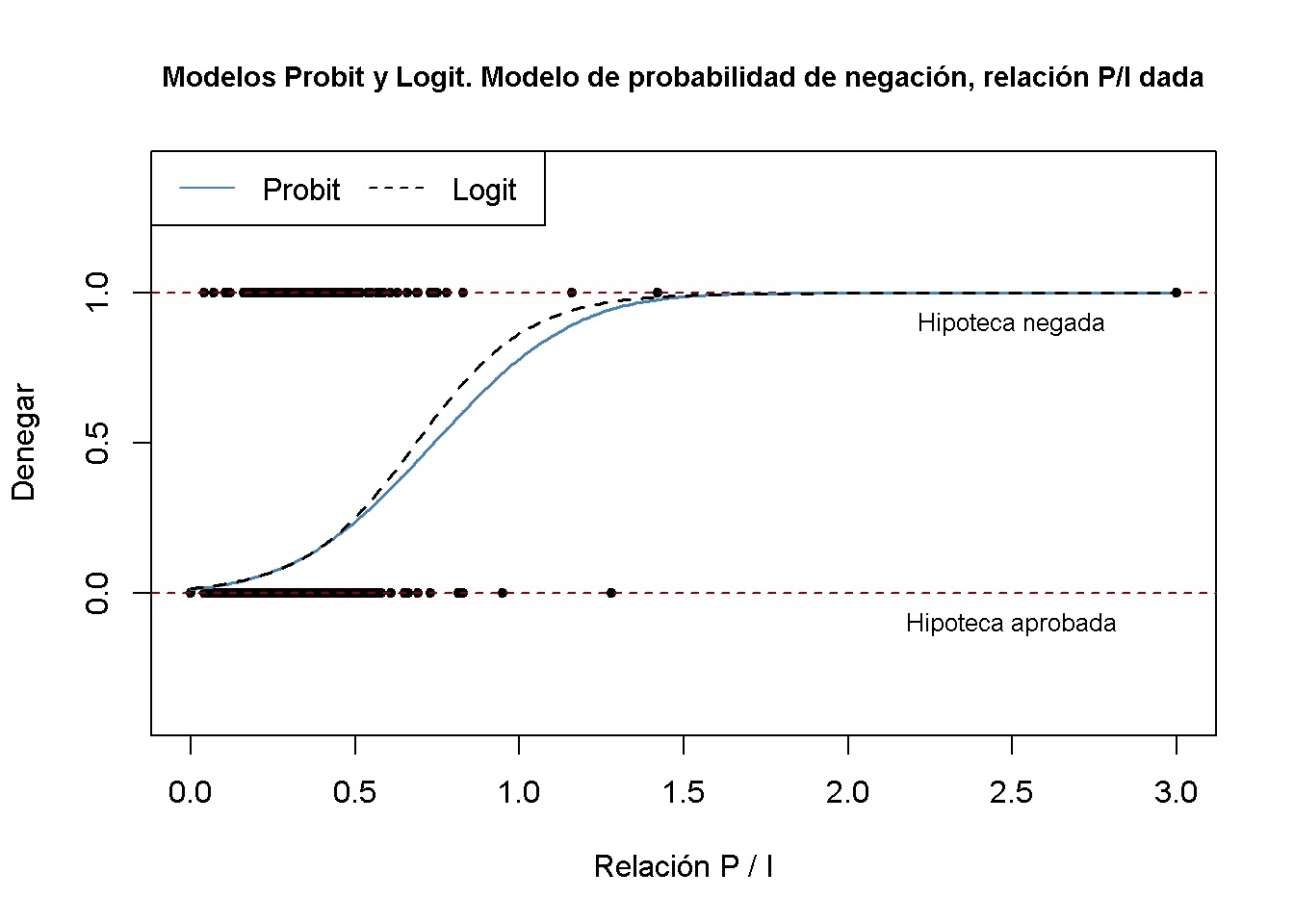
Ambos modelos producen estimaciones muy similares de la probabilidad de que una solicitud de hipoteca sea denegada dependiendo de la relación pago-ingresos del solicitante.
En este contexto, se amplia el modelo Logit simple de denegación de hipoteca con el regresor adicional \(black\).
# estimar una regresión Logit con múltiples regresores
denylogit2 <- glm(deny ~ pirat + black,
family = binomial(link = "logit"),
data = HMDA)
coeftest(denylogit2, vcov. = vcovHC, type = "HC1")
#>
#> z test of coefficients:
#>
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -4.12556 0.34597 -11.9245 < 2.2e-16 ***
#> pirat 5.37036 0.96376 5.5723 2.514e-08 ***
#> blackyes 1.27278 0.14616 8.7081 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Se obtiene
\[\begin{align} \widehat{P(deny=1 \vert P/I ratio, black)} = F(-\underset{(0.35)}{4.13} + \underset{(0.96)}{5.37} P/I \ ratio + \underset{(0.15)}{1.27} black). \tag{12.7} \end{align}\]
En cuanto al modelo Probit (12.6) todos los coeficientes del modelo son altamente significativos y se obtienen estimaciones positivas para los coeficientes en \(P/I \ ratio\) y \(black\). A modo de comparación, se calcula la probabilidad de rechazo prevista para dos solicitantes hipotéticos que difieren en la raza y tienen una relación \(P/I \ ratio\) de \(0.3\).
# 1. Calcular predicciones para la relación P/I = 0.3
predictions <- predict(denylogit2,
newdata = data.frame("black" = c("no", "yes"),
"pirat" = c(0.3, 0.3)),
type = "response")
predictions
#> 1 2
#> 0.07485143 0.22414592
# 2. Calcular la diferencia de probabilidades
diff(predictions)
#> 2
#> 0.1492945Se encuentra que el solicitante blanco enfrenta una probabilidad de denegación de solo \(7.5\%\), mientras que el afroamericano es rechazado con una probabilidad de \(22.4\%\), una diferencia de \(14.9\%\).
Comparación de los modelos
El modelo Probit y el modelo Logit ofrecen solo aproximaciones a la función de regresión de población desconocida \(E(Y\vert X)\). No es obvio cómo decidir qué modelo utilizar en la práctica. El modelo de probabilidad lineal tiene el claro inconveniente de no poder capturar la naturaleza no lineal de la función de regresión poblacional y puede predecir que las probabilidades se encuentren fuera del intervalo \([0,1]\). Los modelos Probit y Logit son más difíciles de interpretar, pero capturan las no linealidades mejor que el enfoque lineal: Ambos modelos producen predicciones de probabilidades que se encuentran dentro del intervalo \([0,1]\). Las predicciones de los tres modelos suelen estar próximas entre sí. El libro sugiere utilizar el método que sea más fácil de usar en el software estadístico de su elección. Como se ha visto, es igualmente fácil estimar el modelo Probit y Logit usando R. Por lo tanto, no se puede dar ninguna recomendación general sobre qué método utilizar.