3.2 Muestreo aleatorio y distribución de promedios muestrales
Para aclarar la idea básica del muestreo aleatorio, volviendo al ejemplo de tirar los dados:
Suponga que se tirando los dados \(n\) veces. Esto significa que se está interesado en los resultados aleatorios de \(Y_i\), \(i = 1, ..., n\) que se caracterizan por la misma distribución. Dado que estos resultados se seleccionan al azar, son variables aleatorias en sí mismas y sus resultados diferirán cada vez que se extraiga una muestra; es decir, cada vez que se tiren los dados \(n\) veces. Además, cada observación se extrae aleatoriamente de la misma población; es decir, los números de \(1\) hasta \(6\), y su distribución individual es la misma. Por tanto, \(Y_1, \dots, Y_n\) se distribuyen de forma idéntica.
Además, se sabe que el valor de cualquiera de los \(Y_i\) no proporciona ninguna información sobre el resto de los resultados. En el ejemplo, sacar un seis como la primera observación en la muestra no altera las distribuciones de \(Y_2, \dots , Y_n\): Todos los números tienen la misma probabilidad de ocurrir. Esto significa que todos los \(Y_i\) también se distribuyen de forma independiente. Por tanto, \(Y_1, \dots, Y_n\) son independientes e idénticamente distribuidos (i.i.d).
El ejemplo de los dados usa este esquema de muestreo más simple. Por eso se llama muestreo aleatorio simple. Este concepto se resume en el Concepto clave 2.5.
Concepto clave 2.5
Muestreo aleatorio simple y Variables aleatorias independientes e idénticamente distribuidas (i.i.d)
En un muestreo aleatorio simple, \(n\) objetos se extraen al azar de una población. Es igualmente probable que cada objeto termine en la muestra. Se denota el valor de la variable aleatoria \(Y\) para el objeto \(i^{th}\) dibujado al azar como \(Y_i\). Dado que todos los objetos tienen la misma probabilidad de ser tomados y la distribución de \(Y_i\) es la misma para todos los \(i\), los \(Y_i, \dots, Y_n\) son independientes e idénticamente distribuidos (i.i.d.). Esto significa que la distribución de \(Y_i\) es la misma para todos los \(i=1,\dots,n\) y \(Y_1\) se distribuyen independientemente de \(Y_2, \dots, Y_n\) y \(Y_2\) se distribuyen independientemente de \(Y_1, Y_3, \dots, Y_n\) y así sucesivamente.
¿Qué sucede si se consideran funciones de los datos de la muestra? Considere, una vez más, el ejemplo de lanzar un dado dos veces seguidas. Una muestra ahora consta de dos extracciones aleatorias independientes del conjunto \(\{1,2,3,4,5,6\}\). Es evidente que cualquier función de estas dos variables aleatorias también es aleatoria; por ejemplo, su suma. Convénzase ejecutando el siguiente código varias veces.
sum(sample(1:6, 2, replace = T))
#> [1] 7Claramente, esta suma, llamada \(S\), es una variable aleatoria, dado que depende de sumandos extraídos aleatoriamente. Para este ejemplo, se pueden enumerar completamente todos los resultados y, por lo tanto, escribir la distribución de probabilidad teórica de la función de los datos de la muestra \(S\):
En esta situación se está enfrentando a \(6^2 = 36\) pares posibles. Esos pares son:
\[\begin{align*} &(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) \\ &(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) \\ &(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) \\ &(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) \\ &(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) \\ &(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) \end{align*}\]
Por lo tanto, los posibles resultados para \(S\) son:
\[ \left\{ 2,3,4,5,6,7,8,9,10,11,12 \right\} . \]
Enumeración de rendimientos de los resultados:
\[\begin{align} P(S) = \begin{cases} 1/36, \ & S = 2 \\ 2/36, \ & S = 3 \\ 3/36, \ & S = 4 \\ 4/36, \ & S = 5 \\ 5/36, \ & S = 6 \\ 6/36, \ & S = 7 \\ 5/36, \ & S = 8 \\ 4/36, \ & S = 9 \\ 3/36, \ & S = 10 \\ 2/36, \ & S = 11 \\ 1/36, \ & S = 12 \end{cases} \end{align}\]
También se puede calcular \(E(S)\) y \(\text{Var}(S)\) como se indica en el Concepto clave 2.1 y el Concepto clave 2.2.
# Vector de resultados
S <- 2:12
# Vector de probabilidades
PS <- c(1:6, 5:1) / 36
# Expectativa de S
ES <- sum(S * PS)
ES
#> [1] 7
# Varianza de S
VarS <- sum((S - c(ES))^2 * PS)
VarS
#> [1] 5.833333Entonces se conoce la distribución de \(S\). También es evidente que su distribución difiere considerablemente de la distribución marginal; es decir, la distribución del resultado de una sola tirada de dados, \(D\). Se puede visualizar esto usando gráficos de barras.
# divide el área de trazado en una fila con dos columnas
par(mfrow = c(1, 2))
# graficar la distribución de S
barplot(PS,
ylim = c(0, 0.2),
xlab = "S",
ylab = "Probabilidad",
col = "steelblue",
space = 0,
main = "Suma de dos lanzamientos")
# graficar la distribución de D
probability <- rep(1/6, 6)
names(probability) <- 1:6
barplot(probability,
ylim = c(0, 0.2),
xlab = "D",
col = "steelblue",
space = 0,
main = "Resultado de un solo lanzamiento")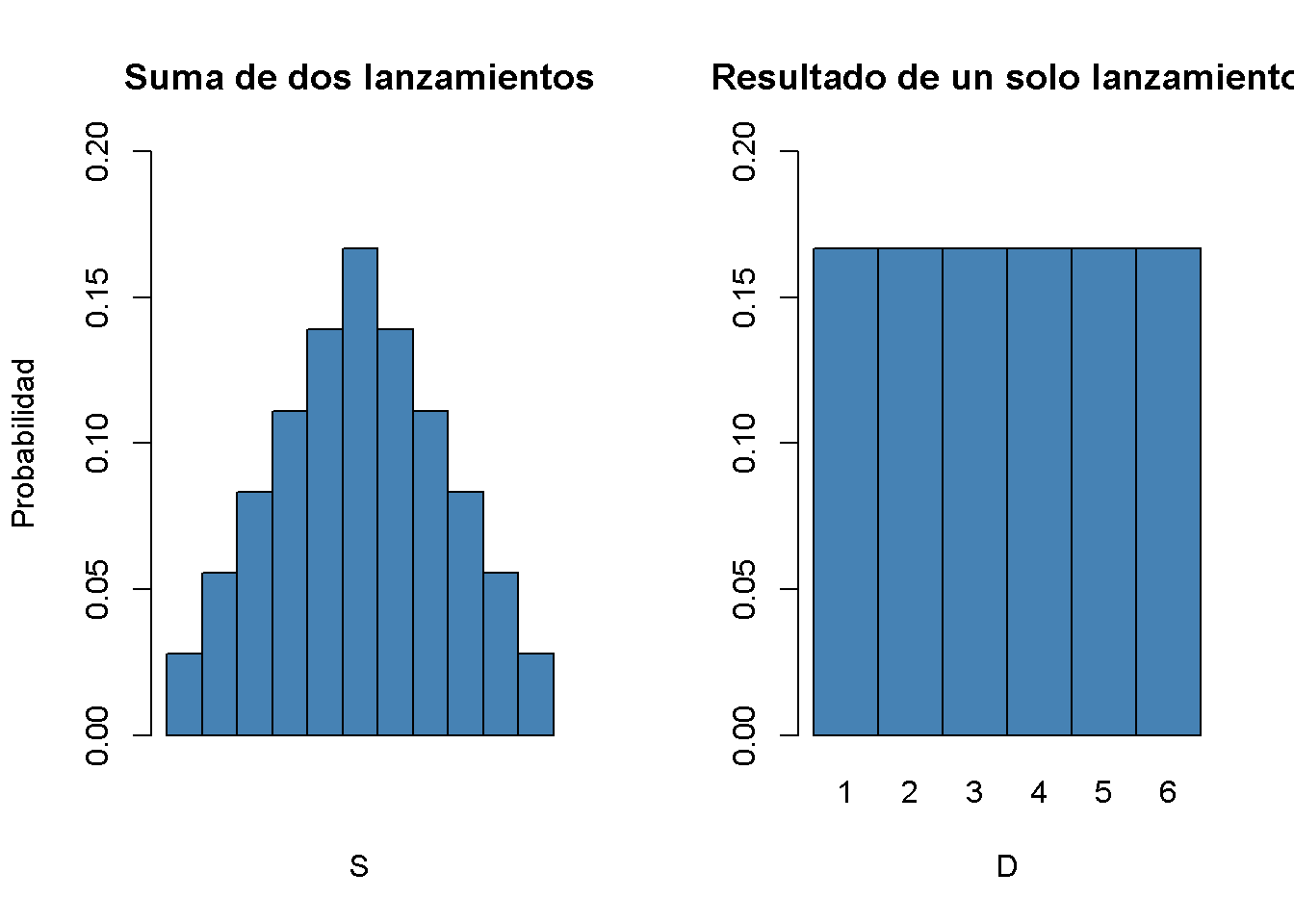
Muchos procedimientos econométricos tratan con promedios de datos muestreados. Por lo general, se asume que las observaciones se extraen al azar de una población desconocida más grande. Como se demostró para la función de muestra \(S\), calcular el promedio de una muestra aleatoria tiene el efecto de que el promedio es una variable aleatoria en sí misma. Dicha variable aleatoria, a su vez, tiene una distribución de probabilidad, denominada distribución de muestreo. Por tanto, el conocimiento sobre la distribución muestral del promedio es fundamental para comprender el desempeño de los procedimientos econométricos.
El promedio de la muestra de una muestra de \(n\) observaciones \(Y_1, \dots, Y_n\) es
\[ \overline{Y} = \frac{1}{n} \sum_{i=1}^n Y_i = \frac{1}{n} (Y_1 + Y_2 + \cdots + Y_n). \]
\(\overline{Y}\) también se denomina media muestral.
Media y varianza de la media muestral
Suponga que \(Y_1,\dots,Y_n\) son i.i.d. y se denota \(\mu_Y\) y \(\sigma_Y^2\) como la media y la varianza de \(Y_i\). Entonces se tiene que:
\[ E(\overline{Y}) = E\left(\frac{1}{n} \sum_{i=1}^n Y_i \right) = \frac{1}{n} E\left(\sum_{i=1}^n Y_i\right) = \frac{1}{n} \sum_{i=1}^n E\left(Y_i\right) = \frac{1}{n} \cdot n \cdot \mu_Y = \mu_Y \]
y
\[\begin{align*} \text{Var}(\overline{Y}) =& \text{Var}\left(\frac{1}{n} \sum_{i=1}^n Y_i \right) \\ =& \frac{1}{n^2} \sum_{i=1}^n \text{Var}(Y_i) + \frac{1}{n^2} \sum_{i=1}^n \sum_{j=1, j\neq i}^n \text{cov}(Y_i,Y_j) \\ =& \frac{\sigma^2_Y}{n} \\ =& \sigma_{\overline{Y}}^2. \end{align*}\]
El segundo sumando desaparece desde \(\text{cov}(Y_i,Y_j)=0\) para \(i\neq j\) debido a la independencia. En consecuencia, la desviación estándar de la media muestral viene dada por
\[\sigma_{\overline{Y}} = \frac{\sigma_Y}{\sqrt{n}}.\]
Vale la pena mencionar que estos resultados se mantienen independientemente de la distribución subyacente de \(Y_i\).
La distribución de muestreo de \(\overline{Y}\) cuando \(Y\) se distribuye normalmente
Si \(Y_1,\dots,Y_n\) son i.i.d. se extrae de una distribución normal con media \(\mu_Y\) y varianza \(\sigma_Y^2\), lo siguiente es válido para su promedio de muestra \(\overline{Y}\):
\[ \overline{Y} \sim \mathcal{N}(\mu_Y, \sigma_Y^2/n) \tag{2.4} \]
Por ejemplo, si una muestra \(Y_i\) con \(i=1,\dots,10\) se extrae de una distribución normal estándar con media \(\mu_Y = 0\) y varianza \(\sigma_Y^2=1\) se sigue que:
\[ \overline{Y} \sim \mathcal{N}(0,0.1).\]
Se puede usar la instalación de generación de números aleatorios de R para verificar el resultado. La idea básica es simular los resultados de la distribución real de \(\overline{Y}\) extrayendo repetidamente muestras aleatorias de 10 observaciones de la distribución \(\mathcal{N}(0,1)\) y calculando sus respectivos promedios. Si se hace esto para un gran número de repeticiones, el conjunto de datos simulados de promedios debería reflejar con bastante precisión la distribución teórica de \(\overline{Y}\) si el resultado teórico se cumple.
El enfoque esbozado anteriormente es un ejemplo de lo que se conoce comúnmente como Simulación de Monte Carlo o Experimento de Monte Carlo. Para realizar esta simulación en R se debe proceder de la siguiente manera:
Elegir un tamaño de muestra n y el número de muestras que se extraerán, reps.
Utilizar la función replicate() junto con rnorm() para extraer n observaciones de la distribución normal estándar rep veces.
Nota: El resultado de replicate() es una matriz con dimensiones n \(\times\) rep. Contiene las muestras extraídas como columnas.
Calcular las medias de la muestra utilizando colMeans(). Esta función calcula la media de cada columna; es decir, de cada muestra y devuelve un vector.
# establecer el tamaño de la muestra y el número de muestras
n <- 10
reps <- 10000
# realizar muestreo aleatorio
muestras <- replicate(reps, rnorm(n)) # 10 x 10000 sample matrix
# calcular medias de muestra
muestra.promedios <- colMeans(muestras)Luego se termina con un vector de promedios muestrales (medias muestrales). Se puede verificar la propiedad vectorial de muestra.promedios:
# comprobar que 'muestra.promedios' es un vector
is.vector(muestra.promedios)
#> [1] TRUE
# imprimir las primeras entradas en la consola
head(muestra.promedios)
#> [1] -0.1045919 0.2264301 0.5308715 -0.2243476 0.2186909 0.2564663Un enfoque sencillo para examinar la distribución de datos numéricos univariados es trazarlos como un histograma y compararlos con alguna distribución conocida o supuesta. De forma predeterminada, hist() da un histograma de frecuencia; es decir, un gráfico de barras donde las observaciones se agrupan en rangos, también llamados bins. La ordenada informa el número de observaciones que caen en cada uno de los contenedores. En cambio, se quiere que informe estimaciones de densidad con fines de comparación. Esto se logra estableciendo el argumento freq = FALSE. El número de bins se ajusta mediante el argumento breaks.
Usando curve(), se superpone el histograma con una línea roja, la densidad teórica de una variable aleatoria \(\mathcal{N}(0, 0.1)\) . Recuerde usar el argumento add = TRUE para agregar la curva al gráfico actual. De lo contrario, R abrirá un nuevo dispositivo gráfico y descartará el gráfico anterior.1
# Grafique el histograma de densidad
hist(muestra.promedios,
ylim = c(0, 1.4),
col = "steelblue" ,
freq = F,
breaks = 20)
# Superponga la distribución teórica de los promedios de la muestra en la parte superior del histograma
curve(dnorm(x, sd = 1/sqrt(n)),
col = "red",
lwd = "2",
add = T)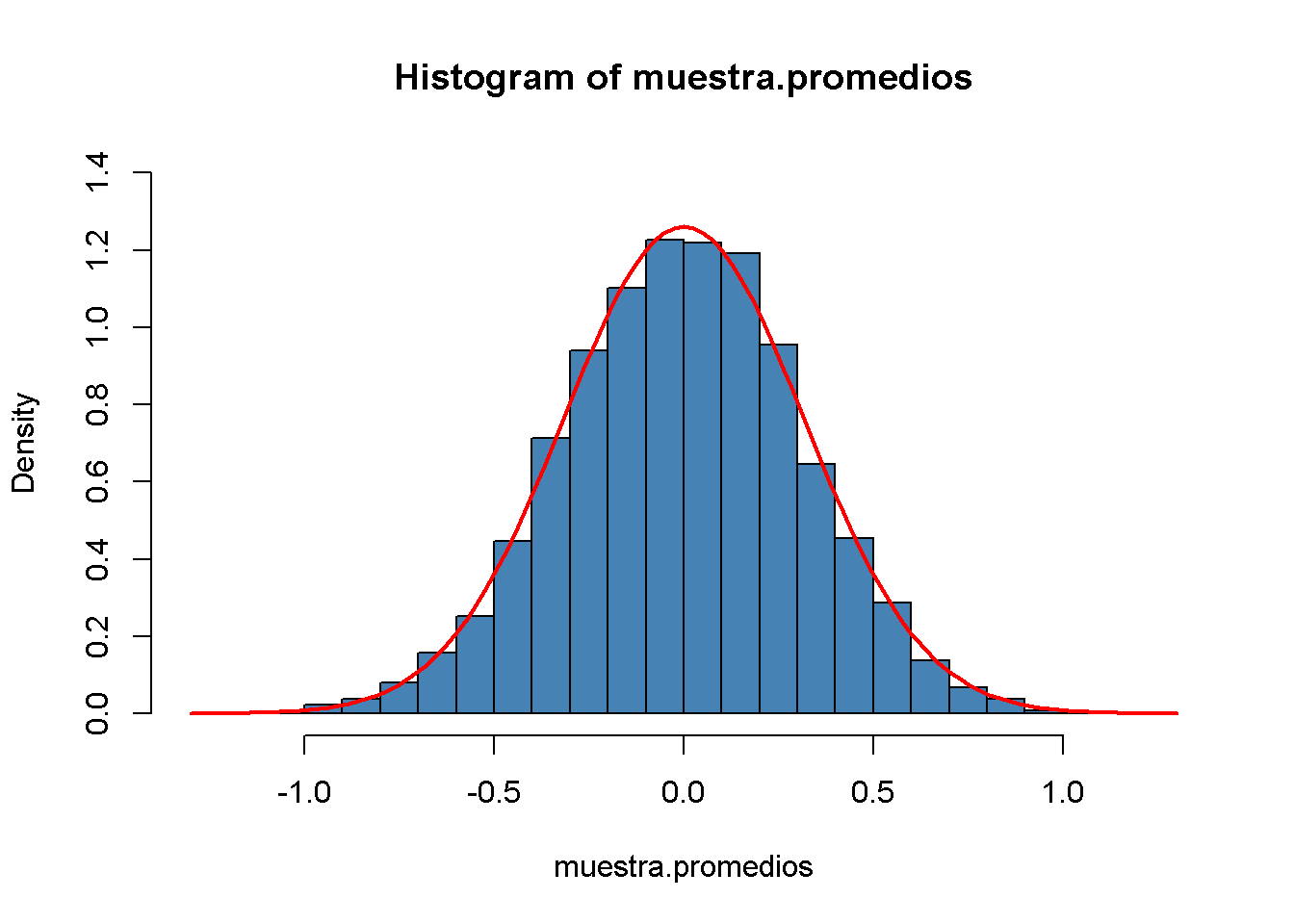
La distribución de muestreo de \(\overline{Y}\) es, de hecho, muy cercana a la de una distribución \(\mathcal{N}(0, 0.1)\), por lo que la simulación de Monte Carlo respalda la afirmación teórica.
Analizando otro ejemplo en que el uso del muestreo aleatorio simple en una configuración de simulación ayuda a verificar un resultado bien conocido. Como se discutió antes, la distribución Chi-cuadrado con \(M\) grados de libertad surge como la distribución de la suma de \(M\) variables aleatorias independientes distribuidas de forma normalmente estándar al cuadrado.
Para visualizar el argumento expresado en la ecuación (2.3), se procede de manera similar al ejemplo anterior:
- Elija los grados de libertad, DF (Degrees of Freedom) y el número de muestras que se extraerán repeticiones.
- Graficar las reps de las muestras aleatorias de tamaño DF de la distribución normal estándar usando replicate().
- Para cada muestra, potencie los resultados al cuadrado y súmelos en columnas. Almacene los resultados.
Nuevamente, se produce una estimación de densidad para la distribución subyacente a los datos simulados usando un histograma de densidad y se superpone con un gráfico lineal de la función de densidad teórica de la distribución \(\chi^2_3\).
# número de repeticiones
reps <- 10000
# establecer grados de libertad de una distribución chi-cuadrada
DF <- 3
# muestra 10000 vectores de columna à 3 N (0,1) R.V.S
Z <- replicate(reps, rnorm(DF))
# columna sumas de cuadrados
X <- colSums(Z^2)
# histograma de columnas de sumas de cuadrados
hist(X,
freq = F,
col = "steelblue",
breaks = 40,
ylab = "Densidad",
main = "")
# agregar densidad teórica
curve(dchisq(x, df = DF),
type = 'l',
lwd = 2,
col = "red",
add = T)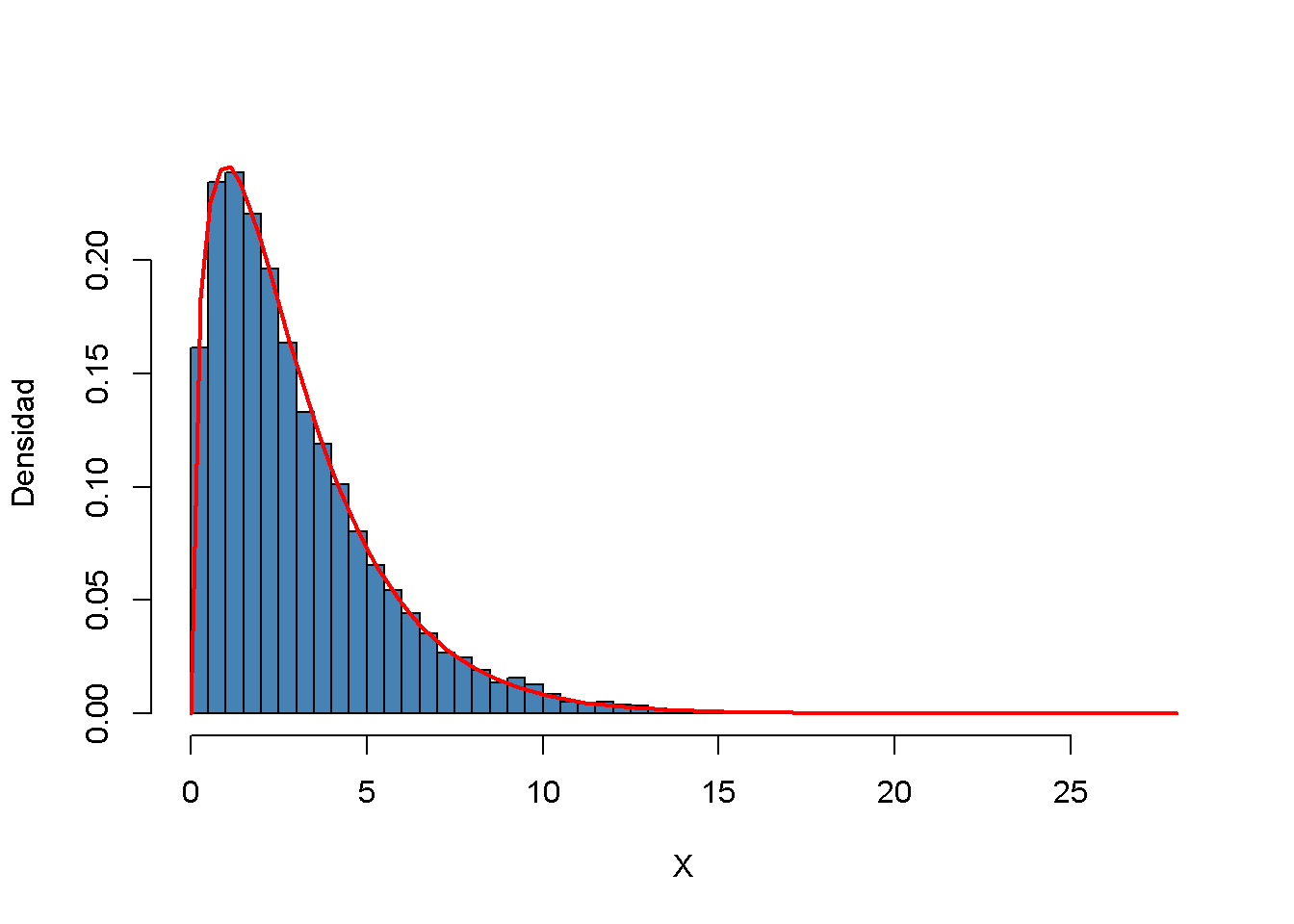
Aproximaciones de muestras grandes para distribuciones de muestreo
Las distribuciones muestrales consideradas en la última sección juegan un papel importante en el desarrollo de métodos econométricos. Existen dos enfoques principales para caracterizar las distribuciones muestrales: Un enfoque “exacto” y un enfoque “aproximado.”
El enfoque exacto tiene como objetivo encontrar una fórmula general para la distribución muestral, que se mantiene para cualquier tamaño de muestra \(n\). A esto se le llama distribución exacta o distribución de muestra finita. En los ejemplos anteriores de lanzamiento de dados y variantes normales, se ha tratado con funciones de variables aleatorias cuyas distribuciones de muestra son exactamente conocidas en el sentido de que se pueden escribir como expresiones analíticas. Sin embargo, esto no siempre es posible. Para \(\overline{Y}\), el resultado (2.4) indica que la normalidad de \(Y_i\) implica la normalidad de \(\overline{Y}\) (se demuestra esto para el caso especial de \(Y_i \overset{i.i.d.}{\sim} \mathcal{N}(0,1)\) con \(n=10\) usando un estudio de simulación que involucra un muestreo aleatorio simple). Desafortunadamente, la distribución exacta de \(\overline{Y}\) es generalmente desconocida y, a menudo, difícil de derivar (o incluso imposible de rastrear) si se descarta la suposición de que \(Y_i\) tiene una distribución normal.
Por lo tanto, como se puede adivinar por su nombre, el enfoque “aproximado” tiene como objetivo encontrar una aproximación a la distribución muestral donde se requiere que el tamaño de la muestra \(n\) sea grande. Una distribución que se utiliza como una aproximación de muestra grande a la distribución muestral también se denomina distribución asintótica. Esto se debe al hecho de que la distribución asintótica es la distribución de muestreo para \(n \rightarrow \infty\); es decir, la aproximación se vuelve exacta si el tamaño de la muestra llega al infinito. Sin embargo, la diferencia entre la distribución muestral y la distribución asintótica es insignificante para tamaños de muestra moderados o incluso pequeños, por lo que las aproximaciones que utilizan la distribución asintótica son útiles.
En esta sección se discurtirán dos resultados bien conocidos que se utilizan para aproximar distribuciones muestrales y, por lo tanto, constituyen herramientas clave en la teoría econométrica: la ley de los grandes números y el teorema del límite central. La ley de los números grandes establece que en muestras grandes, \(\overline{Y}\) está cerca de \(\mu_Y\) con alta probabilidad. El teorema del límite central dice que la distribución muestral de los promedios muestrales estandarizados; es decir, \((\overline{Y} - \mu_Y)/\sigma_{\overline{Y}}\) tiene una distribución asintóticamente normal. Es particularmente interesante que ambos resultados no dependen de la distribución de \(Y\). En otras palabras, al no poder describir la complicada distribución muestral de \(\overline{Y}\) si \(Y\) no es normal, las aproximaciones de este último utilizando el teorema del límite central simplifican enormemente el desarrollo y la aplicabilidad de los procedimientos econométricos. Este es un componente clave que subyace a la teoría de la inferencia estadística para modelos de regresión. Ambos resultados se resumen en el Concepto clave 2.6 y el Concepto clave 2.7.
Concepto clave 2.6
Convergencia en probabilidad, consistencia y la ley de los números grandes
El promedio de la muestra \(\overline{Y}\) converge en probabilidad a \(\mu_Y\): \(\overline{Y}\) es consistente para \(\mu_Y\) si la probabilidad de que \(\overline{Y}\) está en el rango \((\mu_Y - \epsilon)\) a \((\mu_Y + \epsilon)\) se vuelve arbitrario cerca de \(1\) a medida que \(n\) aumenta para cualquier \(\epsilon > 0\). Se escribe esto como:
\[ P(\mu_Y-\epsilon \leq \overline{Y} \leq \mu_Y + \epsilon) \rightarrow 1, \, \epsilon > 0 \text{ as } n\rightarrow\infty. \]
Considere las variables aleatorias distribuidas de forma independiente e idéntica \(Y_i, i=1,\dots,n\) con expectativa \(E(Y_i)=\mu_Y\) y varianza \(\text{Var}(Y_i)=\sigma^2_Y\). Bajo la condición de que \(\sigma^2_Y< \infty\); es decir, los valores atípicos grandes son poco probables, la ley de los números grandes establece que
\[ \overline{Y} \xrightarrow[]{p} \mu_Y. \]
La siguiente aplicación simula una gran cantidad de lanzamientos de monedas (puede establecer el número de intentos usando el control deslizante) con una moneda justa. Asimismo, calcula la fracción de caras observadas para cada lanzamiento adicional. El resultado es una ruta aleatoria que, como lo establece la ley de los números grandes, muestra una tendencia a acercarse al valor de \(0.5\) a medida que \(n\) crece.
El enunciado central de la ley de los grandes números es que, en condiciones bastante generales, la probabilidad de obtener un promedio de muestra \(\overline{Y}\) que esté cerca de \(\mu_Y\) es alta si se tiene un tamaño de muestra grande.
Al considerar el ejemplo de lanzar repetidamente una moneda donde \(Y_i\) es el resultado del lanzamiento de la moneda \(i^{th}\). \(Y_i\) es una variable aleatoria distribuida de Bernoulli con \(p\) la probabilidad de observar la cara
\[ P(Y_i) = \begin{cases} p, & Y_i = 1 \\ 1-p, & Y_i = 0 \end{cases} \]
donde \(p = 0.5\) como se asume una moneda justa. Es sencillo demostrar que
\[ \mu_Y = p = 0.5. \]
Sea \(R_n\) la proporción de caras en los primeros \(n\) lanzamientos,
\[ R_n = \frac{1}{n} \sum_{i=1}^n Y_i. \tag{2.5}\]
De acuerdo con la ley de los números grandes, la proporción observada de caras converge en probabilidad a \(\mu_Y = 0.5\), la probabilidad de lanzar cara en un solo lanzamiento de moneda,
\[ R_n \xrightarrow[]{p} \mu_Y=0.5 \ \ \text{as} \ \ n \rightarrow \infty.\]
Este resultado es ilustrado por la aplicación interactiva en el Concepto clave 2.6. Ahora se debe demostrar cómo replicar esto usando R.
El procedimiento es el siguiente:
Muestra de N observaciones de la distribución de Bernoulli, por ejemplo, usar sample().
Calcular la proporción de caras \(R_n\) como en (2.5). Una forma de lograr esto es llamar a cumsum() en el vector de observaciones Y para obtener su suma acumulada y luego dividir por el número respectivo de observaciones.
Se continua trazando la ruta y también agregando una línea discontinua para la probabilidad de referencia \(p = 0.5\).
# sembrar semilla
set.seed(1)
# establecer el número de lanzamientos de monedas y simular
N <- 30000
Y <- sample(0:1, N, replace = T)
# calcular R_n para 1: N
S <- cumsum(Y)
R <- S/(1:N)
# graficar el camino
plot(R,
ylim = c(0.3, 0.7),
type = "l",
col = "steelblue",
lwd = 2,
xlab = "n",
ylab = "R_n",
main = "Cuota convergente de caras en el lanzamiento repetido de monedas")
# agregar una línea discontinua para R_n = 0.5
lines(c(0, N),
c(0.5, 0.5),
col = "darkred",
lty = 2,
lwd = 1)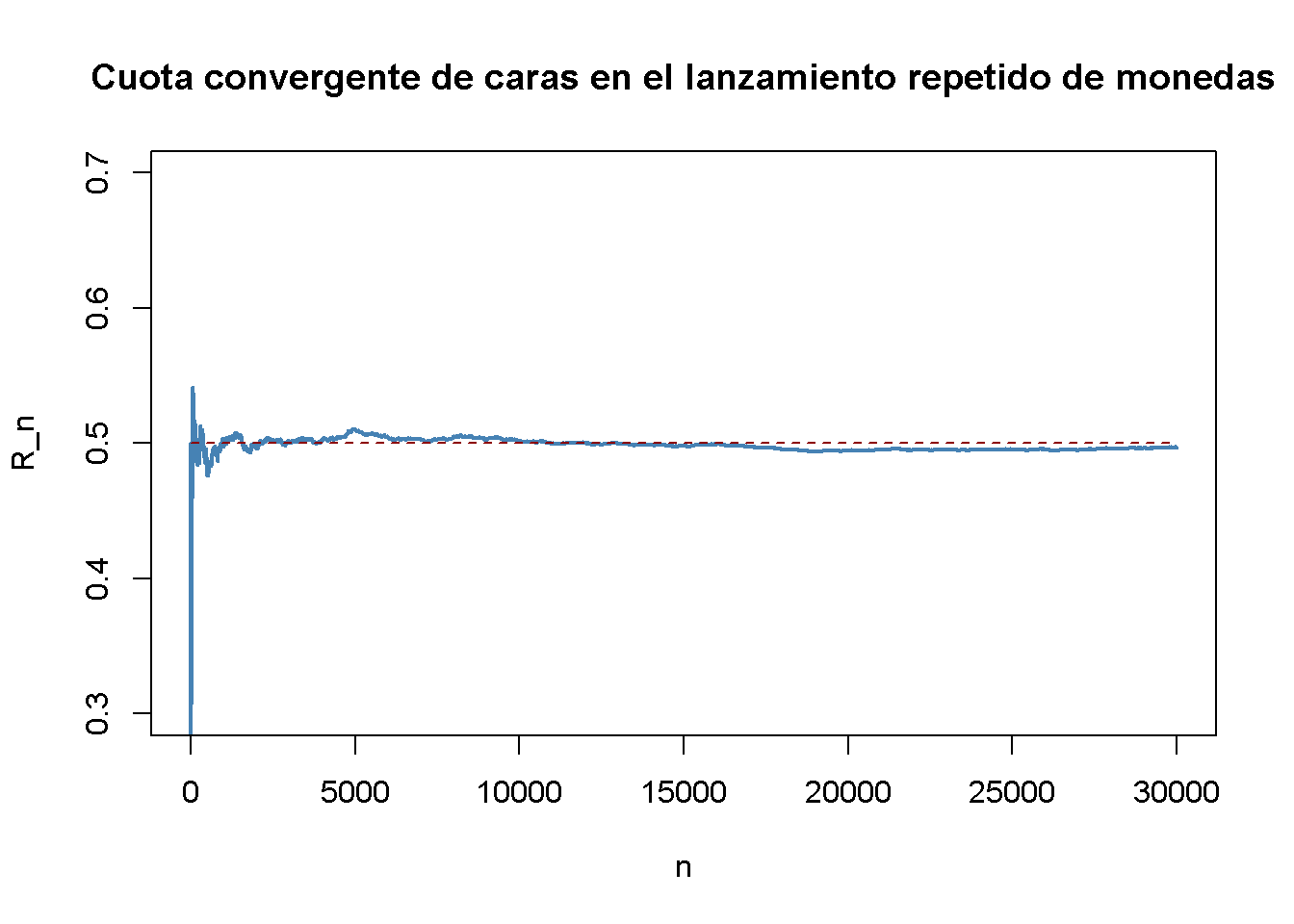
Hay varias cosas que decir sobre esta trama.
El gráfico azul muestra la proporción observada de caras al lanzar una moneda \(n\) veces.
Dado que \(Y_i\) son variables aleatorias, \(R_n\) también es una variable aleatoria. La ruta representada es solo una de las muchas realizaciones posibles de \(R_n\), ya que está determinada por las observaciones de \(30000\) muestreadas de la distribución de Bernoulli.
Si el número de lanzamientos de moneda \(n\) es pequeño, la proporción de caras puede ser cualquier cosa menos cercana a su valor teórico, \(\mu_Y = 0.5\). Sin embargo, a medida que se incluyen más y más observaciones en la muestra, se encuentra que la trayectoria se estabiliza en el vecindario de \(0.5\). El promedio de múltiples ensayos muestra una clara tendencia a converger a su valor esperado a medida que aumenta el tamaño de la muestra, tal como lo afirma la ley de los grandes números.
Concepto clave 2.7
El teorema del límite central
Suponga que \(Y_1,\dots,Y_n\) son variables aleatorias independientes y distribuidas de forma idéntica con expectativa \(E(Y_i)=\mu_Y\) y varianza \(\text{Var}(Y_i)=\sigma^2_Y\) donde \(0<\sigma^2_Y<\infty\). El Teorema del Límite Central (TLC) establece que, si el tamaño de la muestra \(n\) llega al infinito, la distribución del promedio muestral estandarizado
\[ \frac{\overline{Y} - \mu_Y}{\sigma_{\overline{Y}}} = \frac{\overline{Y} - \mu_Y}{\sigma_Y/\sqrt{n}} \ \]
se aproxima arbitrariamente bien por la distribución normal estándar.
La siguiente aplicación demuestra el TLC para el promedio de la muestra de variables aleatorias distribuidas normalmente con una media de \(5\) y una varianza de \(25^2\). Se pueden comprobar las siguientes propiedades:
- La distribución del promedio de la muestra es normal.
- A medida que aumenta el tamaño de la muestra, la distribución de \(\overline{Y}\) se ajusta alrededor de la media real de \(5\).
- La distribución del promedio muestral estandarizado está cerca de la distribución normal estándar para grandes \(n\).
Según el TLC, la distribución de la media muestral \(\overline{Y}\) de las variables aleatorias distribuidas de Bernoulli \(Y_i\), \(i=1,...,n\), está bien aproximada por la distribución normal con parámetros \(\mu_Y=p=0.5\) y \(\sigma^2_{Y} = p(1-p)/n = 0.25/n\) para \(n\) grandes. En consecuencia, para la media muestral estandarizada, se llega a la conclusión de que
\[\frac{\overline{Y} - 0.5}{0.5/\sqrt{n}} \tag{2.6}\]
debería estar bien aproximado por la distribución normal estándar \(\mathcal{N}(0,1)\). Se emplea otro estudio de simulación para demostrar esto gráficamente. La idea es la siguiente.
Extraiga una gran cantidad de muestras aleatorias, suponiendo \(10000\), de tamaño \(n\) de la distribución de Bernoulli y calcular los promedios de las muestras. Estandarizar los promedios como se muestra en (2.6). A continuación, visualizar la distribución de los promedios muestrales estandarizados generados por medio de un histograma y comparar con la distribución normal estándar. Repetir esto para diferentes tamaños de muestra \(n\) para ver cómo el aumento del tamaño de muestra \(n\) afecta la distribución simulada de los promedios.
En R, se puede dar cuenta de esto de la siguiente manera:
Comenzar por definir que las siguientes cuatro figuras generadas posteriormente se dibujarán en una matriz \(2\times2\) de manera que puedan compararse fácilmente. Esto se hace llamando a
par(mfrow = c(2, 2))antes de generar las figuras.Definir el número de repeticiones reps como \(10000\) y crear un vector de tamaños de muestra llamado sample.sizes. Considerar muestras de tamaños de \(5\), \(20\), \(75\) y \(100\).
A continuación, combinar dos bucles for() para simular los datos y graficar las distribuciones. El ciclo interno genera muestras aleatorias de \(10000\), cada una de las cuales consta de n observaciones que se extraen de la distribución de Bernoulli, y calcula los promedios estandarizados. El ciclo externo ejecuta el ciclo interno para los diferentes tamaños de muestra n y produce una gráfica para cada iteración.
# subdividir el panel de la trama en una matriz de 2 por 2
par(mfrow = c(2, 2))
# establecer el número de repeticiones y los tamaños de muestra
reps <- 10000
sample.sizes <- c(5, 20, 75, 100)
# sembrar la semilla para la reproducibilidad
set.seed(123)
# bucle externo (bucle sobre los tamaños de muestra)
for(n in sample.sizes){
samplemean <- rep(0, reps) # inicializar el vector de medias muestrales
stdsamplemean <- rep(0, reps) # inicializar el vector de medias muestrales estandarizadas
# bucle interno (bucle sobre repeticiones)
for(i in 1:reps){
x <- rbinom(n, 1, 0.5)
samplemean[i] <- mean(x)
stdsamplemean[i] <- sqrt(n)*(mean(x) - 0.5)/0.5
}
# graficar el histograma y superponer la densidad N(0,1) en cada iteración
hist(stdsamplemean,
col = "steelblue",
freq = FALSE,
breaks = 40,
xlim = c(-3, 3),
ylim = c(0, 0.8),
xlab = paste("n =", n),
main = "")
curve(dnorm(x),
lwd = 2,
col = "darkred",
add = TRUE)
} 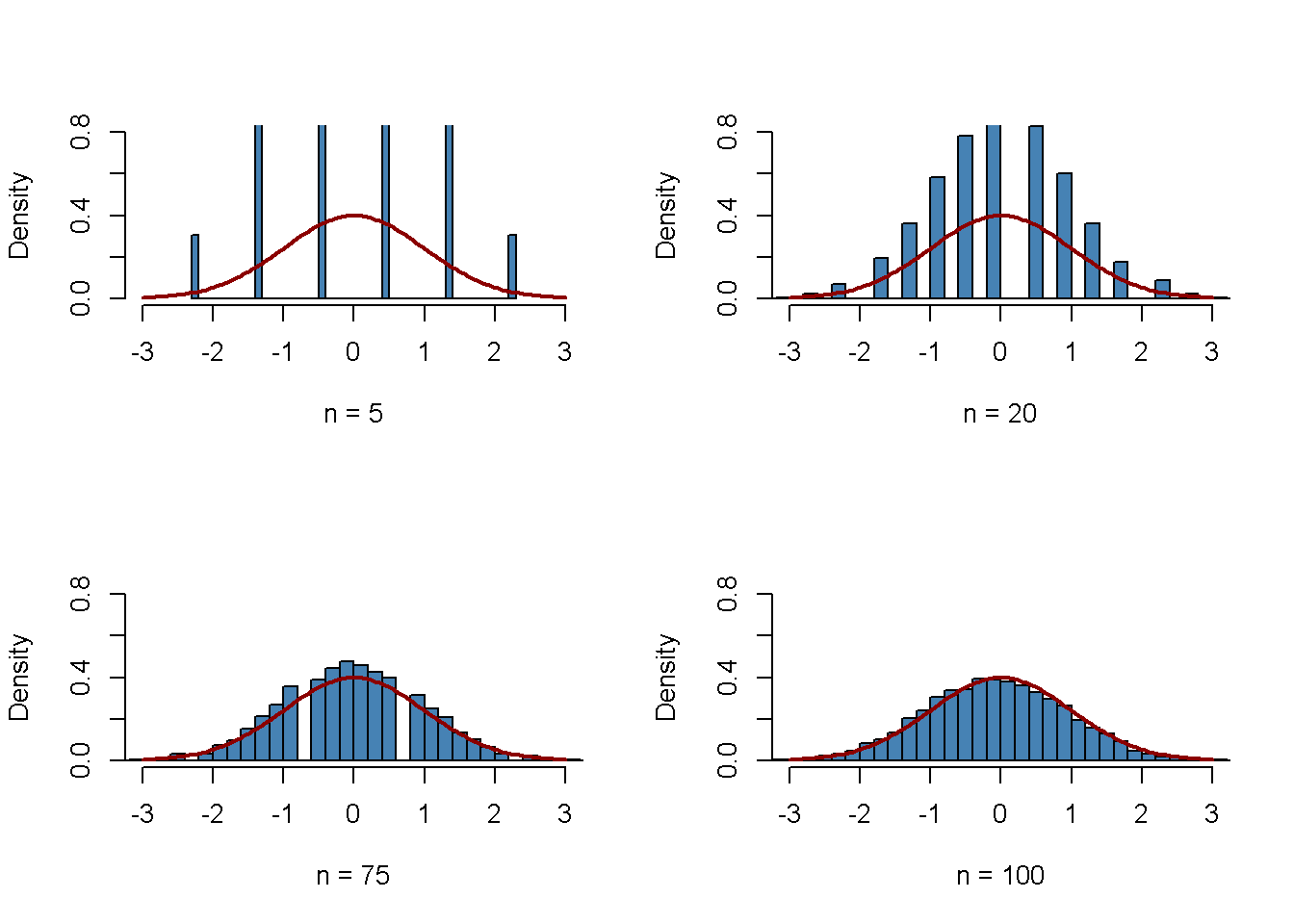
Se puede ver que la distribución muestral simulada del promedio estandarizado tiende a desviarse fuertemente de la distribución normal estándar si el tamaño de la muestra es pequeño, por ejemplo, para \(n = 5\) y \(n = 10\). Sin embargo, a medida que crece \(n\), los histogramas se acercan a la distribución normal estándar. La aproximación funciona bastante bien, vea \(n = 100\).
Sugerencia: T y F son alternativas para TRUE y FALSE.↩︎