6.4 Heteroscedasticidad y homocedasticidad
Todas las inferencias hechas en los capítulos anteriores se basan en el supuesto de que la varianza del error no varía a medida que cambian los valores del regresor. Pero este no suele ser el caso en las aplicaciones empíricas.
Concepto clave 5.4
Heteroscedasticidad y homocedasticidad
- El término de error del modelo de regresión es homocedástico si la varianza de la distribución condicional de \(u_i\) dado \(X_i\), \(Var(u_i|X_i=x)\), es constante para todas las observaciones en la muestra:
\[ \text{Var}(u_i|X_i=x) = \sigma^2 \ \forall \ i=1,\dots,n. \]
- Si, en cambio, existe dependencia de la varianza condicional de \(u_i\) con \(X_i\), se dice que el término de error es heterocedástico. Luego se escribe:
\[ \text{Var}(u_i|X_i=x) = \sigma_i^2 \ \forall \ i=1,\dots,n. \]
- La homocedasticidad es un caso especial de heterocedasticidad. En conclusión, en los modelos de regresión lineales se dice que hay heterocedasticidad cuando la varianza de los errores no es igual en todas las observaciones realizadas.
Para una mejor comprensión de la heterocedasticidad, se generan algunos datos heterocedásticos bivariados, se estima un modelo de regresión lineal y luego se usan diagramas de caja para representar las distribuciones condicionales de los residuos.
# cargar el paquete de escalas para ajustar opacidades de color
library(scales)
# generar algunos datos heterocedásticos:
# establecer semillas para la reproducibilidad
set.seed(123)
# configurar vector de x coordenadas
x <- rep(c(10, 15, 20, 25), each = 25)
# inicializar vector de errores
e <- c()
# muestrear 100 errores tales que la varianza aumenta con x
e[1:25] <- rnorm(25, sd = 10)
e[26:50] <- rnorm(25, sd = 15)
e[51:75] <- rnorm(25, sd = 20)
e[76:100] <- rnorm(25, sd = 25)
# configurar y
y <- 720 - 3.3 * x + e
# estimar el modelo
mod <- lm(y ~ x)
# graficar los datos
plot(x = x,
y = y,
main = "Un ejemplo de heterocedasticidad",
xlab = "Proporción alumno-maestro",
ylab = "Resultado de la prueba",
cex = 0.5,
pch = 19,
xlim = c(8, 27),
ylim = c(600, 710))
# Agregar la línea de regresión al gráfico
abline(mod, col = "darkred")
# Agregar diagramas de caja a la trama
boxplot(formula = y ~ x,
add = TRUE,
at = c(10, 15, 20, 25),
col = alpha("gray", 0.4),
border = "black")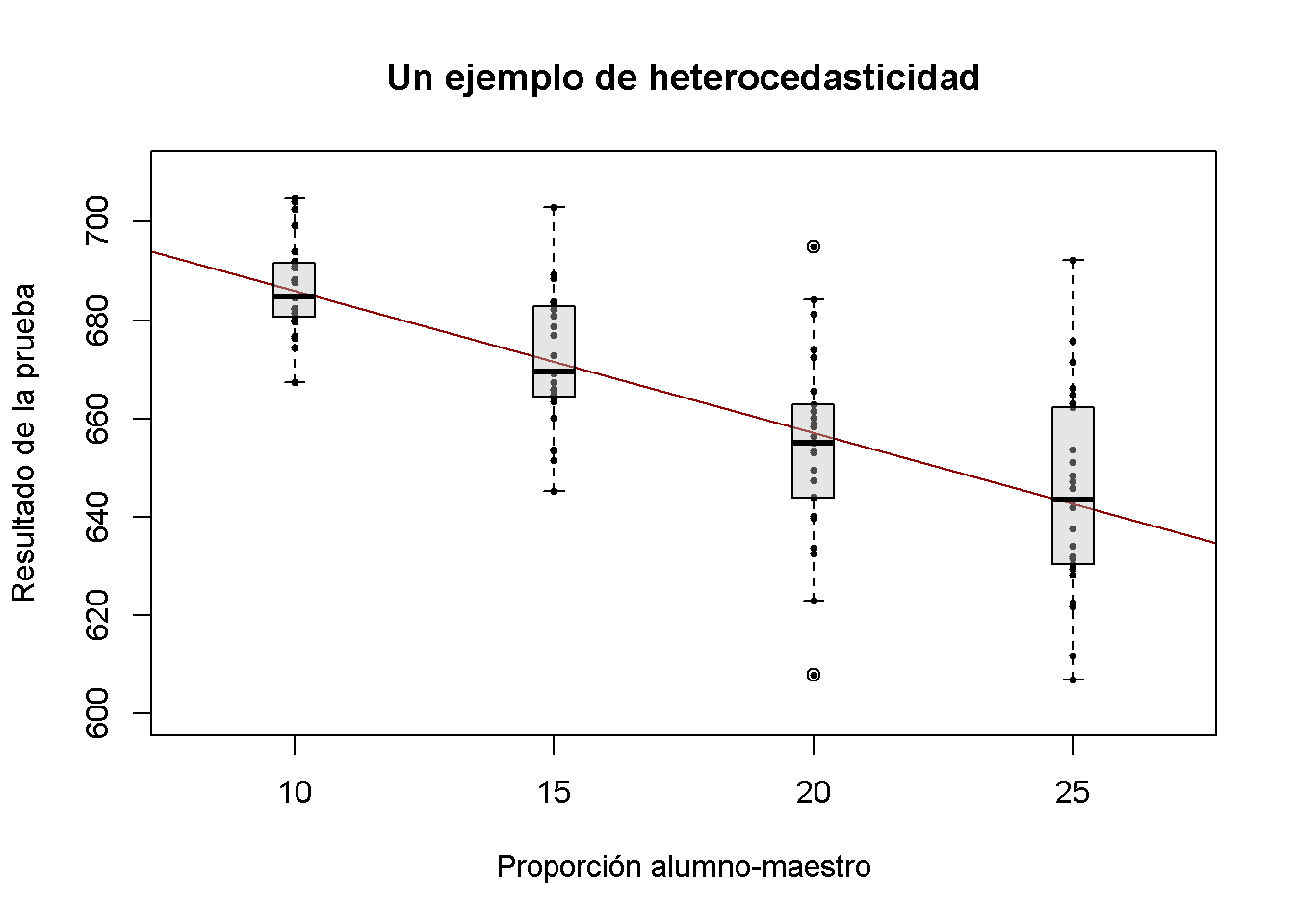
Se ha utilizado la función formula con el argumento y ~ x en boxplot() para especificar que se quiere dividir el vector y en grupos, de acuerdo con x. boxplot(y ~ x) genera un boxplot para cada uno de los grupos en y definido por X.
Para estos datos artificiales, está claro que las variaciones de error condicionales difieren. Específicamente, se observa que la varianza en los puntajes de las pruebas (y por lo tanto la varianza de los errores cometidos) aumenta con la proporción de alumnos por maestro.
Un ejemplo del mundo real de heterocedasticidad
Piense en el valor económico de la educación: Si no hubiera un valor agregado económico esperado para recibir educación universitaria, probablemente no estaría atendiendo la lectura del presente curso en este momento. Un punto de partida para verificar empíricamente tal relación es tener datos sobre las personas que trabajan. Más precisamente, se necesitan datos sobre salarios y educación de los trabajadores para estimar un modelo como
\[ wage_i = \beta_0 + \beta_1 \cdot education_i + u_i. \]
¿Qué se puede presumir de esta relación? Es probable que, en promedio, los trabajadores con mayor educación ganen más que los trabajadores con menos educación, por lo que se espera estimar una línea de regresión con pendiente ascendente. Además, parece plausible que los ingresos de los trabajadores mejor educados tengan una mayor dispersión que los de los trabajadores poco calificados: una educación sólida no es garantía para un salario alto, por lo que incluso los trabajadores altamente calificados aceptan trabajos de bajos ingresos. Sin embargo, es más probable que cumplan con los requisitos para los trabajos bien remunerados que los trabajadores con menos educación para quienes las oportunidades en el mercado laboral son mucho más limitadas.
Para verificar esto empíricamente, se pueden usar datos reales sobre ganancias por hora y el número de años de educación de los empleados. Estos datos se pueden encontrar en CPSSWEducation. Este conjunto de datos es parte del paquete AER y proviene de la Current Population Survey (CPS) que es realizada periódicamente por la Oficina de Estadísticas Laborales en los Estados Unidos.
Los siguientes fragmentos de código demuestran cómo importar los datos a R y cómo producir un gráfico:
# cargar paquete y adjuntar datos
library(AER)
data("CPSSWEducation")
attach(CPSSWEducation)
# obtener una descripción general
summary(CPSSWEducation)
#> age gender earnings education
#> Min. :29.0 female:1202 Min. : 2.137 Min. : 6.00
#> 1st Qu.:29.0 male :1748 1st Qu.:10.577 1st Qu.:12.00
#> Median :29.0 Median :14.615 Median :13.00
#> Mean :29.5 Mean :16.743 Mean :13.55
#> 3rd Qu.:30.0 3rd Qu.:20.192 3rd Qu.:16.00
#> Max. :30.0 Max. :97.500 Max. :18.00
# estimar un modelo de regresión simple
labor_model <- lm(earnings ~ education)
# graficar observaciones y agregar la línea de regresión
plot(education,
earnings,
ylim = c(0, 150))
abline(labor_model,
col = "steelblue",
lwd = 2)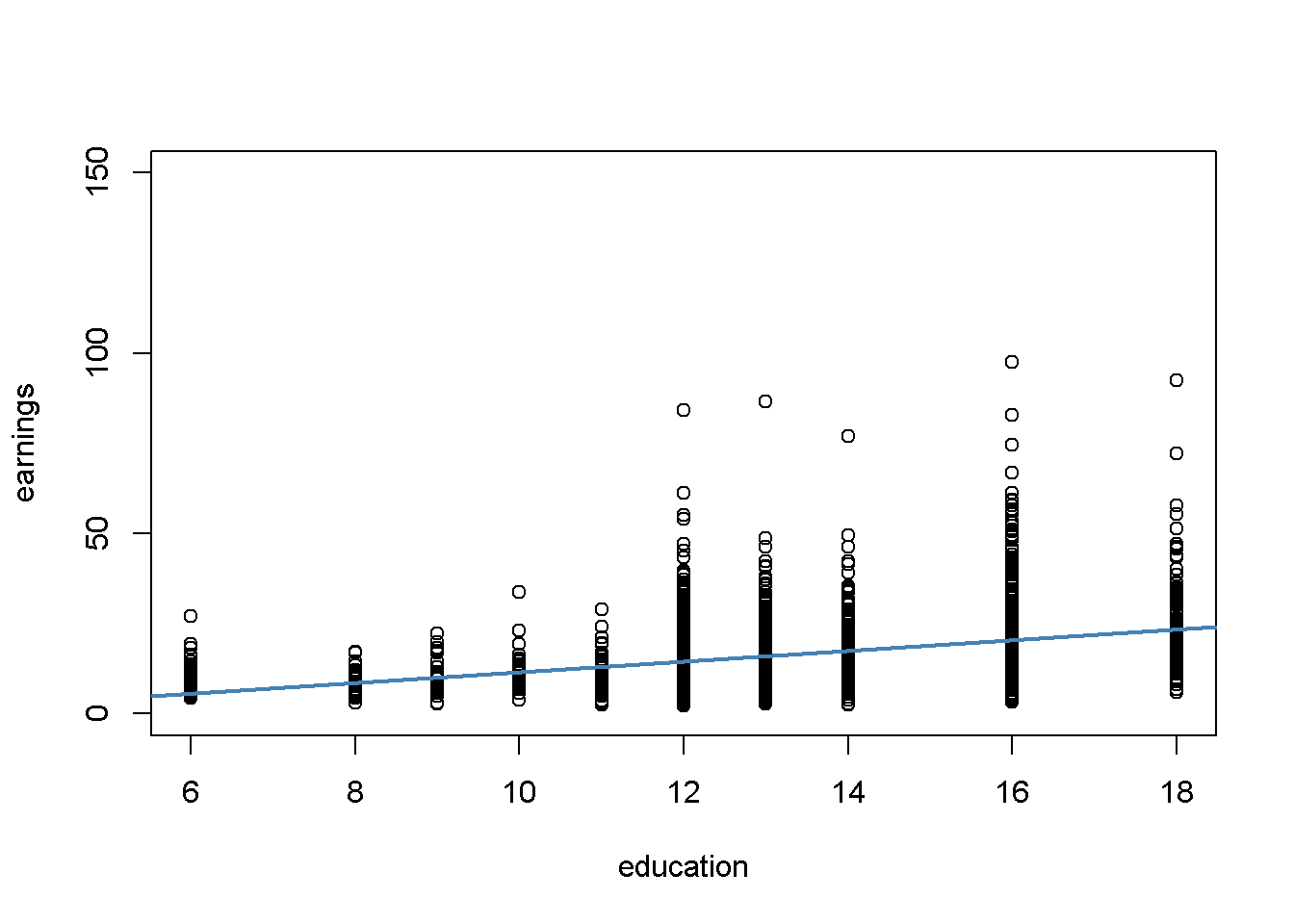
La gráfica revela que la media de la distribución de ingresos aumenta con el nivel de educación. Esto también está respaldado por un análisis formal: El modelo de regresión estimado almacenado en labor_mod muestra que existe una relación positiva entre los años de educación y los ingresos.
# imprimir el contenido de labor_model en la consola
labor_model
#>
#> Call:
#> lm(formula = earnings ~ education)
#>
#> Coefficients:
#> (Intercept) education
#> -3.134 1.467La ecuación de regresión estimada establece que, en promedio, un año adicional de educación aumenta los ingresos por hora de un trabajador en aproximadamente \(\$ 1.47\). Una vez más se usa confint() para obtener un intervalo de confianza de \(95\%\) para ambos coeficientes de regresión.
# calcular un intervalo de confianza del 95% para los coeficientes en el modelo
confint(labor_model)
#> 2.5 % 97.5 %
#> (Intercept) -5.015248 -1.253495
#> education 1.330098 1.603753Dado que el intervalo es \([1.33, 1.60]\), se puede rechazar la hipótesis de que el coeficiente de educación es cero en el nivel de \(5\%\).
Además, el gráfico indica que hay heterocedasticidad: Si se asume que la línea de regresión es una representación razonablemente buena de la función media condicional \(E(ganancias_i\vert educación_i)\), la dispersión de las ganancias por hora alrededor de esa función aumenta claramente con el nivel de la educación; es decir, aumenta la varianza de la distribución de los ingresos. En otras palabras: La varianza de los errores (los errores cometidos al explicar los ingresos por educación) aumenta con la educación, por lo que los errores de regresión son heterocedásticos.
Este ejemplo demuestra que el supuesto de homocedasticidad es dudoso en aplicaciones económicas. ¿Los economistas deberían preocuparse por la heterocedasticidad? Sí, deberían. Como se explica en la siguiente sección, la heterocedasticidad puede tener graves consecuencias negativas en la prueba de hipótesis, si se ignora.
¿Los economistas deberían preocuparse por la heterocedasticidad?
Para responder a la pregunta de si deberían preocuparse por la presencia de heterocedasticidad, se debe considerar la varianza de \(\hat\beta_1\) bajo el supuesto de homocedasticidad. En este caso se tiene:
\[ \sigma^2_{\hat\beta_1} = \frac{\sigma^2_u}{n \cdot \sigma^2_X} \tag{5.5} \]
que es una versión simplificada de la ecuación general (4.1) presentada en el Concepto clave 4.4; así como summary() estimaciones (5.5) por
\[ \overset{\sim}{\sigma}^2_{\hat\beta_1} = \frac{SER^2}{\sum_{i=1}^n (X_i - \overline{X})^2} \ \ \text{where} \ \ SER=\frac{1}{n-2} \sum_{i=1}^n \hat u_i^2. \]
Por lo tanto, summary() estima el error estándar de solo homocedasticidad:
\[\sqrt{ \overset{\sim}{\sigma}^2_{\hat\beta_1} } = \sqrt{ \frac{SER^2}{\sum_{i=1}^n(X_i - \overline{X})^2} }.\]
De hecho, este es un estimador para la desviación estándar del estimador \(\hat{\beta}_1\) que es inconsistente para el valor verdadero \(\sigma^2_{\hat\beta_1}\) cuando existe heterocedasticidad. La implicación es que el estadístico \(t\) calculado a la manera del Concepto clave 5.1 no sigue una distribución normal estándar, incluso en muestras grandes. Este problema puede invalidar la inferencia cuando se utilizan las herramientas tratadas anteriormente para la prueba de hipótesis: Se debe tener cuidado al hacer afirmaciones sobre la importancia de los coeficientes de regresión sobre la base del estadístico \(t\) calculado por summary() o intervalos de confianza producido por confint() si es dudoso que se mantenga el supuesto de homocedasticidad.
Ahora se usará R para calcular el error estándar de solo homocedasticidad para \(\hat{\beta}_1\) en el modelo de regresión de puntaje de prueba modelo_laboral a mano y se verá que coincide con el valor producido por summary().
# resumen del modelo de tienda en 'modelo'
model <- summary(labor_model)
# extraer el error estándar de la regresión del resumen del modelo
SER <- model$sigma
# calcular la variación en 'educación'
V <- (nrow(CPSSWEducation)-1) * var(education)
# calcular el error estándar del estimador del parámetro de pendiente e imprimirlo
SE.beta_1.hat <- sqrt(SER^2/V)
SE.beta_1.hat
#> [1] 0.06978281
# utilizar los operadores lógicos para ver si el valor calculado coincide con el proporcionado
# en mod$coefficients, redondear estimaciones a cuatro lugares decimales
round(model$coefficients[2, 2], 4) == round(SE.beta_1.hat, 4)
#> [1] TRUEDe hecho, los valores estimados son iguales.
Cálculo de errores estándar robustos de heterocedasticidad
Se otorga una estimación consistente de \(\sigma_{\hat{\beta}_1}\) bajo heterocedasticidad cuando se usa el siguiente estimador robusto:
\(SE(\hat{\beta}_1) = \sqrt{ \frac{1}{n} \cdot \frac{ \frac{1}{n} \sum_{i=1}^n (X_i - \overline{X})^2 \hat{u}_i^2 }{ \left[ \frac{1}{n} \sum_{i=1}^n (X_i - \overline{X})^2 \right]^2} } \tag{5.6}\)
Las estimaciones de error estándar calculadas de esta manera también se conocen como errores estándar de Eicker-Huber-White, el artículo más frecuentemente citado sobre esto es White (1980).
Puede resultar bastante engorroso hacer este cálculo a mano. Afortunadamente, existen ciertas funciones en R que cumplen con ese propósito. Uno conveniente llamado vcovHC() es parte del paquete sandwich.1 Dicha función puede calcular una variedad de errores estándar. El presentado en (5.6) se calcula cuando el argumento type se establece en “HC0”. La mayoría de los ejemplos presentados en los libros de texto encuentran fundamento en una fórmula ligeramente diferente, que es la predeterminada en el paquete de estadísticas STATA:
\[\begin{align} SE(\hat{\beta}_1)_{HC1} = \sqrt{ \frac{1}{n} \cdot \frac{ \frac{1}{n-2} \sum_{i=1}^n (X_i - \overline{X})^2 \hat{u}_i^2 }{ \left[ \frac{1}{n} \sum_{i=1}^n (X_i - \overline{X})^2 \right]^2}} \tag{6.2} \end{align}\]
La diferencia es que se multiplica por \(\frac{1}{n-2}\) en el numerador de (6.2). Esta es una corrección de grados de libertad y fue considerada por MacKinnon and White (1985). Para que vcovHC() use (6.2), se tiene que establecer type = “HC1”.
Calcular ahora estimaciones robustas del error estándar para los coeficientes en modelo_lineal.
# calcular errores estándar robustos a la heterocedasticidad
vcov <- vcovHC(linear_model, type = "HC1")
vcov
#> (Intercept) STR
#> (Intercept) 107.419993 -5.3639114
#> STR -5.363911 0.2698692La salida de vcovHC() es la matriz de varianza-covarianza de estimaciones de coeficientes. Se está interesado en la raíz cuadrada de los elementos diagonales de esta matriz; es decir, las estimaciones del error estándar.
Cuando se tiene k > 1 regresores, escribir las ecuaciones para un modelo de regresión se vuelve muy complicado. Una forma más conveniente de denotar y estimar los llamados modelos de regresión múltiple (ver Capítulo 7) es usando álgebra matricial. Es por eso que funciones como vcovHC() producen matrices. En el modelo de regresión lineal simple, las varianzas y covarianzas de los estimadores se pueden recopilar en la matriz simétrica de varianza-covarianza.
\[\begin{equation} \text{Var} \begin{pmatrix} \hat\beta_0 \\ \hat\beta_1 \end{pmatrix} = \begin{pmatrix} \text{Var}(\hat\beta_0) & \text{Cov}(\hat\beta_0,\hat\beta_1) \\ \text{Cov}(\hat\beta_0,\hat\beta_1) & \text{Var}(\hat\beta_1) \end{pmatrix}, \end{equation}\]
entonces vcovHC() da \(\widehat{\text{Var}}(\hat\beta_0)\), \(\widehat{\text{Var}}(\hat\beta_1)\) y \(\widehat{\text{Cov}}(\hat\beta_0,\hat\beta_1)\), pero la mayoría de las veces se está interesado en los elementos diagonales de la matriz estimada.
# calcular la raíz cuadrada de los elementos diagonales en vcov
robust_se <- sqrt(diag(vcov))
robust_se
#> (Intercept) STR
#> 10.3643617 0.5194893Ahora suponga que se quiere generar un resumen de coeficientes como lo proporciona summary(), pero con errores estándar robustos de los estimadores de coeficientes, estadísticos robustas de \(t\) y valores de \(p\) correspondientes para el modelo de regresión linear_model. Esto se puede hacer usando coeftest() del paquete lmtest, ver ?coeftest. Más adelante se especifica en el argumento vcov. que debe usarse vcov, la estimación de Eicker-Huber-White de la matriz de varianza que se ha calculado antes.
# se invoca la función `coeftest()` en el modelo
coeftest(linear_model, vcov. = vcov)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 698.93295 10.36436 67.4362 < 2.2e-16 ***
#> STR -2.27981 0.51949 -4.3886 1.447e-05 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Se puede ver que los valores reportados en la columna Std. Error son iguales a los de sqrt(diag(vcov)).
¿Qué tan severas son las implicaciones de usar errores estándar de solo homocedasticidad en presencia de heterocedasticidad? La respuesta es, depende. Como se mencionó anteriormente, se corre el riesgo de sacar conclusiones erróneas al realizar pruebas de significancia.
Resulta importante ilustrar este punto generando otro ejemplo de un conjunto de datos heterocedásticos, usándolo para estimar un modelo de regresión simple. En este caso se toma:
\[ Y_i = \beta_1 \cdot X_i + u_i \ \ , \ \ u_i \overset{i.i.d.}{\sim} \mathcal{N}(0,0.36 \cdot X_i^2) \]
con \(\beta_1=1\) como proceso de generación de datos. Claramente, aquí se viola el supuesto de homocedasticidad, dado que la varianza de los errores es una función creciente no lineal de \(X_i\), pero los errores tienen media cero y son i.i.d. de manera que no se violen las suposiciones hechas en el Concepto clave 4.3. Como antes, se está interesado en estimar \(\beta_1\).
set.seed(905)
# generar datos heterocedásticos
X <- 1:500
Y <- rnorm(n = 500, mean = X, sd = 0.6 * X)
# estimar un modelo de regresión simple
reg <- lm(Y ~ X)Se grafican los datos y se agrega la línea de regresión.
# graficar los datos
plot(x = X, y = Y,
pch = 19,
col = "steelblue",
cex = 0.8)
# agregar la línea de regresión al gráfico
abline(reg,
col = "darkred",
lwd = 1.5)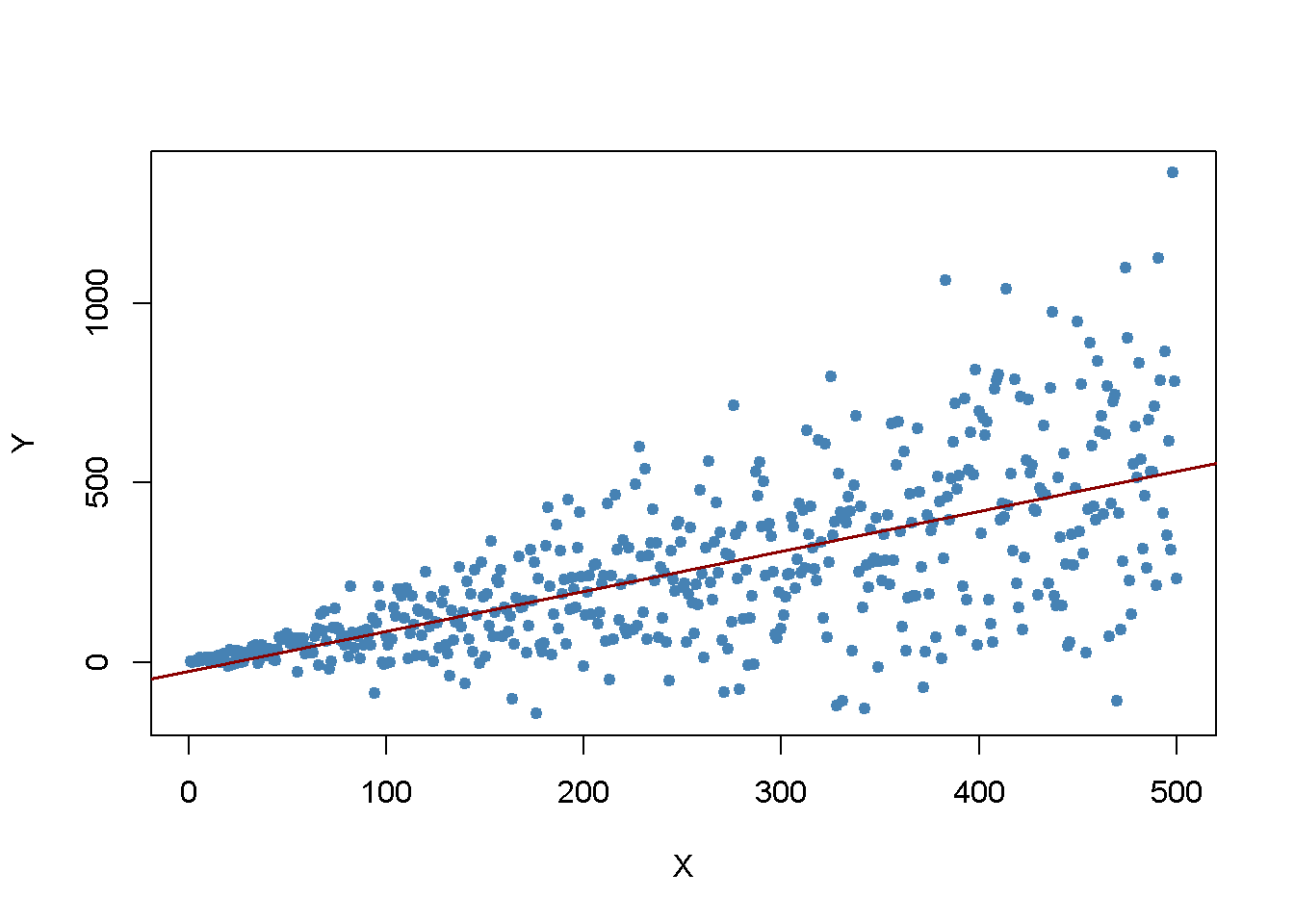
La gráfica muestra que los datos son heterocedásticos a medida que la varianza de \(Y\) crece con \(X\). A continuación, se realiza una prueba de significancia de la hipótesis nula (verdadera) \(H_0: \beta_1 = 1\) dos veces, una vez usando la fórmula de error estándar de homocedasticidad solamente y una vez con la versión robusta (5.6). Una manera fácil de hacer esto en R es la función linearHypothesis() del paquete car, ver ?LinearHypothesis. Permite probar hipótesis lineales sobre parámetros en modelos lineales de manera similar a como se hace con un estadístico \(t\) y ofrecer varios estimadores de matrices de covarianza robustas. Se prueba comparando los valores \(p\) de las pruebas con el nivel de significancia de \(5\%\).
linearHypothesis() calcula una estadística de prueba que sigue una distribución \(F\) bajo la hipótesis nula. No es momento de centrarse en los detalles de la teoría subyacente. En general, la idea de la prueba \(F\) es comparar el ajuste de diferentes modelos. Cuando se prueba una hipótesis sobre un coeficiente único usando una prueba \(F\), se puede mostrar que la estadística de prueba es simplemente el cuadrado del estadístico \(t\) correspondiente:
\[ F = t ^ 2 = \ left (\ frac {\ hat \ beta_i - \ beta_ {i, 0}} {SE (\ hat \ beta_i)} \ right) ^ 2 \ sim F_ {1, nk-1 } \]
En linearHypothesis(), existen diferentes formas de especificar la hipótesis que se va a probar; por ejemplo, utilizando un vector del tipo character (como se hace en el siguiente fragmento de código), ver ?linearHypothesis para alternativas. La función devuelve un objeto de clase anova que contiene más información sobre la prueba a la que se puede acceder utilizando el operador $.# probar la hipótesis utilizando la fórmula de error estándar predeterminada
linearHypothesis(reg, hypothesis.matrix = "X = 1")$'Pr(>F)'[2] < 0.05
#> [1] TRUE
# probar hipótesis usando la fórmula robusta de error estándar
linearHypothesis(reg, hypothesis.matrix = "X = 1", white.adjust = "hc1")$'Pr(>F)'[2] < 0.05
#> [1] FALSEEste es un buen ejemplo de lo que puede salir mal si se ignora la heterocedasticidad: Para el conjunto de datos en cuestión, el método predeterminado rechaza la hipótesis nula \(\beta_1 = 1\) aunque es cierta. Cuando se utiliza la fórmula robusta de error estándar, la prueba no rechaza la hipótesis nula. Por supuesto, se podría pensar que esto es solo una coincidencia y ambas pruebas funcionan igualmente bien para mantener la tasa de error de tipo I de \(5\%\). Esto se puede investigar más a fondo calculando estimaciones de Monte Carlo de las frecuencias de rechazo de ambas pruebas sobre la base de un gran número de muestras aleatorias. Se procede de la siguiente manera:
- Inicializar los vectores t y t.rob.
- Usar un bucle for() para generar \(10000\) muestras aleatorias heterocedásticas de tamaño \(1000\), se estima el modelo de regresión y se verifica si las pruebas rechazan falsamente la hipótesis nula al nivel de \(5\%\) usando operadores de comparación. Los resultados se almacenan en los vectores respectivos t y t.rob.
- Después de la simulación, se calcula la fracción de falsos rechazos para ambas pruebas.
# inicializar los vectores t y t.rob
t <- c()
t.rob <- c()
# muestreo y estimación de bucles
for (i in 1:10000) {
# datos de muestra
X <- 1:1000
Y <- rnorm(n = 1000, mean = X, sd = 0.6 * X)
# estimar modelo de regresión
reg <- lm(Y ~ X)
# prueba de significación solo de homocedasticidad
t[i] <- linearHypothesis(reg, "X = 1")$'Pr(>F)'[2] < 0.05
# prueba de significancia robusta
t.rob[i] <- linearHypothesis(reg, "X = 1", white.adjust = "hc1")$'Pr(>F)'[2] < 0.05
}
# calcular la fracción de falsos rechazos
round(cbind(t = mean(t), t.rob = mean(t.rob)), 3)
#> t t.rob
#> [1,] 0.073 0.05Estos resultados revelan un mayor riesgo de rechazar falsamente la hipótesis nula utilizando el error estándar de solo homocedasticidad para el problema de prueba en cuestión: Con el error estándar común, \(7.28\%\) de todas las pruebas rechazan falsamente la hipótesis nula. Por el contrario, con la estadística de prueba robusta se esta más cerca del nivel nominal de \(5\%\).
Referencias bibliográficas
El paquete sandwich es una dependencia del paquete AER, lo que implica que se adjunta automáticamente si se carga AER.↩︎