4.2 Propiedades de la media muestral
Una forma más precisa de expresar la consistencia de un estimador \(\hat\mu\) para un parámetro \(\mu\) es
\[ P(|\hat{\mu} - \mu|<\epsilon) \xrightarrow[n \rightarrow \infty]{p} 1 \quad \text{for any}\quad\epsilon>0.\]
Esta expresión implica que la probabilidad de observar una desviación del valor verdadero de \(\mu\) que es menor que algún \(\epsilon > 0\) arbitrario converge a \(1\) a medida que \(n\) crece. La consistencia no requiere imparcialidad.Para examinar las propiedades de la media muestral como estimador de la media poblacional correspondiente, considere el siguiente ejemplo en R.
Se genera una población pop que consta de observaciones \(Y_i\), \(i=1,\dots,10000\) que se originan en una distribución normal con media \(\mu = 10\) y varianza \(\sigma^2 = 1\).
Para investigar el comportamiento del estimador \(\hat{\mu} = \bar{Y}\) se pueden extraer muestras aleatorias de esta población y calcular \(\bar{Y}\) para cada una de ellas. Esto se hace fácilmente haciendo uso de la función replicate(). El argumento expr se evalúa n veces. En este caso, se extraen muestras de tamaños \(n = 5\) y \(n = 25\), se calculan las medias muestrales y se repite esto exactamente \(N = 25000\) veces.
Para fines de comparación, se almacenan los resultados para el estimador \(Y_1\), la primera observación en una muestra para una muestra de tamaño \(5\), por separado.
# generar una población ficticia
pop <- rnorm(10000, 10, 1)
# muestra de la población y estimación de la media
est1 <- replicate(expr = mean(sample(x = pop, size = 5)), n = 25000)
est2 <- replicate(expr = mean(sample(x = pop, size = 25)), n = 25000)
fo <- replicate(expr = sample(x = pop, size = 5)[1], n = 25000)Comprobar que est1 y est2 son vectores de longitud \(25000\):
# comprobar si el tipo de objeto es vector
is.vector(est1)
#> [1] TRUE
is.vector(est2)
#> [1] TRUE
# comprobar la longitud
length(est1)
#> [1] 25000
length(est2)
#> [1] 25000El fragmento de código a continuación produce una gráfica de las distribuciones muestrales de los estimadores \(\bar{Y}\) y \(Y_1\) sobre la base de las muestras de \(25000\) en cada caso. También se grafica la función de densidad de la distribución \(\mathcal{N}(10,1)\).
# graficar la densidad de la estimación Y_1
plot(density(fo),
col = "green",
lwd = 2,
ylim = c(0, 2),
xlab = "Estimados",
main = "Distribuciones muestrales de estimadores insesgados")
# agregar la estimación de densidad para la distribución de la media muestral con n = 5 a la gráfica
lines(density(est1),
col = "steelblue",
lwd = 2,
bty = "l")
# agregar la estimación de densidad para la distribución de la media muestral con n = 25 a la gráfica
lines(density(est2),
col = "red2",
lwd = 2)
# agregar una línea vertical en el parámetro verdadero
abline(v = 10, lty = 2)
# agregar la densidad N(10, 1) a la gráfica
curve(dnorm(x, mean = 10),
lwd = 2,
lty = 2,
add = T)
# agregar una leyenda
legend("topleft",
legend = c("N(10,1)",
expression(Y[1]),
expression(bar(Y) ~ n == 5),
expression(bar(Y) ~ n == 25)
),
lty = c(2, 1, 1, 1),
col = c("black","green", "steelblue", "red2"),
lwd = 2)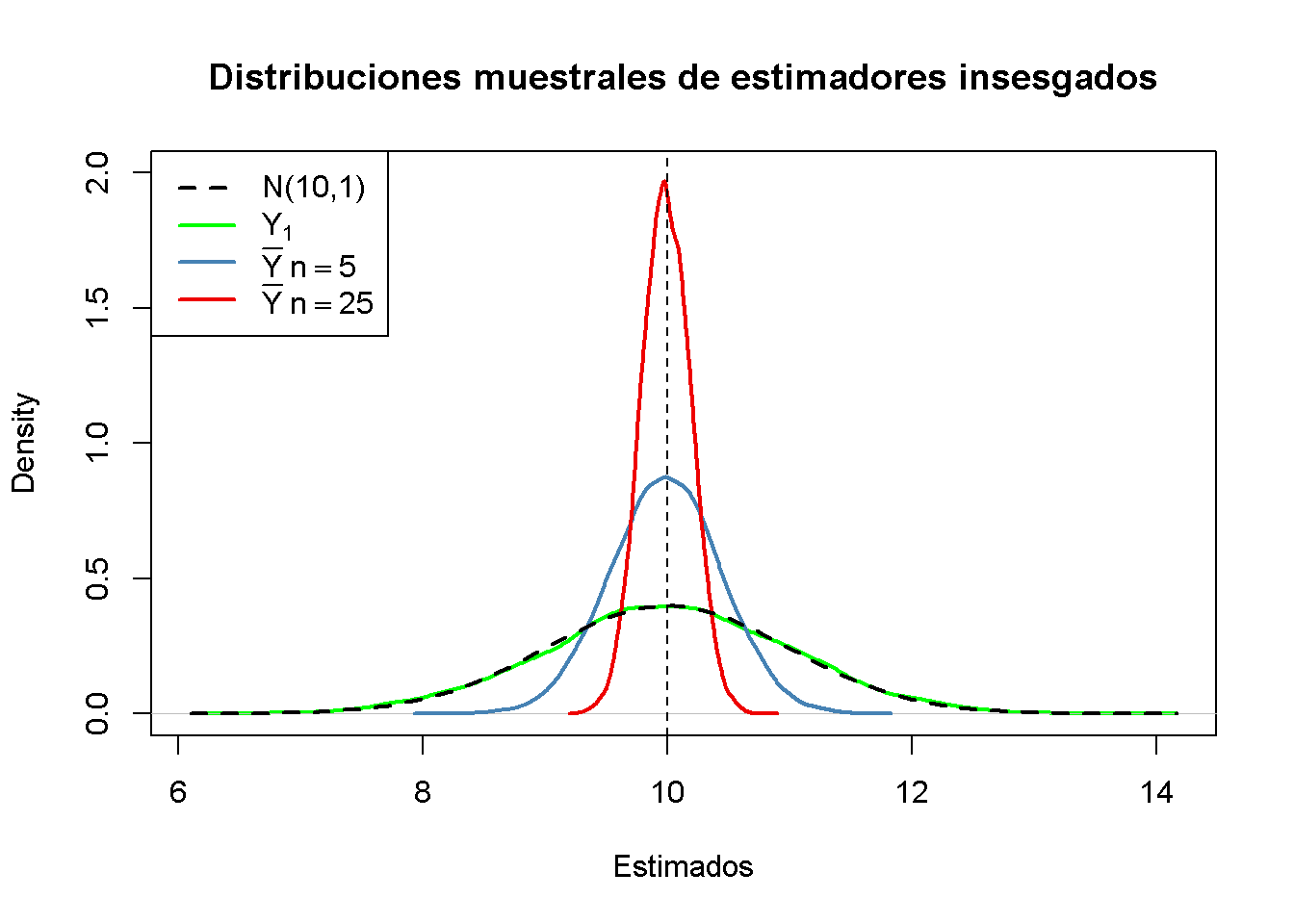
Primero, todas las distribuciones de muestreo (representadas por líneas continuas) se centran alrededor de \(\mu = 10\). Esto es evidencia de la imparcialidad de \(Y_1\), \(\overline{Y}_{5}\) y \(\overline{Y}_{25}\). Por supuesto, la densidad teórica \(\mathcal{N}(10,1)\) también se centra en \(10\).
A continuación, se observa la extensión de las distribuciones muestrales. Varias cosas son dignas de mención:
La distribución de muestreo de \(Y_1\) (curva verde) rastrea la densidad de la distribución \(\mathcal{N}(10,1)\) (línea discontinua negra) bastante de cerca. De hecho, la distribución muestral de \(Y_1\) es la distribución \(\mathcal{N}(10,1)\). Esto es menos sorprendente si se tiene en cuenta que el estimador \(Y_1\) no hace más que informar una observación que se selecciona al azar de una población con distribución \(\mathcal{N}(10,1)\). Por lo tanto, \(Y_1 \sim \mathcal{N}(10,1)\). Se debe tener en cuenta que este resultado no depende del tamaño de la muestra \(n\): la distribución muestral de \(Y_1\) es siempre la distribución de la población, sin importar el tamaño de la muestra. \(Y_1\) es una buena estimación de \(\mu_Y\), pero se puede hacer mejor.
Ambas distribuciones de muestreo de \(\overline{Y}\) muestran menos dispersión que la distribución de muestreo de \(Y_1\). Lo cual implica que \(\overline{Y}\) tiene una variación menor que \(Y_1\). En vista de los Conceptos clave 3.2 y 3.3, se encuentra que \(\overline{Y}\) es un estimador más eficiente que \(Y_1\). De hecho, esto es válido para todos los \(n > 1\).
\(\overline{Y}\) muestra un comportamiento que ilustra la coherencia (ver Concepto clave 3.2). Las densidades azul y roja están mucho más concentradas alrededor de \(\mu=10\) que la verde. A medida que aumenta el número de observaciones de \(1\) a \(5\), la distribución muestral se ajusta en torno al parámetro verdadero. Al aumentar el tamaño de la muestra a \(25\), este efecto se vuelve más evidente. Esto implica que la probabilidad de obtener estimaciones cercanas al valor real aumenta con \(n\). Esto también se refleja en los valores estimados de la función de densidad cercanos a \(10\): cuanto mayor es el tamaño de la muestra, mayor es el valor de la densidad.
Se recomienda que siga adelante y modifique el código. Pruebe diferentes valores para el tamaño de la muestra y vea cómo cambia la distribución muestral de \(\overline{Y}\).
\(\overline{Y}\) es el estimador de mínimos cuadrados de \(\mu_Y\)
Suponga que tiene algunas observaciones \(Y_1,\dots,Y_n\) en \(Y \sim \mathcal{N}(10,1)\) (que se desconoce) y le gustaría encontrar un estimador \(m\) que prediga las observaciones también como sea posible. Por bueno se quiere decir elegir \(m\) de manera que la desviación al cuadrado total entre el valor predicho y los valores observados sea pequeña. Matemáticamente, esto significa que se quiere encontrar un \(m\) que minimice
\[\begin{equation} \sum_{i=1}^n (Y_i - m)^2. \tag{4.1} \end{equation}\]
Piense en \(Y_i - m\) como el error cometido al predecir \(Y_i\) por \(m\). También se podría minimizar la suma de las desviaciones absolutas de \(m\), pero minimizar la suma de las desviaciones al cuadrado es matemáticamente más conveniente (y conduce a un resultado diferente). Es por eso que el estimador que se está buscando se llama estimador de mínimos cuadrados. \(m = \overline{Y}\), la media de la muestra, es este estimador.
Se puede mostrar esto generando una muestra aleatoria y graficando (4.1) como una función de \(m\).
# definir la función y vectorizarla
sqm <- function(m) {
sum((y-m)^2)
}
sqm <- Vectorize(sqm)
# extraer una muestra aleatoria y calcular la media
y <- rnorm(100, 10, 1)
mean(y)
#> [1] 10.1364# graficar la función objetivo
curve(sqm(x),
from = -50,
to = 70,
xlab = "m",
ylab = "sqm(m)")
# agregar una línea vertical en la media (y)
abline(v = mean(y),
lty = 2,
col = "darkred")
# agregar anotación en la media (y)
text(x = mean(y),
y = 0,
labels = paste(round(mean(y), 2)))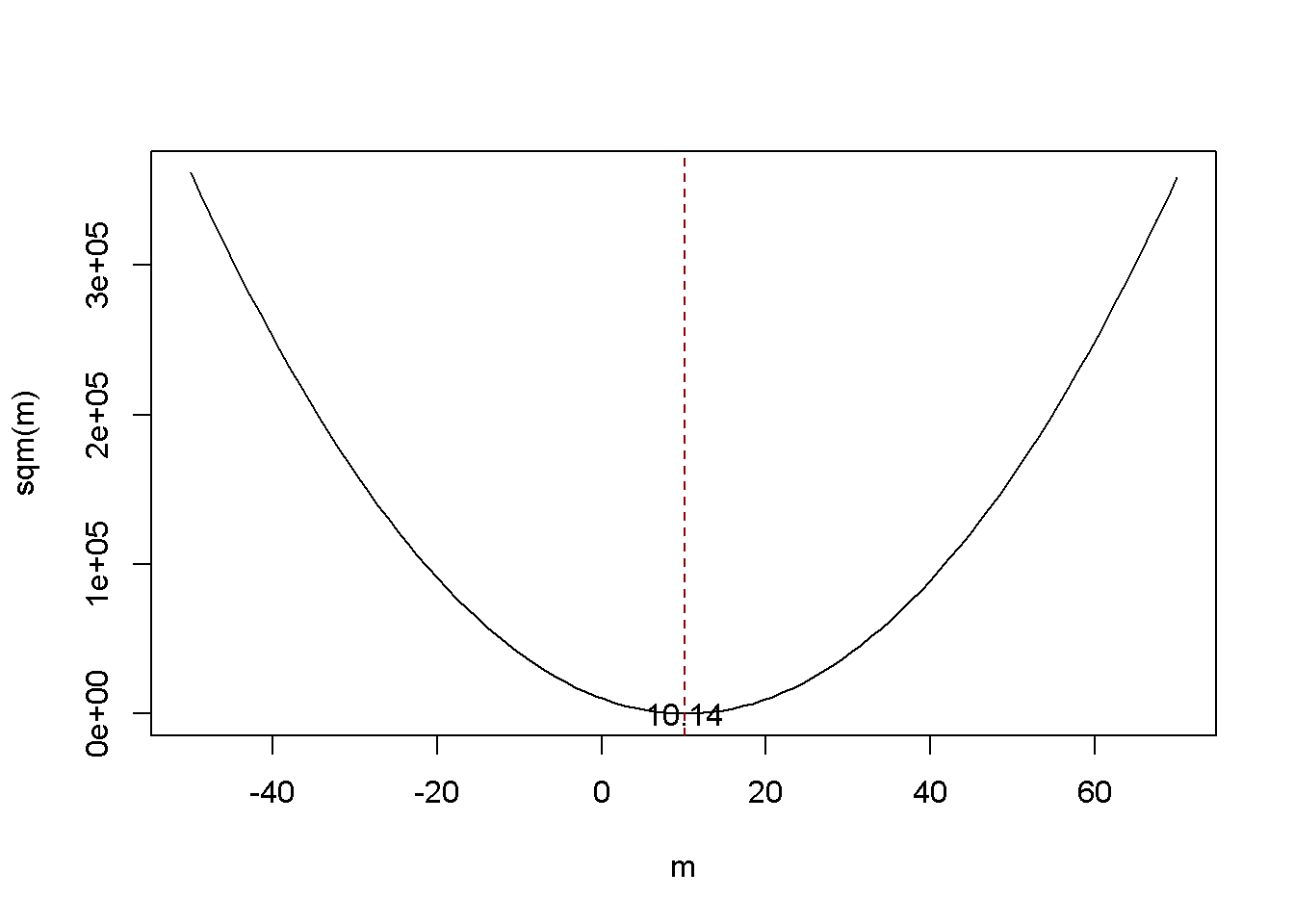
Observe que (4.1) es una función cuadrática, por lo que solo hay un mínimo. La gráfica muestra que este mínimo se encuentra exactamente en la media muestral de los datos muestrales.
Algunas funciones en R solo pueden interactuar con funciones que toman un vector como entrada y evalúan el cuerpo de la función en cada entrada del vector, por ejemplo curve(). A estas funciones se les da el nombre de funciones vectorizadas y, a menudo, es una buena idea escribir las funciones vectorizadas por usted mismo, aunque esto es engorroso en algunos casos. Tener una función vectorizada en R nunca es un inconveniente ya que estas funciones sirven tanto para valores únicos, así como para vectores.
Se puede ver la función sqm(), que no está vectorizada:
sqm <- function(m) {
sum((y-m)^2) #cuerpo de la función
}
Proporcionar, por ejemplo, c (1,2,3) como argumento m causaría un error, ya que entonces la operación ym no es válida: los vectores y y m son de dimensiones incompatibles. Es por eso que no se puede usar sqm() junto con curve().
Aquí entra en juego Vectorize(). Genera una versión vectorizada de una función no vectorizada.¿Por qué es importante el muestreo aleatorio?
Hasta ahora, se asume (a veces implícitamente) que los datos observados \(Y_1, \dots, Y_n\) son el resultado de un proceso de muestreo que satisface el supuesto de muestreo aleatorio simple. Esta suposición a menudo se cumple al estimar la media de una población usando \(\overline{Y}\). Si este no es el caso, las estimaciones pueden estar sesgadas.
Volviendo a pop, la población ficticia de observaciones de \(10000\) y calcular la media de la población \(\mu_{\texttt{pop}}\):
# calcular la media poblacional de pop
mean(pop)
#> [1] 9.992604A continuación, se toman muestras de \(10\) observaciones de pop con sample() y se estima \(\mu_{\texttt{pop}}\) usando \(\overline{Y}\) repetidamente. Sin embargo, ahora se usa un esquema de muestreo que se desvía del muestreo aleatorio simple: en lugar de asegurar que cada miembro de la población tenga la misma probabilidad de terminar en una muestra, se asigna una probabilidad más alta de ser muestreada a las observaciones más pequeñas de \(2500\) de la población estableciendo el argumento prob en un vector adecuado de ponderaciones de probabilidad:
# simular resultados para la media muestral cuando la suposición de variables aleatorias i.i.d. falla
est3 <- replicate(n = 25000,
expr = mean(sample(x = sort(pop),
size = 10,
prob = c(rep(4, 2500), rep(1, 7500)))))
# calcular la media muestral de los resultados
mean(est3)
#> [1] 9.444113A continuación, se traza la distribución muestral de \(\overline{Y}\) para el caso de no i.i.d. y se compara con la distribución muestral cuando la suposición de i.i.d. se mantiene.
# distribución muestral de la media muestral, i.i.d. sostiene, n = 25
plot(density(est2),
col = "steelblue",
lwd = 2,
xlim = c(8, 11),
xlab = "Estimados",
main = "Cuando la suposición de i.i.d. falla")
# distribución muestral de la media muestral, i.i.d. falla, n = 25
lines(density(est3),
col = "red2",
lwd = 2)
# agrega una leyenda
legend("topleft",
legend = c(expression(bar(Y)[n == 25]~", i.i.d. falla"),
expression(bar(Y)[n == 25]~", i.i.d. se mantiene")
),
lty = c(1, 1),
col = c("red2", "steelblue"),
lwd = 2)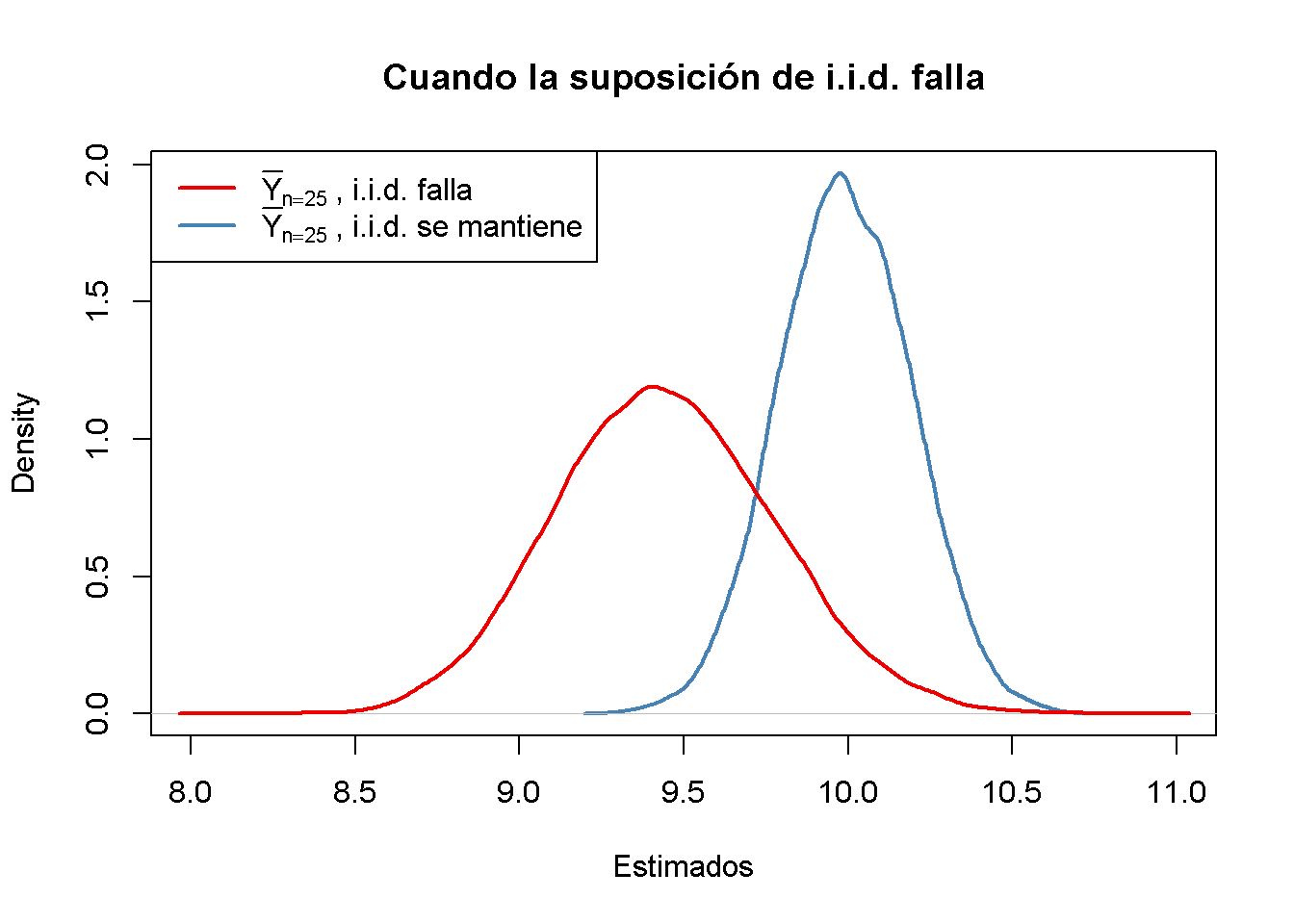
Aquí, el fracaso de la suposición de i.i.d. implica que, en promedio, se ha subestimado \(\mu_Y\) usando \(\overline{Y}\): la distribución correspondiente de \(\overline{Y}\) se desplaza hacia la izquierda. En otras palabras, \(\overline{Y}\) es un estimador sesgado para \(\mu_Y\) si la suposición de i.i.d. no se sostiene.