5.4 Supuestos de mínimos cuadrados
MCO funciona bien en una amplia variedad de circunstancias diferentes. Sin embargo, existen algunas suposiciones que deben cumplirse para asegurar que las estimaciones se distribuyan normalmente en muestras grandes (se discute esto en el Capítulo 5.5.
Concepto clave 4.3
Los supuestos de mínimos cuadrados
\[Y_i = \beta_0 + \beta_1 X_i + u_i \text{, } i = 1,\dots,n\]
donde
- El término de error \(u_i\) tiene una media condicional cero dada \(X_i\): \(E(u_i|X_i) = 0\).
- \((X_i,Y_i), i = 1,\dots,n\) son extractos independientes e idénticamente distribuidos (i.i.d.) de su distribución conjunta.
- Los valores atípicos grandes son poco probables: \(X_i\) y \(Y_i\) tienen momentos finitos distintos de cero.
Supuesto 1: El término de error tiene una media condicional de cero
Esto significa que, independientemente del valor que se elija para \(X\), el término de error \(u\) no debe mostrar ningún patrón sistemático y debe tener una media de \(0\). Considere el caso de que, incondicionalmente, \(E(u) = 0\), pero para valores bajos y altos de \(X\), el término de error tiende a ser positivo y para valores de rango medio de \(X\) el error tiende a ser negativo. Se puede usar R para construir tal ejemplo. Para hacerlo, se generan datos propios utilizando los generadores de números aleatorios integrados de R.
Se usarán las siguientes funciones:
- runif() - genera números aleatorios distribuidos uniformemente
- rnorm() - genera números aleatorios distribuidos normalmente
- predecir() - realiza predicciones basadas en los resultados de funciones de ajuste del modelo como lm()
- lines() - agrega segmentos de línea a un gráfico existente
Se comienza creando un vector que contenga valores que se distribuyan uniformemente en el intervalo \([-5, 5]\). Esto se puede hacer con la función runif(). También se necesita simular el término de error. Para esto, se generan números aleatorios normalmente distribuidos con una media igual a \(0\) y una varianza de \(1\) usando rnorm(). Los valores de \(Y\) se obtienen como una función cuadrática de los valores de \(X\) y del error.
Después de generar los datos, se estima tanto un modelo de regresión simple como un modelo cuadrático que también incluye el regresor \(X^2\) (este es un modelo de regresión múltiple, consulte el Capítulo 7). Finalmente, se grafican los datos simulados y se agrega la línea de regresión estimada de un modelo de regresión simple, así como las predicciones hechas con un modelo cuadrático para comparar el ajuste gráficamente.
# establecer una semilla para que los resultados sean reproducibles
set.seed(321)
# simular los datos
X <- runif(50, min = -5, max = 5)
u <- rnorm(50, sd = 1)
# la verdadera relación
Y <- X^2 + 2 * X + u
# estimar un modelo de regresión simple
mod_simple <- lm(Y ~ X)
# predecir usando un modelo cuadrático
prediction <- predict(lm(Y ~ X + I(X^2)), data.frame(X = sort(X)))
# graficar los resultados
plot(Y ~ X)
abline(mod_simple, col = "red")
lines(sort(X), prediction)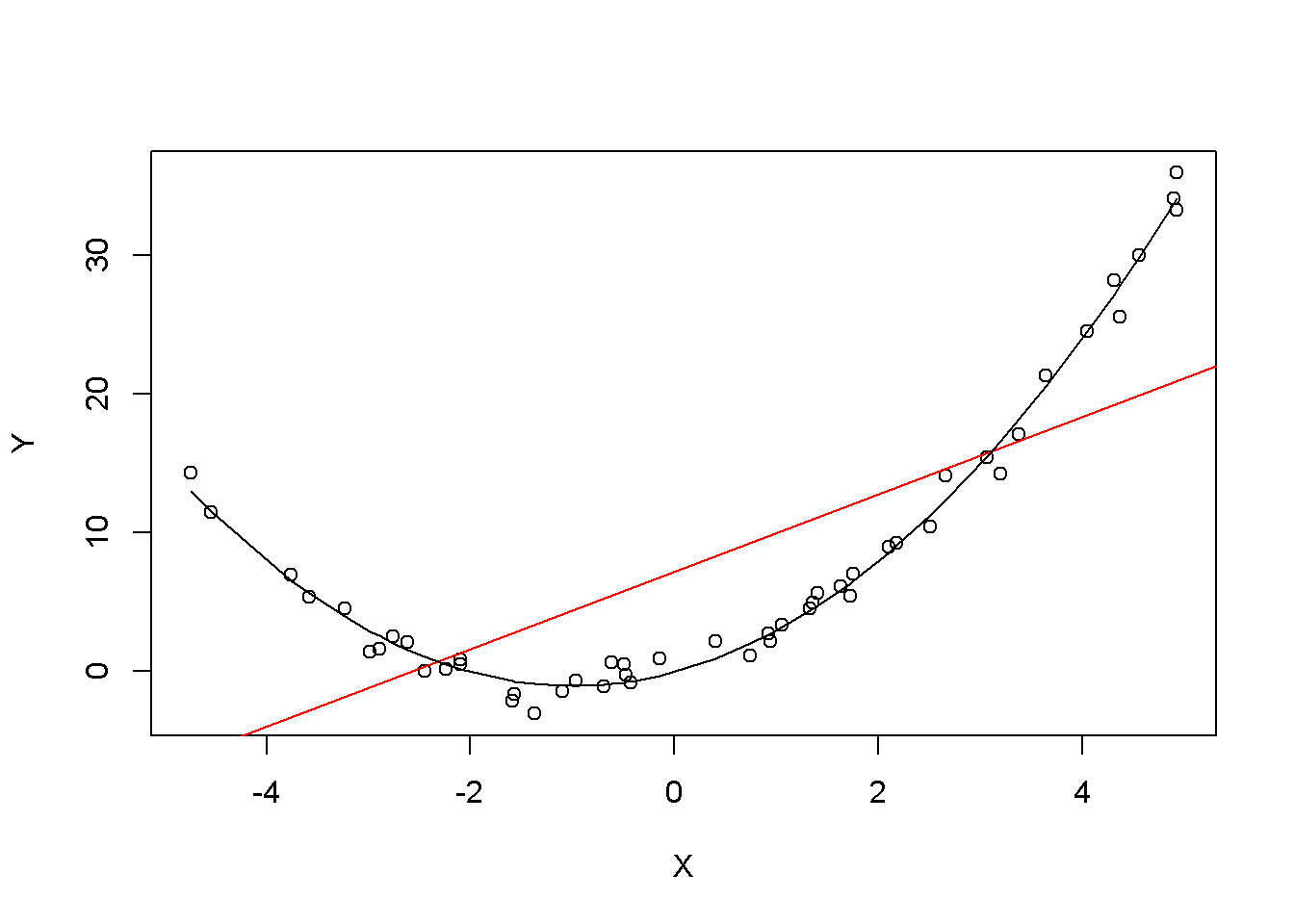
El gráfico muestra qué se entiende por \(E(u_i|X_i) = 0\) y por qué no es válido para el modelo lineal:
Usando el modelo cuadrático (representado por la curva negra) se ve que no existe desviaciones sistemáticas de la observación de la relación predicha. Es creíble que no se viole la suposición cuando se emplea tal modelo. Sin embargo, al usar un modelo de regresión lineal simple, se ve que la suposición probablemente se viola ya que \(E(u_i|X_i)\) varía con \(X_i\).
Supuesto 2: Datos independientes e idénticamente distribuidos
La mayoría de los esquemas de muestreo utilizados para recopilar datos de poblaciones producen muestras i.i.d. Por ejemplo, se podría usar el generador de números aleatorios de R para seleccionar al azar las identificaciones de los estudiantes de la lista de inscripción de una universidad y registrar la edad \(X\) y los ingresos \(Y\) de los estudiantes correspondientes. Este es un ejemplo típico de muestreo aleatorio simple y garantiza que todos los \((X_i, Y_i)\) se extraigan al azar de la misma población.
Un ejemplo destacado en que la suposición de i.i.d. no se cumple es en los datos de series de tiempo donde se tienen observaciones en la misma unidad a lo largo del tiempo. Por ejemplo, al tomar \(X\) como el número de trabajadores en una empresa de producción a lo largo del tiempo. Debido a las transformaciones comerciales, la empresa recorta puestos de trabajo periódicamente por una participación específica, pero también hay algunas influencias no deterministas que se relacionan con la economía, la política, entre otrs. Con R se puede simular fácilmente un proceso de este tipo y graficarlo.
Se comienza la serie con un total de 5000 trabajadores y se simula la reducción del empleo con un proceso autorregresivo que exhibe un movimiento descendente en el largo plazo y tiene errores normalmente distribuidos:1
\[ employment_t = -5 + 0.98 \cdot employment_{t-1} + u_t \]
# sembrar semilla
set.seed(123)
# generar un vector de fecha
Date <- seq(as.Date("1951/1/1"), as.Date("2000/1/1"), "years")
# inicializar el vector de empleo
X <- c(5000, rep(NA, length(Date)-1))
# generar observaciones de series de tiempo con influencias aleatorias
for (i in 2:length(Date)) {
X[i] <- -50 + 0.98 * X[i-1] + rnorm(n = 1, sd = 200)
}
# trazar los resultados
plot(x = Date,
y = X,
type = "l",
col = "steelblue",
ylab = "Trabajadores",
xlab = "Tiempo")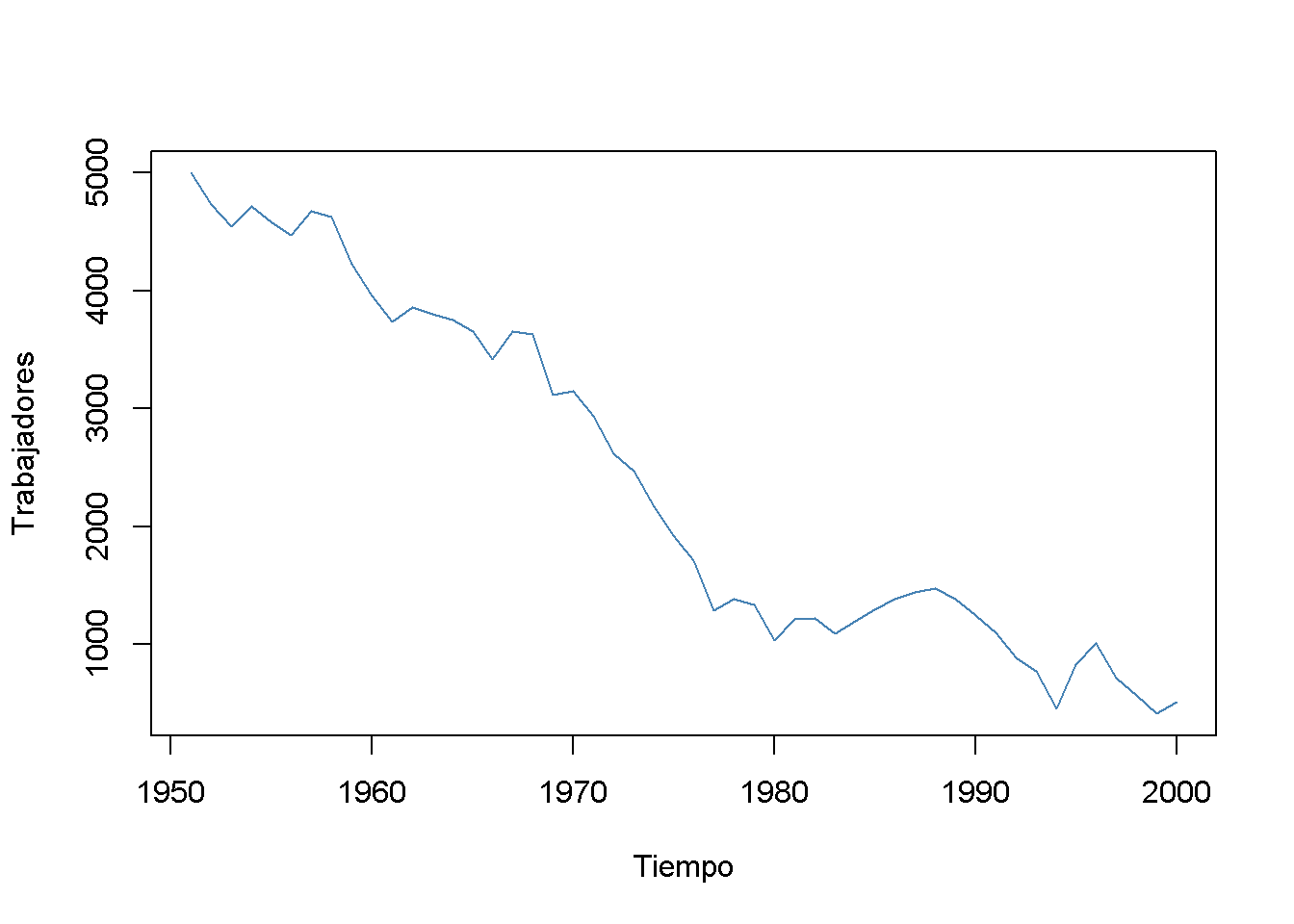
Es evidente que las observaciones sobre el número de empleados no pueden ser independientes en este ejemplo: el nivel de empleo de hoy está correlacionado con el nivel de empleo de mañana. Por lo tanto, se viola la suposición de i.i.d.
Supuesto 3: Los valores atípicos grandes son poco probables
Es fácil pensar en situaciones en las que pueden ocurrir observaciones extremas; es decir, observaciones que se desvían considerablemente del rango habitual de datos. Estas observaciones se denominan valores atípicos. Técnicamente hablando, el supuesto 3 requiere que \(X\) y \(Y\) tengan una curtosis finita.2.
Los casos comunes en los que se quiere excluir o (si es posible) corregir dichos valores atípicos son cuando aparentemente son errores tipográficos, errores de conversión o errores de medición. Incluso si parece que las observaciones extremas se han registrado correctamente, es aconsejable excluirlas antes de estimar un modelo, ya que MCO adolece de sensibilidad a valores atípicos.
¿Qué significa esto? Se puede demostrar que las observaciones extremas reciben una gran ponderación en la estimación de los coeficientes de regresión desconocidos cuando se utiliza MCO. Por lo tanto, los valores atípicos pueden dar lugar a estimaciones de los coeficientes de regresión muy distorsionadas. Para tener una mejor impresión de este problema, considere la siguiente aplicación donde se han colocado algunos datos de muestra en \(X\) y \(Y\) que están altamente correlacionados. La relación entre \(X\) y \(Y\) parece explicarse bastante bien por la línea de regresión trazada: todos los puntos de datos blancos se encuentran cerca de la línea de regresión roja y se tiene \(R^2 = 0.92\).
Ahora continúe y agregue una observación adicional en, digamos, \((18, 2)\). Esta observación claramente es un caso atípico. El resultado es bastante sorprendente: la línea de regresión estimada difiere mucho de la que se considera que se ajusta bien a los datos. ¡La pendiente está fuertemente sesgada a la baja y \(R^2\) disminuyó a solo \(29\%\)!
Haga doble clic dentro del sistema de coordenadas para restablecer la aplicación. Siéntase libre de experimentar. Elija diferentes coordenadas para el valor atípico o agregue otras adicionales.
En el siguiente código se usan datos de muestra generados usando las funciones de números aleatorios de R: rnorm() y runif(). Se estiman dos modelos de regresión simple, uno basado en el conjunto de datos original y otro usando un conjunto modificado donde una observación cambia para ser un valor atípico y luego se grafican los resultados. Para comprender el código completo, debe estar familiarizado con la función sort() que ordena las entradas de un vector numérico en orden ascendente.
# sembrar semilla
set.seed(123)
# generar los datos
X <- sort(runif(10, min = 30, max = 70))
Y <- rnorm(10 , mean = 200, sd = 50)
Y[9] <- 2000
# ajustar modelo con valor atípico
fit <- lm(Y ~ X)
# ajuste del modelo sin valores atípicos
fitWithoutOutlier <- lm(Y[-9] ~ X[-9])
# graficar los resultados
plot(Y ~ X)
abline(fit)
abline(fitWithoutOutlier, col = "red")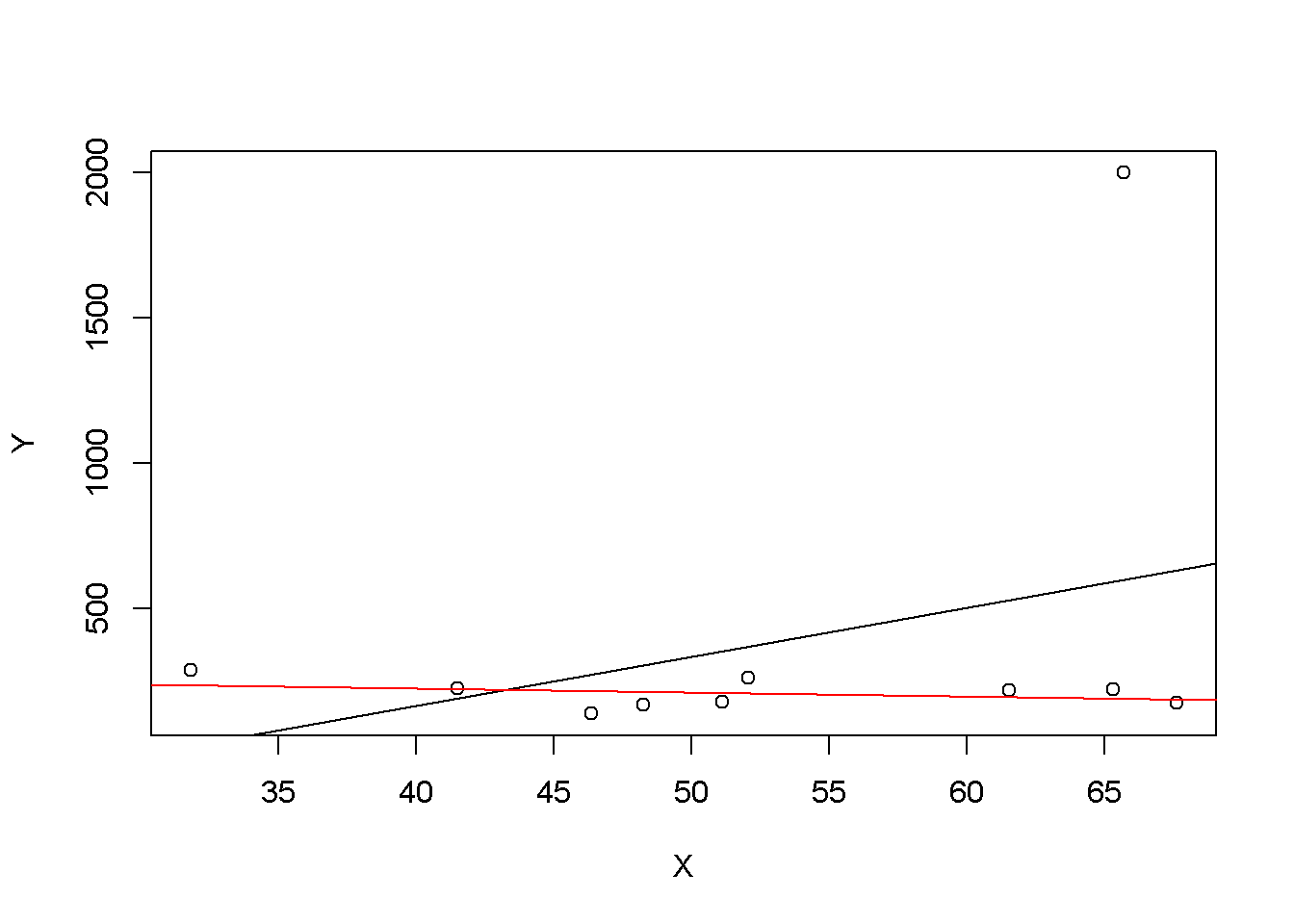
Ver Capítulo 15 para más información sobre autorregresión procesos y análisis de series de tiempo en general.↩︎
La curtosis de una variable estadística/aleatoria es una característica de la forma de su distribución de frecuencias/probabilidad. Según la concepción clásica, una curtosis grande implica una mayor concentración de valores de la variable tanto muy cerca de la media de la distribución (pico) como muy lejos de ella (colas), al tiempo que existe una relativamente menor frecuencia de valores intermedios. Esto explica una forma de la distribución de frecuencias/probabilidad con colas más gruesas, con un centro más apuntado y una menor proporción de valores intermedios entre el pico y colas. Una mayor curtosis no implica una mayor varianza, ni viceversa.↩︎