12.1 Variables dependientes binarias y el modelo de probabilidad lineal
Concepto clave 11.1
El modelo de probabilidad lineal
El modelo de regresión lineal
\[Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \dots + \beta_k X_{ki} + u_i\]
con una variable dependiente binaria \(Y_i\) se denomina modelo de probabilidad lineal. En el modelo de probabilidad lineal se tiene \[E(Y\vert X_1,X_2,\dots,X_k) = P(Y=1\vert X_1, X_2,\dots, X_3)\], donde \[ P(Y = 1 \vert X_1, X_2, \dots, X_k) = \beta_0 + \beta_1 + X_{1i} + \beta_2 X_{2i} + \dots + \beta_k X_{ki}.\]
Por tanto, \(\beta_j\) puede interpretarse como el cambio en la probabilidad de que \(Y_i = 1\), manteniendo constantes los otros regresores \(k-1\). Al igual que en la regresión múltiple común, \(\beta_j\) se puede estimar usando MCO y las fórmulas robustas de error estándar se pueden usar para probar hipótesis y calcular intervalos de confianza.
En la mayoría de los modelos de probabilidad lineal, \(R^2\) no tiene una interpretación significativa ya que la línea de regresión nunca puede ajustarse perfectamente a los datos si la variable dependiente es binaria y los regresores son continuos. Esto se puede ver en la aplicación a continuación.
Es esencial utilizar errores estándar robustos, ya que los \(u_i\), en un modelo de probabilidad lineal, son siempre heterocedásticos.
Los modelos de probabilidad lineal se estiman fácilmente en R usando la función lm().
Datos hipotecarios
Se debe comenzar cargando el conjunto de datos HMDA que proporciona datos relacionados con las solicitudes de hipotecas presentadas en Boston en el año de 1990.
# cargar el paquete `AER` y adjuntar los datos de "HMDA"
library(AER)
data(HMDA)Se continuan inspeccionando las primeras observaciones y luego calculando las estadísticas resumidas.
# inspeccionar los datos
head(HMDA)
#> deny pirat hirat lvrat chist mhist phist unemp selfemp insurance condomin
#> 1 no 0.221 0.221 0.8000000 5 2 no 3.9 no no no
#> 2 no 0.265 0.265 0.9218750 2 2 no 3.2 no no no
#> 3 no 0.372 0.248 0.9203980 1 2 no 3.2 no no no
#> 4 no 0.320 0.250 0.8604651 1 2 no 4.3 no no no
#> 5 no 0.360 0.350 0.6000000 1 1 no 3.2 no no no
#> 6 no 0.240 0.170 0.5105263 1 1 no 3.9 no no no
#> afam single hschool
#> 1 no no yes
#> 2 no yes yes
#> 3 no no yes
#> 4 no no yes
#> 5 no no yes
#> 6 no no yes
summary(HMDA)
#> deny pirat hirat lvrat chist
#> no :2095 Min. :0.0000 Min. :0.0000 Min. :0.0200 1:1353
#> yes: 285 1st Qu.:0.2800 1st Qu.:0.2140 1st Qu.:0.6527 2: 441
#> Median :0.3300 Median :0.2600 Median :0.7795 3: 126
#> Mean :0.3308 Mean :0.2553 Mean :0.7378 4: 77
#> 3rd Qu.:0.3700 3rd Qu.:0.2988 3rd Qu.:0.8685 5: 182
#> Max. :3.0000 Max. :3.0000 Max. :1.9500 6: 201
#> mhist phist unemp selfemp insurance condomin
#> 1: 747 no :2205 Min. : 1.800 no :2103 no :2332 no :1694
#> 2:1571 yes: 175 1st Qu.: 3.100 yes: 277 yes: 48 yes: 686
#> 3: 41 Median : 3.200
#> 4: 21 Mean : 3.774
#> 3rd Qu.: 3.900
#> Max. :10.600
#> afam single hschool
#> no :2041 no :1444 no : 39
#> yes: 339 yes: 936 yes:2341
#>
#>
#>
#> La variable que interesa modelar es deny, un indicador de si la solicitud de hipoteca de un solicitante ha sido aceptada (deny = no) o denegada (deny = yes). Un regresor que debería tener poder para explicar si una solicitud de hipoteca ha sido denegada es pirat, el tamaño de los pagos mensuales totales anticipados del préstamo en relación con los ingresos del solicitante. Es sencillo traducir esto al modelo de regresión simple
\[\begin{align} deny = \beta_0 + \beta_1 \times P/I\ ratio + u. \tag{12.1} \end{align}\]
Se estima este modelo como cualquier otro modelo de regresión lineal utilizando lm(). Antes de hacerlo, la variable deny debe convertirse en una variable numérica usando as.numeric(), ya que lm() no acepta que la variable dependiente sea de la clase factor. Se debe tener en cuenta que as.numeric(HMDA$deny) convertirá deny = no en deny = 1 y deny = yes en deny = 2, por lo que al usar as.numeric(HMDA$deny)-1 se obtienen los valores 0 y 1.
# convertir 'deny' a numérico
HMDA$deny <- as.numeric(HMDA$deny) - 1
# estimar un modelo de probabilidad lineal simple
denymod1 <- lm(deny ~ pirat, data = HMDA)
denymod1
#>
#> Call:
#> lm(formula = deny ~ pirat, data = HMDA)
#>
#> Coefficients:
#> (Intercept) pirat
#> -0.07991 0.60353A continuación, se grafican los datos y la línea de regresión.
# graficar los datos
plot(x = HMDA$pirat,
y = HMDA$deny,
main = "Diagrama de dispersión denegación de solicitud de hipoteca y relación pago-ingreso",
xlab = "Relación P/I",
ylab = "Denegar",
pch = 20,
ylim = c(-0.4, 1.4),
cex.main = 0.8)
# añadir texto y líneas discontinuas horizontales
abline(h = 1, lty = 2, col = "darkred")
abline(h = 0, lty = 2, col = "darkred")
text(2.5, 0.9, cex = 0.8, "Hipoteca denegada")
text(2.5, -0.1, cex= 0.8, "Hipoteca aprobada")
# agregar la línea de regresión estimada
abline(denymod1,
lwd = 1.8,
col = "steelblue")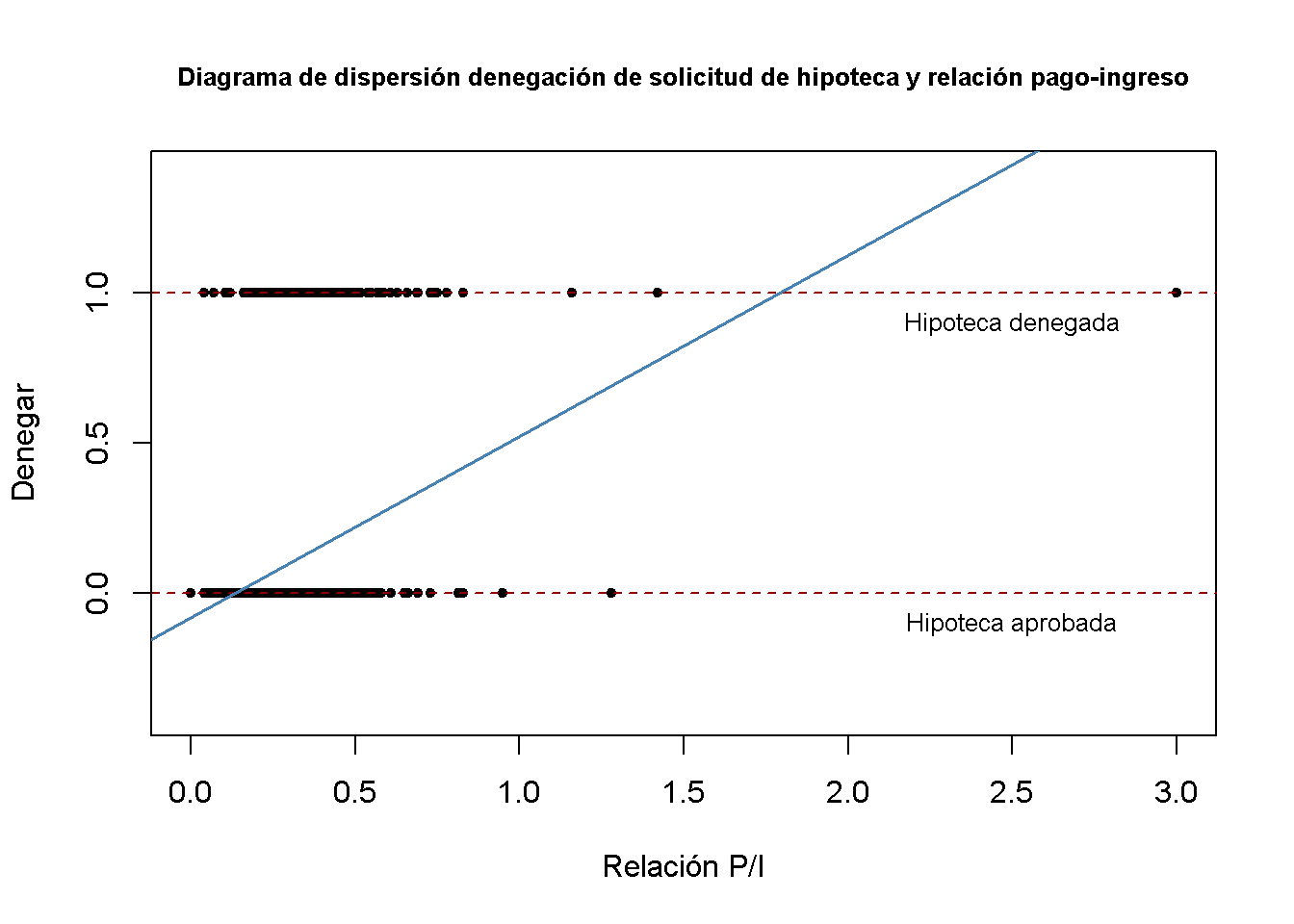
Según el modelo estimado, una relación pago-ingresos de \(1\) se asocia con una probabilidad esperada de denegación de la solicitud de hipoteca de aproximadamente \(50\%\). El modelo indica que existe una relación positiva entre la relación pago-ingresos y la probabilidad de una solicitud hipotecaria denegada, por lo que es más probable que las personas con una alta relación entre pagos de préstamos e ingresos sean rechazadas.
Se puede usar coeftest() para obtener errores estándar robustos para ambas estimaciones de coeficientes.
# imprimir un resumen robusto de coeficientes
coeftest(denymod1, vcov. = vcovHC, type = "HC1")
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.079910 0.031967 -2.4998 0.01249 *
#> pirat 0.603535 0.098483 6.1283 1.036e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La línea de regresión estimada es:
\[\begin{align} \widehat{\text{denegar}} = -\underset{(0.032)}{0.080} + \underset{(0.098)}{0.604} P/I \ ratio. \tag{12.2} \end{align}\]
El verdadero coeficiente de \(P/I \ ratio\) es estadísticamente diferente de \(0\) en el nivel de \(1\%\). Su estimación se puede interpretar de la siguiente manera: Un aumento de un punto porcentual en \(P/I \ ratio\) conduce a un aumento en la probabilidad de denegación de un préstamo en \(0.604 \cdot 0.01 = 0.00604 \approx 0.6\%\).
En este sentido, se aumenta el modelo simple (12.1) con un regresor adicional \(black\) que equivale a \(1\) si el solicitante es afroamericano y equivale a \(0\) en caso contrario. Dicha especificación es la línea de base para investigar si existe discriminación racial en el mercado hipotecario: Si ser negro tiene una influencia significativa (positiva) en la probabilidad de denegación de un préstamo cuando se controlan los factores que permiten una evaluación objetiva y digna del crédito de un solicitante, este es un indicador de discriminación.
# cambiar el nombre de la variable 'afam' por coherencia
colnames(HMDA)[colnames(HMDA) == "afam"] <- "black"
# estimar el modelo
denymod2 <- lm(deny ~ pirat + black, data = HMDA)
coeftest(denymod2, vcov. = vcovHC)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.090514 0.033430 -2.7076 0.006826 **
#> pirat 0.559195 0.103671 5.3939 7.575e-08 ***
#> blackyes 0.177428 0.025055 7.0815 1.871e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La función de regresión estimada es
\[\begin{align} \widehat{\text{denegar}} =& \, -\underset{(0.029)}{0.091} + \underset{(0.089)}{0.559} P/I \ ratio + \underset{(0.025)}{0.177} black. \tag{12.3} \end{align}\]
El coeficiente de \(black\) es positivo y significativamente diferente de cero en el nivel de \(0.01\%\). La interpretación es que, manteniendo constante la relación \(P/I \ ratio\), ser negro aumenta la probabilidad de denegación de una solicitud de hipoteca en aproximadamente \(17.7\%\). Este hallazgo es compatible con la discriminación racial. Sin embargo, podría estar distorsionado por el sesgo de la variable omitida, por lo que la discriminación podría ser una conclusión prematura.