16.5 Estimación de efectos causales dinámicos con regresores estrictamente exógenos
En general, los errores en un modelo de retardo distribuido están correlacionados, lo que requiere el uso de errores estándar de HAC para una inferencia válida. Sin embargo, si la suposición de exogeneidad (la primera suposición establecida en el Concepto clave 15.1) se reemplaza por exogeneidad estricta, es \[E(u_t\vert \dots, X_{t+1}, X_{t}, X_{t-1}, \dots) = 0,\] se encuentran disponibles enfoques más eficientes que la estimación MCO de los coeficientes. Para un modelo de rezago distribuido general con \(r\) rezagos y errores AR(\(p\)), estos enfoques se resumen en el Concepto clave 15.4.
Concepto clave 15.4
Estimación de multiplicadores dinámicos bajo estricta exogeneidad
Considere el modelo de retraso distribuido general con \(r\) retrasos y errores después de un proceso AR(\(p\)),
\[\begin{align} Y_t =& \, \beta_0 + \beta_1 X_t + \beta_2 X_{t-1} + \dots + \beta_{r+1} X_{t-r} + u_t \tag{16.7} \\ u_t =& \, \phi_1 u_{t-1} + \phi u_{t-2} + \dots + \phi_p u_{t-p} + \overset{\sim}{u}_t. \tag{16.8} \end{align}\]
Bajo exogeneidad estricta de \(X_t\), se puede reescribir el modelo anterior en la especificación ADL
\[\begin{align*} Y_t =& \, \alpha_0 + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \dots + \phi_p Y_{t-p} \\ &+ \, \delta_0 X_t + \delta_1 X_{t-1} + \dots + \delta_q X_{t-q} + \overset{\sim}{u}_t \end{align*}\]
donde \(q=r+p\) y calcular estimaciones de los multiplicadores dinámicos \(\beta_1, \beta_2, \dots, \beta_{r+1}\) utilizando estimaciones de MCO de \(\phi_1, \phi_2, \dots, \phi_p, \delta_0, \delta_1, \dots, \delta_q\).
Una alternativa es estimar los multiplicadores dinámicos utilizando MCG factible; es decir, aplicar el estimador MCO a una especificación de cuasi-diferencia de (16.7). Bajo exogeneidad estricta, el enfoque MCG factible es el estimador AZUL para los multiplicadores dinámicos en muestras grandes.
Por un lado, la estimación por MCO de la representación de AVD puede ser beneficiosa para la estimación de los multiplicadores dinámicos en modelos de rezagos distribuidos grandes porque permite un modelo más parsimonioso que puede ser una buena aproximación al modelo grande. Por otro lado, el enfoque MCG es más eficiente que el estimador de AVD si el tamaño de la muestra es grande.
En breve se revisa cómo se pueden obtener las diferentes representaciones de un modelo de retardo distribuido pequeño y se muestra cómo se puede estimar esta especificación mediante MCO y MCG usando R.
El modelo es
\[\begin{align} Y_t = \beta_0 + \beta_1 X_t + \beta_2 X_{t-1} + u_t, \tag{16.9} \end{align}\]
por lo que se modela un cambio en \(X\) para que afecte a \(Y\) simultáneamente (\(\beta_1\)) y en el siguiente período (\(\beta_2\)). Se supone que el término de error \(u_t\) sigue un proceso AR(\(1\)), \[u_t = \phi_1 u_{t-1} + \overset{\sim}{u_t},\] donde \(\overset{\sim}{u_t}\) no está correlacionado en serie.
Se puede demostrar que la representación de ADL de este modelo es
\[\begin{align} Y_t = \alpha_0 + \phi_1 Y_{t-1} + \delta_0 X_t + \delta_1 X_{t-1} + \delta_2 X_{t-2} + \overset{\sim}{u}_t, \tag{16.10} \end{align}\]
con las restricciones
\[\begin{align*} \beta_1 =& \, \delta_0, \\ \beta_2 =& \, \delta_1 + \phi_1 \delta_0, \end{align*}\]
Cuasi-diferencias
Otra forma de escribir la representación de ADL(\(1\),\(2\)) (16.10) es el modelo de cuasi-diferencia
\[\begin{align} \overset{\sim}{Y}_t = \alpha_0 + \beta_1 \overset{\sim}{X}_t + \beta_2 \overset{\sim}{X}_{t-1} + \overset{\sim}{u}_t, \tag{16.11} \end{align}\]
donde \(\overset{\sim}{Y}_t = Y_t - \phi_1 Y_{t-1}\) y \(\overset{\sim}{X}_t = X_t - \phi_1 X_{t-1}\) Observe que el término de error \(\overset{\sim}{u}_t\) no está correlacionado en ambos modelos y \[E(u_t\vert X_{t+1}, X_t, X_{t-1}, \dots) = 0,\] que está implícito en el supuesto de exogeneidad estricta.
Se continua simulando una serie de tiempo de observaciones de \(500\) usando el modelo (16.9) con \(\beta_1 = 0.1\), \(\beta_2 = 0.25\), \(\phi = 0.5\) y \(\overset{\sim}{u}_t \sim \mathcal{N}(0,1)\), así como estimar las diferentes representaciones, comenzando con el modelo de retardo distribuido (16.9).
# sembrar la semilla para la reproducibilidad
set.seed(1)
# simular una serie de tiempo con errores correlacionados en serie
obs <- 501
eps <- arima.sim(n = obs-1 , model = list(ar = 0.5))
X <- arima.sim(n = obs, model = list(ar = 0.25))
Y <- 0.1 * X[-1] + 0.25 * X[-obs] + eps
X <- ts(X[-1])
# estimar el modelo de rezago distribuido
dlm <- dynlm(Y ~ X + L(X))Comprobar que los residuos de este modelo exhiben autocorrelación usando acf().
# comprobar que los residuales estén correlacionados en serie
acf(residuals(dlm))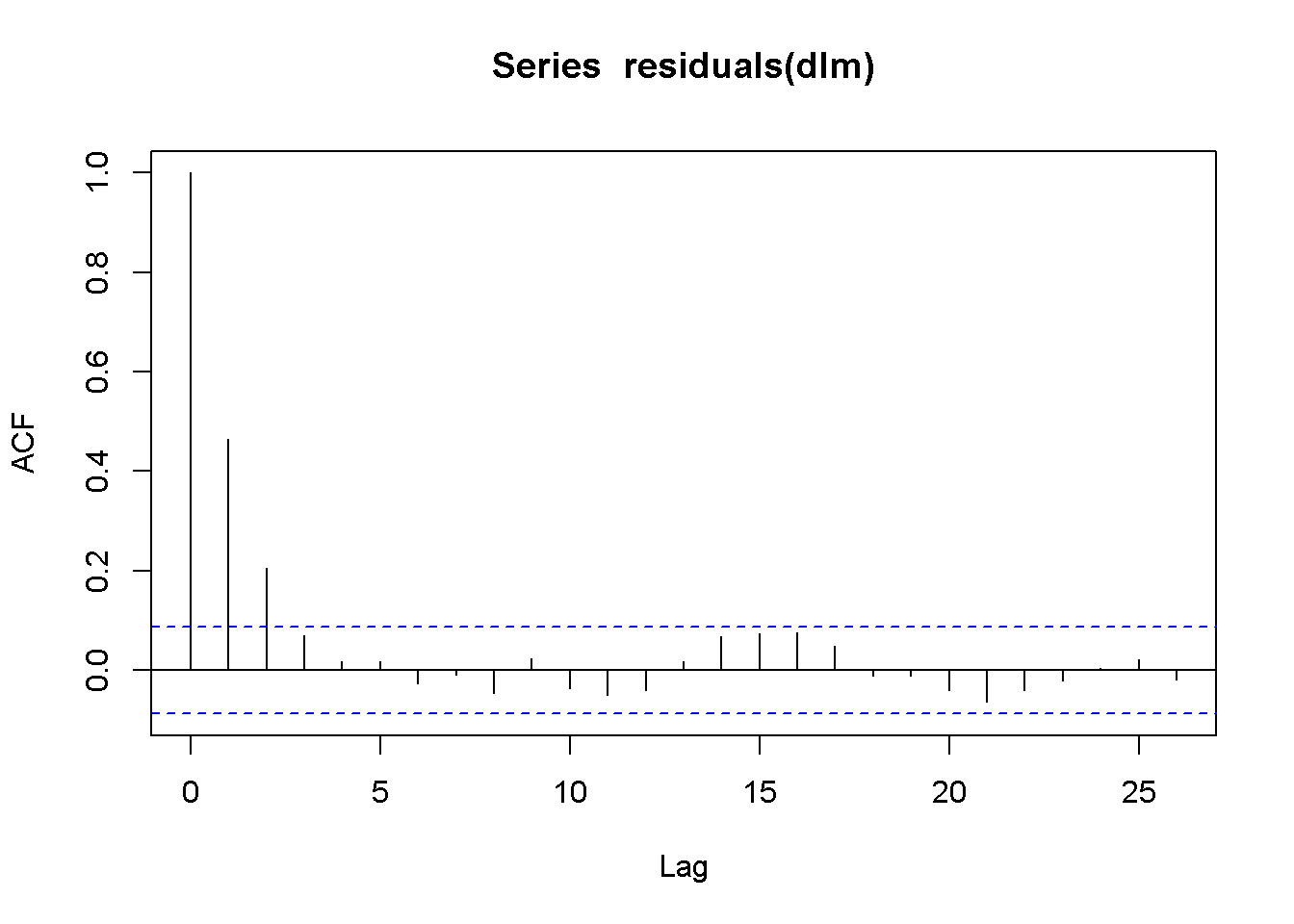
En particular, el patrón revela que los residuos siguen un proceso autorregresivo, ya que la función de autocorrelación de la muestra decae rápidamente durante los primeros rezagos y probablemente sea cero para los órdenes de rezago más altos. En cualquier caso, deben utilizarse errores estándar de HAC.
# resumen de coeficientes utilizando las estimaciones de errores estándar de Newey-West
coeftest(dlm, vcov = NeweyWest, prewhite = F, adjust = T)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.038340 0.073411 0.5223 0.601717
#> X 0.123661 0.046710 2.6474 0.008368 **
#> L(X) 0.247406 0.046377 5.3347 1.458e-07 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Estimación MCO del modelo ADL
A continuación, se estima el modelo ADL(\(1\),\(2\)) (16.10) usando MCO. Los errores no están correlacionados en esta representación del modelo. Esta afirmación está respaldada por un gráfico de la función de autocorrelación muestral de la serie residual.
# estimar la representación de ADL(2,1) del modelo de rezago distribuido
adl21_dynamic <- dynlm(Y ~ L(Y) + X + L(X, 1:2))
# graficar las autocorrelaciones de muestra de residuos
acf(adl21_dynamic$residuals)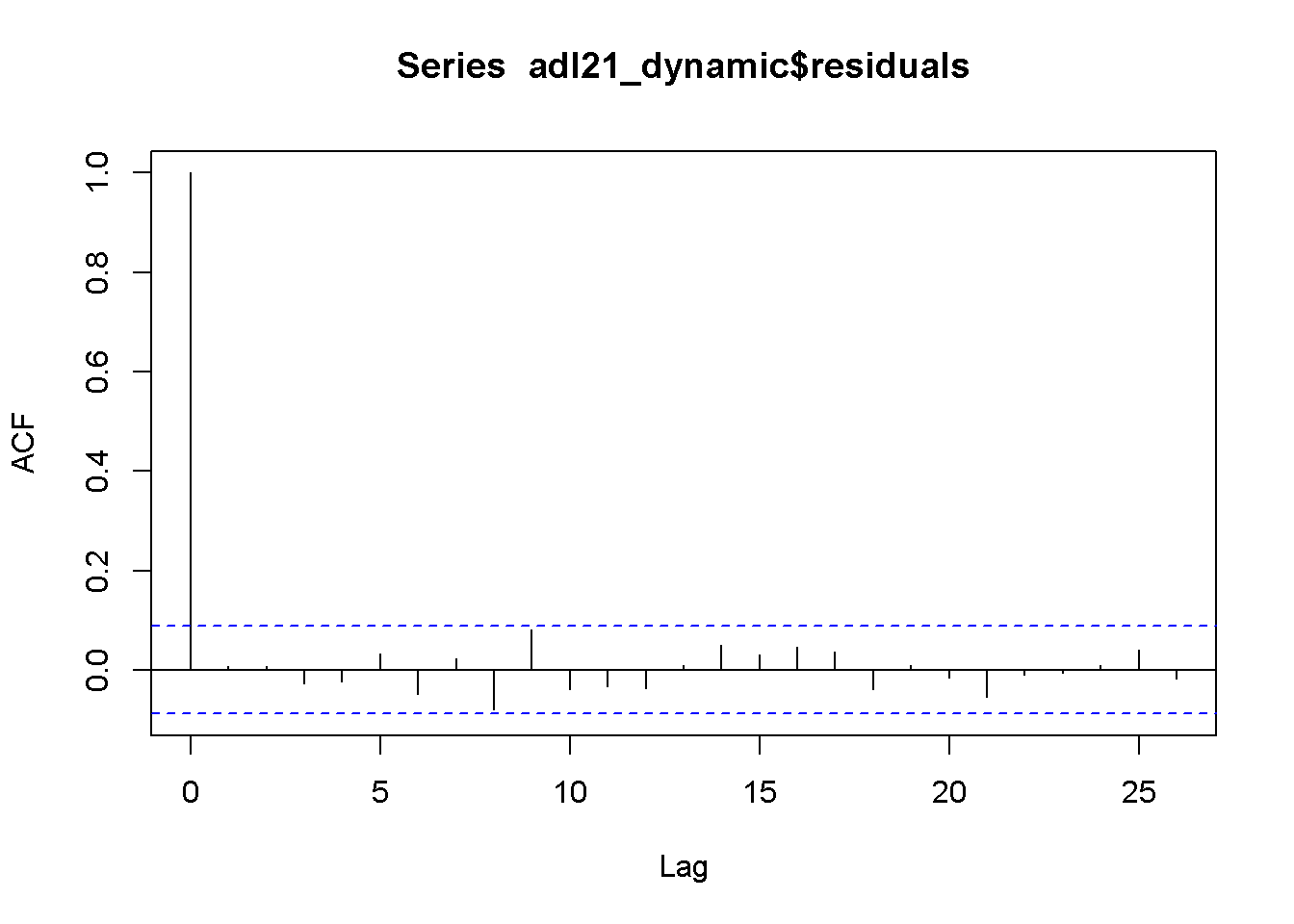
Los coeficientes estimados de adl21_dynamic$coefficients no son los multiplicadores dinámicos que interesan, sino que pueden calcularse de acuerdo con las restricciones en (16.10), donde los coeficientes verdaderos son reemplazados por las estimaciones de MCO.
# calcular efectos dinámicos estimados usando restricciones de coeficientes
# en la representación de ADL(2,1)
t <- adl21_dynamic$coefficients
c("hat_beta_1" = t[3],
"hat_beta_2" = t[4] + t[3] * t[2])
#> hat_beta_1.X hat_beta_2.L(X, 1:2)1
#> 0.1176425 0.2478484Estimación de mínimos cuadrados generalizados (MCG)
La exogeneidad estricta permite la estimación por MCO del modelo de cuasi-diferencia (16.11). La idea de aplicar el estimador MCO a un modelo donde las variables se transforman linealmente, de modo que los errores del modelo no están correlacionados y son homocedásticos, se denomina mínimos cuadrados generalizados (MCG).
El estimador MCO en (16.11) se llama estimador MCG inviable porque \(\overset{\sim}{Y}\) y \(\overset{\sim}{X}\) no se pueden calcular sin saber \(\phi_1\), el coeficiente autorregresivo en el modelo de error AR(\(1\)), que generalmente se desconoce en la práctica.
Suponga que se sabe que \(\phi = 0.5\). Entonces se pueden obtener las estimaciones MCG inviables de los multiplicadores dinámicos en (16.9) aplicando MCO a los datos transformados.
# MCG: estimación de la especificación cuasi-diferenciada por MCO
iGLS_dynamic <- dynlm(I(Y- 0.5 * L(Y)) ~ I(X - 0.5 * L(X)) + I(L(X) - 0.5 * L(X, 2)))
summary(iGLS_dynamic)
#>
#> Time series regression with "ts" data:
#> Start = 3, End = 500
#>
#> Call:
#> dynlm(formula = I(Y - 0.5 * L(Y)) ~ I(X - 0.5 * L(X)) + I(L(X) -
#> 0.5 * L(X, 2)))
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.0325 -0.6375 -0.0499 0.6658 3.7724
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.01620 0.04564 0.355 0.72273
#> I(X - 0.5 * L(X)) 0.12000 0.04237 2.832 0.00481 **
#> I(L(X) - 0.5 * L(X, 2)) 0.25266 0.04237 5.963 4.72e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.017 on 495 degrees of freedom
#> Multiple R-squared: 0.07035, Adjusted R-squared: 0.0666
#> F-statistic: 18.73 on 2 and 495 DF, p-value: 1.442e-08El estimador MCG factible utiliza una estimación preliminar de los coeficientes en el modelo de término de presunto error, calcula los datos cuasidiferenciados y luego estima el modelo utilizando MCO. Esta idea fue introducida por Cochrane and Orcutt (1949) y puede ampliarse continuando este proceso de forma iterativa. Dicho procedimiento se implementa en la función cochrane.orcutt() del paquete orcutt.
X_t <- c(X[-1])
# crear primer retraso
X_l1 <- c(X[-500])
Y_t <- c(Y[-1])
# procedimiento cochrane-orcutt iterado
summary(cochrane.orcutt(lm(Y_t ~ X_t + X_l1)))
#> Call:
#> lm(formula = Y_t ~ X_t + X_l1)
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.032885 0.085163 0.386 0.69956
#> X_t 0.120128 0.042534 2.824 0.00493 **
#> X_l1 0.252406 0.042538 5.934 5.572e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.0165 on 495 degrees of freedom
#> Multiple R-squared: 0.0704 , Adjusted R-squared: 0.0666
#> F-statistic: 18.7 on 2 and 495 DF, p-value: < 1.429e-08
#>
#> Durbin-Watson statistic
#> (original): 1.06907 , p-value: 1.05e-25
#> (transformed): 1.98192 , p-value: 4.246e-01Algunos métodos más sofisticados para la estimación de MCG se proporcionan con el paquete nlme. La función gls() se puede utilizar para ajustar modelos lineales mediante algoritmos de estimación de máxima verosimilitud y permite especificar una estructura de correlación para el término de error.
# procedimiento factible de estimación de máxima verosimilitud de MCG
summary(gls(Y_t ~ X_t + X_l1, correlation = corAR1()))
#> Generalized least squares fit by REML
#> Model: Y_t ~ X_t + X_l1
#> Data: NULL
#> AIC BIC logLik
#> 1451.847 1472.88 -720.9235
#>
#> Correlation Structure: AR(1)
#> Formula: ~1
#> Parameter estimate(s):
#> Phi
#> 0.4668343
#>
#> Coefficients:
#> Value Std.Error t-value p-value
#> (Intercept) 0.03929124 0.08530544 0.460595 0.6453
#> X_t 0.11986994 0.04252270 2.818963 0.0050
#> X_l1 0.25287471 0.04252497 5.946500 0.0000
#>
#> Correlation:
#> (Intr) X_t
#> X_t 0.039
#> X_l1 0.037 0.230
#>
#> Standardized residuals:
#> Min Q1 Med Q3 Max
#> -3.00075518 -0.64255522 -0.05400347 0.69101814 3.28555793
#>
#> Residual standard error: 1.14952
#> Degrees of freedom: 499 total; 496 residualObserve que en este ejemplo, las estimaciones de coeficientes producidas por MCG están algo más cerca de sus valores verdaderos y que los errores estándar son los más pequeños para el estimador de MCG.