17.2 Órdenes de integración y prueba de raíz unitaria DF-GLS
Algunas series de tiempo económicas tienen tendencias más suaves que las variables que pueden describirse mediante modelos de recorridos aleatorios. Una forma de modelar estas series de tiempo es \[\Delta Y_t = \beta_0 + \Delta Y_{t-1} + u_t,\] donde \(u_t\) es un término de error no correlacionado en serie. Este modelo establece que la primera diferencia de una serie es un paseo aleatorio. En consecuencia, la serie de segundas diferencias de \(Y_t\) es estacionaria. El Concepto clave 16.4 resume la notación.
Concepto clave
16.4
Órdenes de integración, diferenciación y estacionariedad
Cuando una serie de tiempo \(Y_t\) tiene una raíz autorregresiva unitaria, \(Y_t\) se integra de orden uno. Esto a menudo se denota por \(Y_t \sim I(1)\). Simplemente se dice que \(Y_t\) es \(I(1)\). Si \(Y_t\) es \(I(1)\), su primera diferencia \(\Delta Y_t\) es estacionaria.
\(Y_t\) es \(I(2)\) cuando \(Y_t\) necesita diferenciarse dos veces para obtener una serie estacionaria. Usando la notación presentada aquí, si \(Y_t\) es \(I(2)\), su primera diferencia \(\Delta Y_t\) es \(I(1)\) y su segunda diferencia \(\Delta^2 Y_t\) es estacionaria. \(Y_t\) es \(I(d)\) cuando \(Y_t\) debe diferenciarse \(d\) veces para obtener una serie estacionaria.
Cuando \(Y_t\) es estacionario, se integra del orden \(0\) por lo que \(Y_t\) es \(I(0)\).
Es bastante fácil obtener diferencias de series de tiempo en R. Por ejemplo, la función diff() devuelve diferencias adecuadamente rezagadas e iteradas de vectores numéricos, matrices y objetos de series de tiempo de la clase ts.
Se toma el nivel de precios de los EE. UU. Medido por el Índice de precios de gastos de consumo personal como ejemplo.
# definir el objeto ts del índice de precios PCE de EE. UU.
PCECTPI <- ts(log(USMacroSWQ$PCECTPI),
start = c(1957, 1),
end = c(2012, 4),
freq = 4)
# graficar logaritmo del índice de precios de PCE
plot(log(PCECTPI),
main = "Logaritmo del índice de precios PCE de Estados Unidos",
ylab = "Logaritmo",
col = "steelblue",
lwd = 2)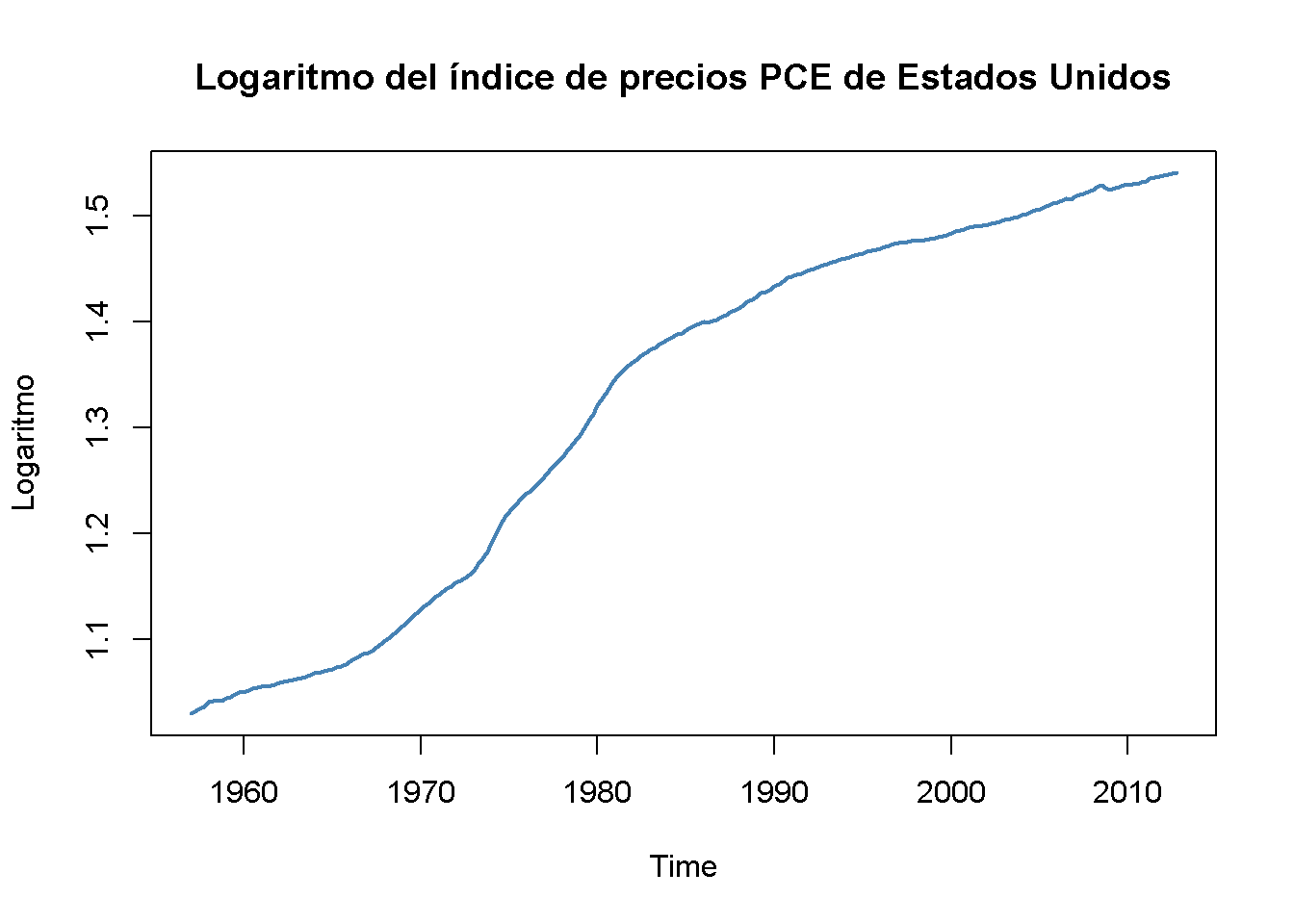
El logaritmo del nivel de precios tiene una tendencia que varía suavemente. Esto es típico de una serie \(I(2)\). Si el nivel de precios es realmente \(I(2)\), las primeras diferencias de esta serie deberían ser \(I(1)\). Dado que se está considerando el logaritmo del nivel de precios, se obtienen tasas de crecimiento tomando las primeras diferencias. Por lo tanto, la serie de niveles de precios diferenciados es la serie de tasas de inflación trimestrales. Esto se hace rápidamente en R usando la función Delt() del paquete quantmod. Como se explica en el Capítulo 15.2, al multiplicar las tasas de inflación trimestrales por \(400\) se obtiene la tasa de inflación trimestral, medida en puntos porcentuales a una tasa anual.
# graficar la inflación de precios del PCE de EE. UU.
plot(400 * Delt(PCECTPI),
main = "United States PCE Price Index",
ylab = "Porcentaje por año",
col = "steelblue",
lwd = 2)
# agregar una línea discontinua en y = 0
abline(0, 0, lty = 2)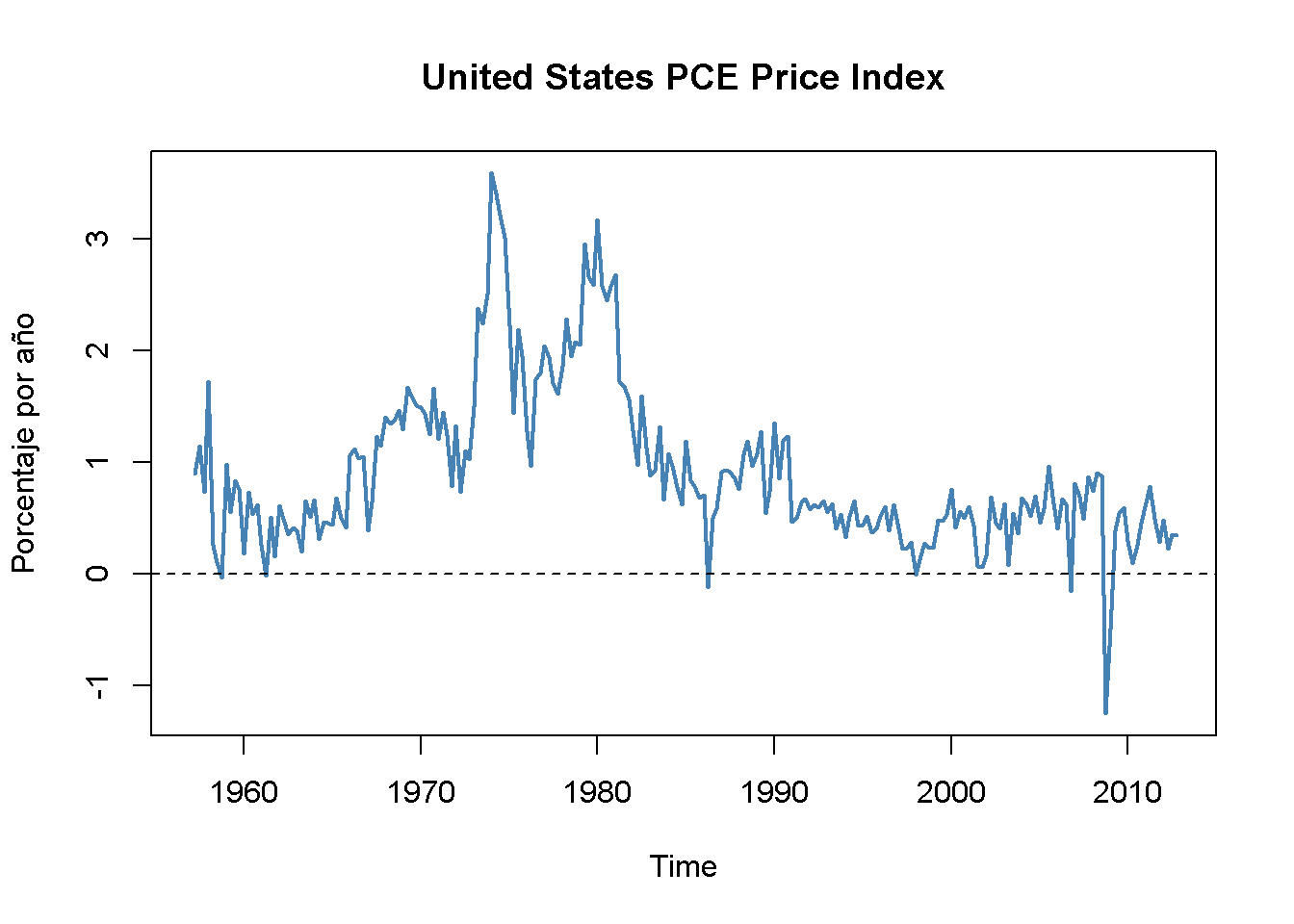
La tasa de inflación se comporta de manera mucho más errática que el gráfico uniforme del logaritmo del índice de precios del PCE.
La prueba DF-GLS para una raíz unitaria
La prueba DF-GLS para una raíz unitaria ha sido desarrollada por Elliott, Rothenberg, and Stock (1996) y tiene mayor potencia que la prueba ADF cuando la raíz autorregresiva es grande, pero menor que uno; es decir, el DF-GLS tiene una mayor probabilidad de rechazar el falso nulo de una tendencia estocástica cuando los datos de la muestra provienen de una serie de tiempo que está cerca de integrarse.
La idea de la prueba DF-GLS es probar una raíz unitaria autorregresiva en la serie sin tendencia, mediante la cual las estimaciones de GLS de los componentes deterministas se utilizan para obtener la versión sin tendencia de la serie original.
Una función que realiza la prueba DF-GLS se implementa en el paquete urca (este paquete es una dependencia del paquete vars, por lo que ya debería estar cargado si se adjunta vars). La función que calcula la estadística de prueba es ur.ers.
# prueba DF-GLS para raíz unitaria en el PIB
summary(ur.ers(log(window(GDP, start = c(1962, 1), end = c(2012, 4))),
model = "trend",
lag.max = 2))
#>
#> ###############################################
#> # Elliot, Rothenberg and Stock Unit Root Test #
#> ###############################################
#>
#> Test of type DF-GLS
#> detrending of series with intercept and trend
#>
#>
#> Call:
#> lm(formula = dfgls.form, data = data.dfgls)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.025739 -0.004054 0.000017 0.004619 0.033620
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> yd.lag -0.01213 0.01012 -1.199 0.23207
#> yd.diff.lag1 0.28583 0.07002 4.082 6.47e-05 ***
#> yd.diff.lag2 0.19320 0.07058 2.737 0.00676 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.007807 on 198 degrees of freedom
#> Multiple R-squared: 0.1504, Adjusted R-squared: 0.1376
#> F-statistic: 11.69 on 3 and 198 DF, p-value: 4.392e-07
#>
#>
#> Value of test-statistic is: -1.1987
#>
#> Critical values of DF-GLS are:
#> 1pct 5pct 10pct
#> critical values -3.48 -2.89 -2.57El resumen de la prueba muestra que el estadístico de la prueba es de aproximadamente \(-1.2\). El valor crítico de $10% $ para la prueba DF-GLS es \(-2.57\). Sin embargo, este no es el valor crítico apropiado para la prueba ADF cuando se incluyen una intersección y una tendencia temporal en la regresión de Dickey-Fuller: ¡Las distribuciones asintóticas de ambas estadísticas de prueba difieren y también sus valores críticos!
La prueba es del lado izquierdo, por lo que no se puede rechazar la hipótesis nula de que la inflación de EE. UU. no es estacionaria, utilizando la prueba DF-GLS.