6.5 El teorema de Gauss-Markov

Al estimar modelos de regresión, se sabe que los resultados del procedimiento de estimación son aleatorios. Sin embargo, al utilizar estimadores insesgados, al menos en promedio, se estima el parámetro verdadero. Por lo tanto, al comparar diferentes estimadores insesgados, es interesante saber cuál tiene la mayor precisión: Siendo conscientes de que la probabilidad de estimar el valor exacto del parámetro de interés es \(0\) en una aplicación empírica, se quiere asegurar que la probabilidad de obtener una estimación muy cercana al valor real es lo más alta posible. Esto implica que se quiere utilizar el estimador con la varianza más baja de todos los estimadores insesgados, siempre que se preocupe por el insesgado. El teorema de Gauss-Markov establece que, en la clase de estimadores lineales condicionalmente insesgados, el estimador MCO tiene esta propiedad bajo ciertas condiciones.

Concepto clave 5.5

El teorema de Gauss-Markov para \(\hat{\beta}_1\)

Suponga que las suposiciones hechas en el Concepto clave 4.3 son válidas y que los errores son homocedásticos. El estimador MCO es el mejor estimador lineal condicionalmente insesgado (AZUL) (en el sentido de la varianza más pequeña) en este entorno.

Echando un vistazo más de cerca a lo que esto significa:

Los estimadores de \(\beta_1\) que son funciones lineales de \(Y_1, \dots, Y_n\) y que son insesgados condicionalmente en el regresor \(X_1, \dots, X_n\) se pueden escribir como \[\overset{\sim}{\beta}_1 = \sum_{i = 1}^n a_i Y_i\]

donde \(a_i\) son pesos que pueden depender de \(X_i\) pero no de \(Y_i\).

Ya se sabe que \(\overset{\sim}{\beta}_1\) tiene una distribución de muestreo: \(\overset{\sim}{\beta}_1\) es una función lineal de \(Y_i\) que son variables aleatorias. Si ahora

\[ E(\overset{\sim}{\beta}_1 | X_1, \dots, X_n) = \beta_1,\]

\(\overset{\sim}{\beta}_1\) es un estimador lineal imparcial de \(\beta_1\), condicionalmente en \(X_1, \dots, X_n\).

Se puede preguntar si \(\overset{\sim}{\beta}_1\) es también el mejor estimador de esta clase; es decir, el más eficiente de todos los estimadores lineales condicionalmente insesgados donde “más eficiente” significa varianza más pequeña. Los pesos \(a_i\) juegan un papel importante aquí y resulta que MCO usa los pesos correctos para tener la propiedad AZUL.

Estudio de simulación: Estimador AZUL

Considere el caso de una regresión de \(Y_i,\dots,Y_n\) solo en una constante. Aquí, se supone que \(Y_i\) es una muestra aleatoria de una población con media \(\mu\) y varianza \(\sigma^2\). El estimador de MCO en este modelo es simplemente la media de la muestra, consulte el Capítulo 4.2.

\[\begin{equation} \hat{\beta}_1 = \sum_{i=1}^n \underbrace{\frac{1}{n}}_{=a_i} Y_i \tag{6.3} \end{equation}\]

Claramente, cada observación está ponderada por

\[a_i = \frac{1}{n}.\]

y también se sabe que \(\text{Var}(\hat{\beta}_1)=\frac{\sigma^2}{n}\).

Ahora se usa R para realizar un estudio de simulación que demuestra lo que sucede con la varianza de (6.3) si diferentes pesos \(w_i = \frac{1 \pm \epsilon}{n}\) se asignan a la mitad de la muestra \(Y_1, \dots, Y_n\) en lugar de usar \(\frac{1}{n}\), los pesos de MCO.

# establecer el tamaño de la muestra y el número de repeticiones
n <- 100      
reps <- 1e5

# elegir épsilon y crear un vector de pesos como se define arriba
epsilon <- 0.8
w <- c(rep((1 + epsilon) / n, n / 2), 
       rep((1 - epsilon) / n, n / 2) )

# extraer una muestra aleatoria y_1, ..., y_n de la distribución normal estándar,
# usar ambos estimadores 1e5 veces y almacene el resultado en los vectores 'ols' y
# 'weightedestimator'

ols <- rep(NA, reps)
weightedestimator <- rep(NA, reps)

for (i in 1:reps) {
  
  y <- rnorm(n)
  ols[i] <- mean(y)
  weightedestimator[i] <- crossprod(w, y)
  
}

# graficar estimaciones de densidad de kernel de las distribuciones de los estimadores:
# MCO
plot(density(ols), 
     col = "purple", 
     lwd = 3, 
     main = "Densidad de MCO y estimador ponderado",
     xlab = "Estimados")

# ponderado
lines(density(weightedestimator), 
      col = "steelblue", 
      lwd = 3) 

# agregar una línea discontinua en 0 y agregar una leyenda al gráfico
abline(v = 0, lty = 2)

legend('topright', 
       c("MCO", "ponderado"), 
       col = c("purple", "steelblue"), 
       lwd = 3)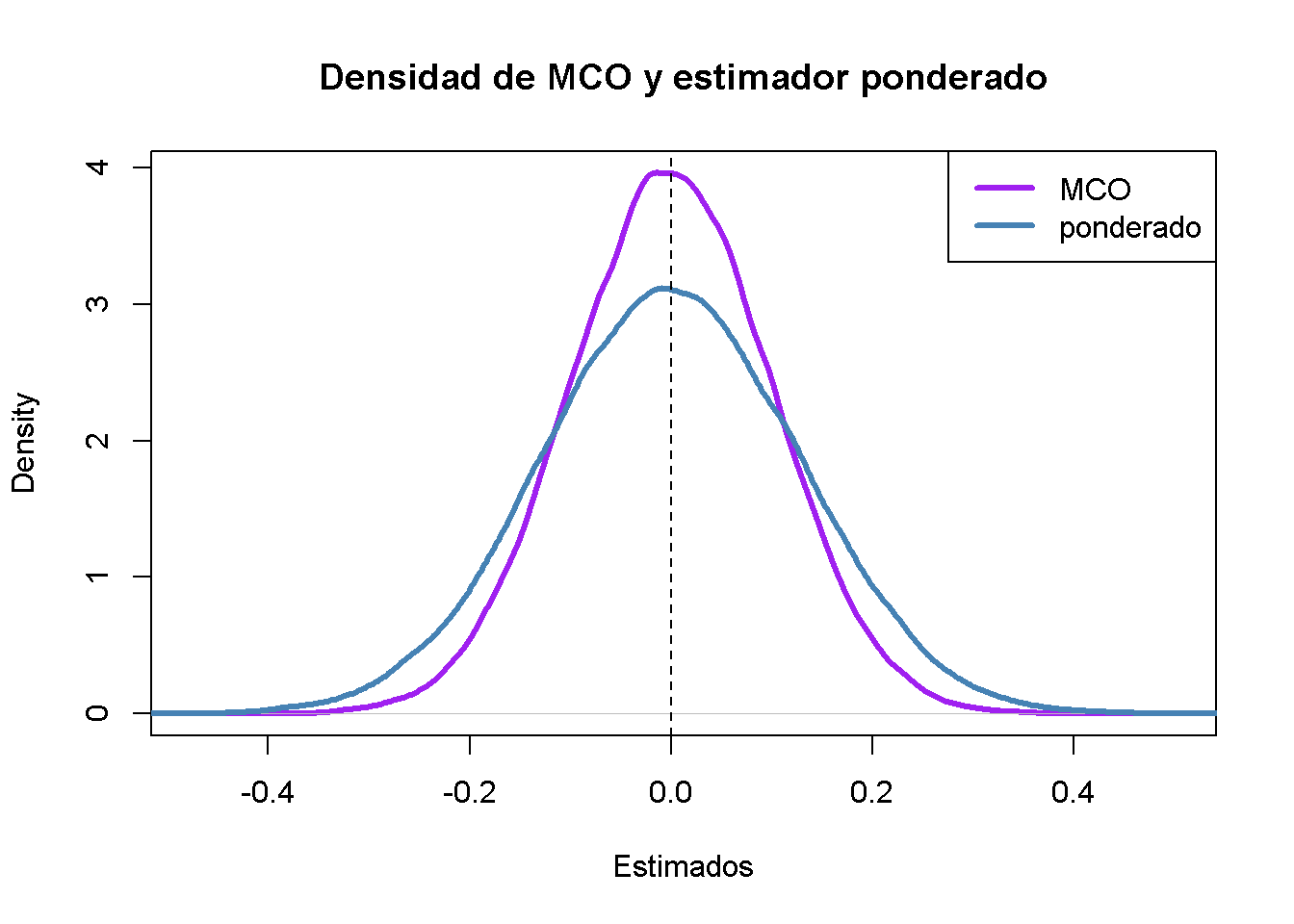

¿Qué conclusión se puede obtener del resultado?

Ambos estimadores parecen no sesgados: Las medias de sus distribuciones estimadas son cero.
El estimador que usa ponderaciones que se desvían de las implícitas en los MCO es menos eficiente que el estimador MCO: Existe una mayor dispersión cuando las ponderaciones son \(w_i = \frac{1 \pm 0.8}{100}\) en lugar de \(w_i=\frac{1}{100}\) según lo requiera la solución MCO.

Por tanto, los resultados de la simulación apoyan el teorema de Gauss-Markov.