6.3 Regresión cuando X es una variable binaria

En lugar de usar un regresor continuo $X$, de podría estar interesados en ejecutar la regresión

$Y_i = \beta_0 + \beta_1 D_i + u_i \tag{5.2}$

donde $D_i$ es una variable binaria, una llamada variable ficticia (dummy variable). Por ejemplo, se puede definir $D_i$ de la siguiente manera:

$D_i = \begin{cases} 1 \ \ \text{si $STR$ en $i^{ésimo}$ distrito escolar < 20} \\ 0 \ \ \text{si $STR$ en $i^{ésimo}$ distrito escolar $\geq$ 20} \\ \end{cases} \tag{5.3}$

El modelo de regresión ahora es

$TestScore_i = \beta_0 + \beta_1 D_i + u_i. \tag{5.4}$

Es momento de ver cómo se comportan estos datos en un diagrama de dispersión:

# Cree la variable ficticia como se define arriba
CASchools$D <- CASchools$STR < 20

# Graficar los datos
plot(CASchools$D, CASchools$score,     # proporciona los datos que se trazarán
     pch = 20,                         # utilizar círculos rellenos como símbolos de la gráfica
     cex = 0.5,                        # establecer el tamaño de los símbolos de la gráfica en 0.5
     col = "Steelblue",                # establece el color de los símbolos en "Steelblue"
     xlab = expression(D[i]),          # establecer el título y los nombres de los ejes
     ylab = "Resultado de la prueba",
     main = "Regresión ficticia")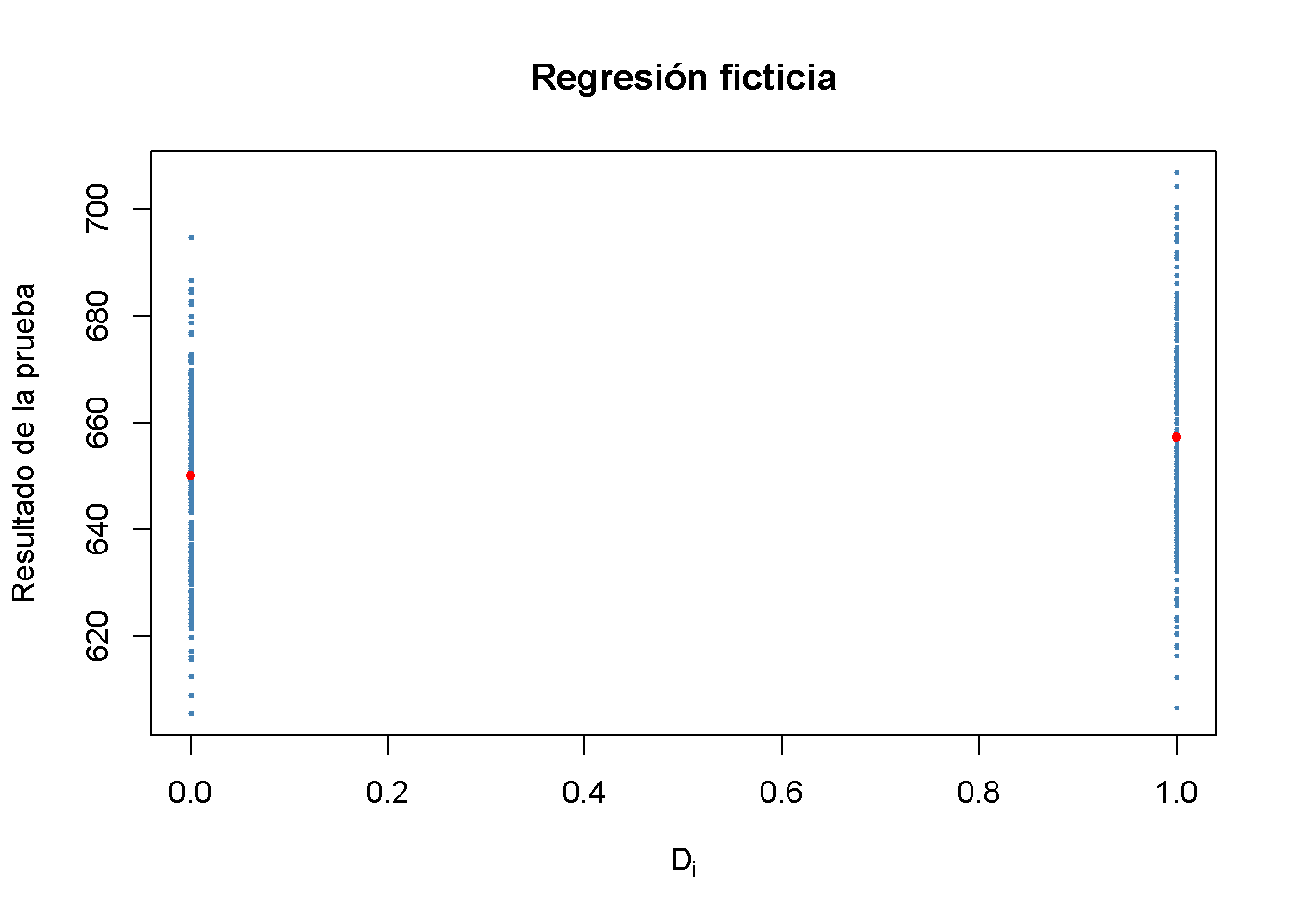

Con $D$ como regresor, no es útil pensar en $\beta_1$ como un parámetro de pendiente, ya que $D_i \in \{0,1\}$; es decir, solo se observan dos valores discretos en lugar de un continuo de valores regresores. No hay una línea continua que represente la función de expectativa condicional $E(TestScore_i | D_i)$, teniendo en cuenta que esta función está definida únicamente para $x$ - en las posiciones $0$ y $1$.

Por tanto, la interpretación de los coeficientes en este modelo de regresión es la siguiente:

$E(Y_i | D_i = 0) = \beta_0$, por lo que $\beta_0$ es la puntuación de prueba esperada en los distritos donde $D_i = 0$ donde $STR$ está por encima de $20$.
$E(Y_i | D_i = 1) = \beta_0 + \beta_1$ o, usando el resultado anterior, $\beta_1 = E(Y_i | D_i = 1) - E(Y_i | D_i = 0)$. Por lo tanto, $\beta_1$ es la diferencia en las expectativas específicas del grupo; es decir, la diferencia en la puntuación esperada de la prueba entre los distritos con $STR<20$ y aquellos con $STR\geq20$.

Ahora se usará R para estimar un modelo de regresión ficticio según lo definido por las ecuaciones (5.2) y (5.3).

# estimar el modelo de regresión ficticia
dummy_model <- lm(score ~ D, data = CASchools)
summary(dummy_model)
#> 
#> Call:
#> lm(formula = score ~ D, data = CASchools)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -50.496 -14.029  -0.346  12.884  49.504 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  650.077      1.393 466.666  < 2e-16 ***
#> DTRUE          7.169      1.847   3.882  0.00012 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 18.74 on 418 degrees of freedom
#> Multiple R-squared:  0.0348, Adjusted R-squared:  0.0325 
#> F-statistic: 15.07 on 1 and 418 DF,  p-value: 0.0001202

summary() informa el valor $p$ de la prueba, que en este caso el coeficiente en (Intercepción) es cero para ser <2e-16. Esta notación científica establece que el valor $p$ es menor que $\frac{2}{10^{16}}$, por lo que es un número muy pequeño. La razón de esto es que las computadoras no pueden manejar números pequeños arbitrarios. De hecho, $\frac{2}{10^{16}}$ es el número más pequeño posible con el que R puede trabajar.

El vector CASchools$D tiene el tipo logical (para ver esto, usar typeof (CASchools$D)) que es mostrado en la salida de summary (modelo_dummy): la etiqueta DTRUE establece que todas las entradas TRUE están codificadas como 1 y todas las entradas FALSE se codifican como 0. Por lo tanto, la interpretación del coeficiente DTRUE es como se indicó anteriormente para $\beta_1$.

Se puede ver como predecir el puntaje de prueba esperado en distritos con $STR < 20$ ($D_i = 1$) será $650.1 + 7.17 = 657.27$ mientras que los distritos con $STR \geq 20$ ($D_i = 0$) se espera que tenga un puntaje promedio de prueba de solo $650.1$.

Las predicciones específicas de grupo se pueden agregar al gráfico mediante la ejecución del siguiente fragmento de código.

# agregar predicciones específicas de grupo a la gráfica
points(x = CASchools$D, 
       y = predict(dummy_model), 
       col = "red", 
       pch = 20)

Aquí se usa la función predict() para obtener estimaciones de las medias específicas del grupo. Los puntos rojos representan los promedios de estos grupos de muestra. En consecuencia, $\hat{\beta}_1 = 7.17$ puede verse como la diferencia en los promedios del grupo.

summary(dummy_model) también responde a la pregunta de si existe una diferencia estadísticamente significativa en las medias de los grupos. Esto, a su vez, apoyaría la hipótesis de que los estudiantes se desempeñan de manera diferente cuando se les enseña en clases pequeñas. Se puede evaluar esto mediante una prueba de dos colas de la hipótesis $H_0: \beta_1 = 0$. Convenientemente, el estadístico $t$ y el valor $p$ correspondiente para esta prueba se calculan mediante summary().

Dado que el valor t $= 3.88 > 1.96$, se rechaza la hipótesis nula en el nivel de significancia de $5\%$. Se obtiene la misma conclusión cuando se usa el valor $p$, que reporta significancia hasta el nivel $0.00012\%$.

Como se hizo con linear_model, alternativamente se puede usar la función confint() para calcular un intervalo de confianza de $95\%$ para la verdadera diferencia en las medias y ver si el valor hipotético es un elemento de este conjunto de confianza.

# intervalos de confianza para coeficientes en el modelo de regresión ficticia
confint(dummy_model)
#>                  2.5 %    97.5 %
#> (Intercept) 647.338594 652.81500
#> DTRUE         3.539562  10.79931

Se rechaza la hipótesis de que no existe diferencia entre las medias de los grupos en el nivel de significancia de $5\%$, ya que $\beta_{1,0} = 0$ se encuentra fuera de $[3.54, 10.8]$, el intervalo de confianza de $95\%$ para el coeficiente de $D$.