16.1 Los datos del jugo de naranja

La región de cultivo de naranjas más grande de los EE. UU. se encuentra en Florida, que generalmente tiene un clima ideal para el crecimiento de la fruta. Por lo tanto, es la fuente de casi todo el concentrado de jugo congelado que se produce en el país. Sin embargo, de vez en cuando y dependiendo de su severidad, las olas de frío provocan una pérdida de cosechas de tal manera que la oferta de naranjas disminuye y en consecuencia sube el precio del concentrado de jugo. El momento de los aumentos de precios es complicado: Un recorte en el suministro actual de concentrado influye no solo en el precio actual, sino también en los precios futuros porque el suministro en períodos futuros también disminuirá. Claramente, la magnitud de los aumentos de precios actuales y futuros debido a la congelación es una pregunta empírica que puede investigarse utilizando un modelo de retardo distribuido, un modelo de series de tiempo que relaciona los cambios de precios con las condiciones climáticas.

Para comenzar con el análisis, se genera una gráfica que muestra el índice de precios del jugo de naranja concentrado congelado, cambios porcentuales en el precio y grados-día de congelación mensuales en Orlando, el centro de la región productora de naranjas de Florida.

# cargar el conjunto de datos de jugo de naranja concentrado congelado
data("FrozenJuice")

# calcular el índice de precios del jugo de naranja concentrado congelado
FOJCPI <- FrozenJuice[, "price"]/FrozenJuice[, "ppi"]
FOJC_pctc <- 100 * diff(log(FOJCPI))
FDD <- FrozenJuice[, "fdd"]

# convertir series a objetos xts
FOJCPI_xts <- as.xts(FOJCPI)
FDD_xts <- as.xts(FrozenJuice[, 3])

# graficar el índice de precios del jugo de naranja
plot(as.zoo(FOJCPI),
     col = "steelblue", 
     lwd = 2,
     xlab = "Fecha",
     ylab = "Índice de precio", 
     main = "Jugo de naranja concentrado congelado")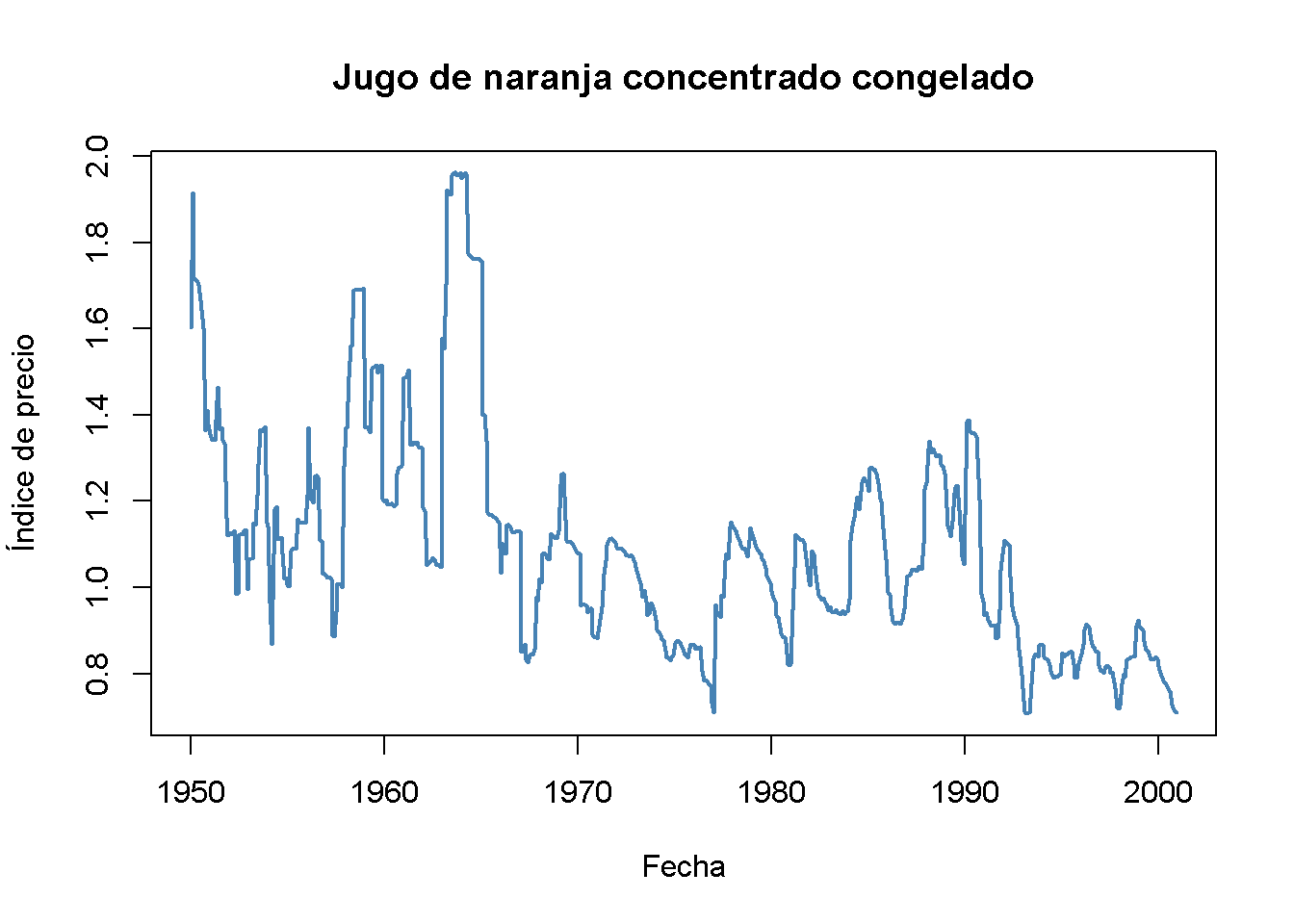

# dividir el área de graficado
par(mfrow = c(2, 1))

# graficar los cambios porcentuales en los precios
plot(as.zoo(FOJC_pctc),
     col = "steelblue", 
     lwd = 2,
     xlab = "Fecha",
     ylab = "Porcentaje",
     main = "Cambios mensuales en el precio del jugo de naranja concentrado congelado")

# graficar grados días de congelación
plot(as.zoo(FDD),
     col = "steelblue", 
     lwd = 2,
     xlab = "Fecha",
     ylab = "Grados días de congelación",
     main = "Días de grado de congelación mensuales en Orlando, FL")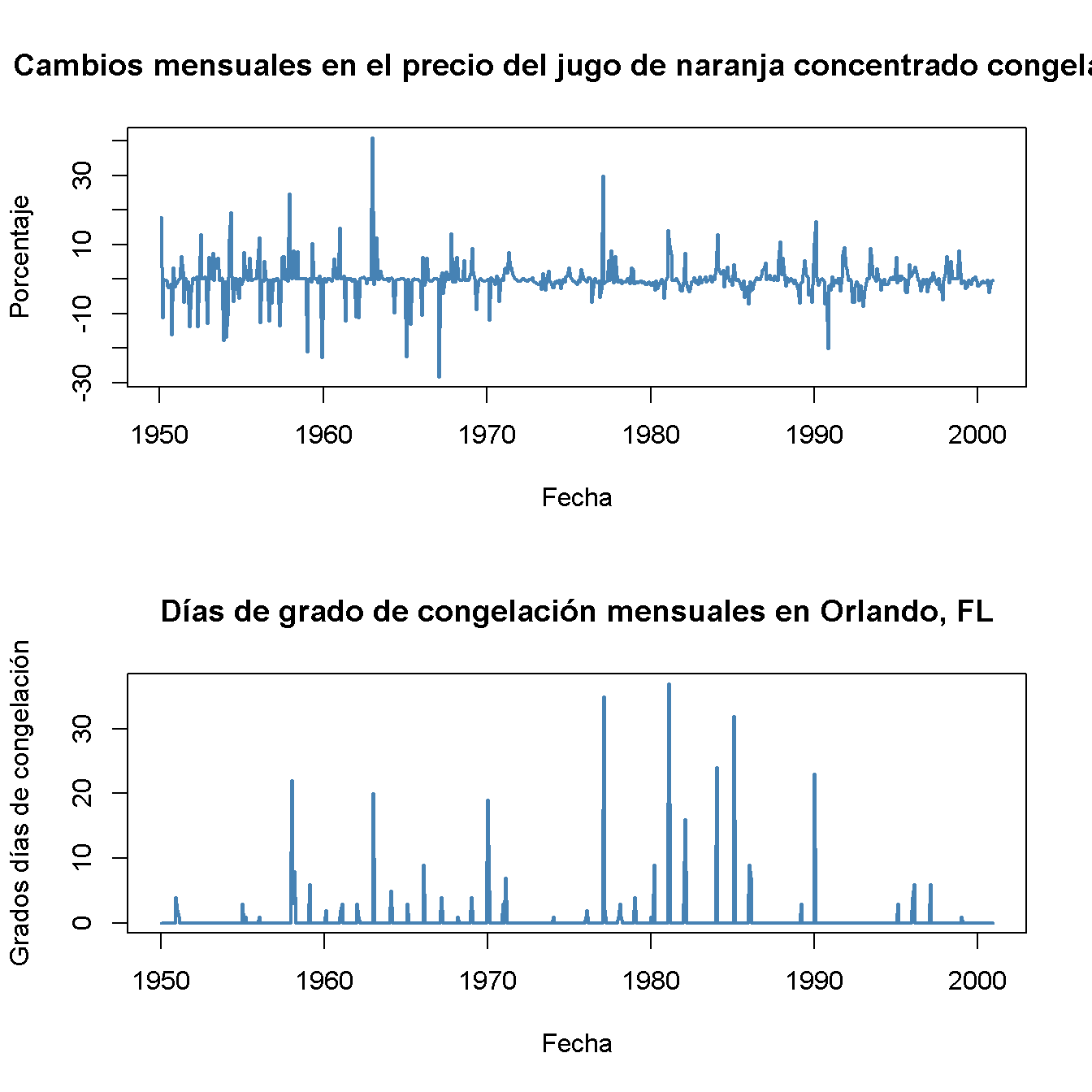

Los períodos con una gran cantidad de grados día de congelación son seguidos por grandes cambios de precios de mes a mes. Estos movimientos coincidentes motivan una regresión simple de los cambios de precio (\(\%ChgOJC_t\)) en grados día de congelación (\(FDD_t\)) para estimar el efecto de un día de grado de congelación adicional en el precio en el mes actual. Para ello, como para todas las demás regresiones de este capítulo, se usa \(T = 611\) observaciones (de enero de 1950 a diciembre de 2000).

# regresión simple de cambios porcentuales en grados día de congelación
orange_SR <- dynlm(FOJC_pctc ~ FDD)
coeftest(orange_SR, vcov. = vcovHAC)
#> 
#> t test of coefficients:
#> 
#>             Estimate Std. Error t value  Pr(>|t|)    
#> (Intercept) -0.42095    0.18683 -2.2531 0.0246064 *  
#> FDD          0.46724    0.13385  3.4906 0.0005167 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Observe que los errores estándar se calculan utilizando un estimador “HAC” de la matriz de varianza-covarianza; consulte el Capítulo 15.5 para una discusión de este estimador.

\[\begin{align*} \widehat{\%ChgOJC_t} = -\underset{(0.19)}{0.42} + \underset{(0.13)}{0.47} FDD_t \end{align*}\]

El coeficiente estimado en \(FDD_t\) tiene la siguiente interpretación: Un día de grado de congelación adicional en el mes \(t\) conduce a un aumento de precio de \(0.47\) puntos porcentuales en el mismo mes.

Para considerar los efectos de las olas de frío en el precio del jugo de naranja durante los períodos subsiguientes, se incluyen valores rezagados de \(FDD_t\) en el modelo, lo que conduce a un modelo de regresión de rezagos distribuidos. Se estima una especificación utilizando un valor contemporáneo y seis valores rezagados de \(FDD_t\) como regresores.

# modelo de retraso distribuido con 6 retrasos de grados día de congelación
orange_DLM <- dynlm(FOJC_pctc ~ FDD + L(FDD, 1:6))
coeftest(orange_DLM, vcov. = vcovHAC)
#> 
#> t test of coefficients:
#> 
#>               Estimate Std. Error t value  Pr(>|t|)    
#> (Intercept)  -0.692961   0.212445 -3.2618 0.0011700 ** 
#> FDD           0.471433   0.135195  3.4871 0.0005242 ***
#> L(FDD, 1:6)1  0.145021   0.081557  1.7782 0.0758853 .  
#> L(FDD, 1:6)2  0.058364   0.058911  0.9907 0.3222318    
#> L(FDD, 1:6)3  0.074166   0.047143  1.5732 0.1162007    
#> L(FDD, 1:6)4  0.036304   0.029335  1.2376 0.2163670    
#> L(FDD, 1:6)5  0.048756   0.031370  1.5543 0.1206535    
#> L(FDD, 1:6)6  0.050246   0.045129  1.1134 0.2659919    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Como resultado se obtiene:

\[\begin{align} \begin{split} \widehat{\%ChgOJC_t} =& -\underset{(0.21)}{0.69} + \underset{(0.14)}{0.47} FDD_t + \underset{(0.08)}{0.15} FDD_{t-1} + \underset{(0.06)}{0.06} FDD_{t-2} + \underset{(0.05)}{0.07} FDD_{t-3} \\ &+ \underset{(0.03)}{0.04} FDD_{t-4} + \underset{(0.03)}{0.05} FDD_{t-5} + \underset{(0.05)}{0.05} FDD_{t-6}, \end{split} \tag{16.1} \end{align}\]

donde el coeficiente de \(FDD_{t-1}\) estima el aumento de precio en el período \(t\) causado por un día de grado de congelación adicional en el mes anterior, el coeficiente de \(FDD_{t-2}\) estima el efecto de un día de grado de congelación hace dos meses y así sucesivamente. En consecuencia, los coeficientes en (16.1) pueden interpretarse como cambios de precio en períodos actuales y futuros debido a un aumento unitario en los grados día de congelación del mes actual.