8.6 Análisis del conjunto de datos de puntuación de la prueba
El capítulo 7 y algunas de las secciones anteriores han enfatizado que es importante incluir variables de control en los modelos de regresión si es plausible que haya factores omitidos. En el ejemplo de puntajes de pruebas, se quiere estimar el efecto causal de un cambio en la proporción alumno-maestro en los puntajes de las pruebas. Ahora se proporciona un ejemplo de cómo usar la regresión múltiple para aliviar el sesgo de las variables omitidas y demostrar cómo informar los resultados usando R.
Hasta ahora se han considerado dos variables que controlan las características no observables de los estudiantes, que se correlacionan con la proporción de estudiantes por maestro y se supone que tienen un impacto en los puntajes de las pruebas:
\(English\), el porcentaje de estudiantes que aprenden inglés
\(lunch\), la proporción de estudiantes que califican para un almuerzo subsidiado o incluso gratis en la escuela.
Otra nueva variable proporcionada con CASchools es calworks, el porcentaje de estudiantes que califican para el programa de asistencia de ingresos CalWorks. Los estudiantes elegibles para CalWorks viven en familias con un ingreso total por debajo del umbral del programa de almuerzo subsidiado, por lo que ambas variables son indicadores de la proporción de niños en desventaja económica. Ambos indicadores están altamente correlacionados:
# estimar la correlación entre 'calworks' y 'lunch'
cor(CASchools$calworks, CASchools$lunch)
#> [1] 0.7394218No existe una manera inequívoca de proceder al decidir qué variable usar. En cualquier caso, puede que no sea una buena idea utilizar ambas variables como regresores en vista de la colinealidad. Por lo tanto, también se consideran especificaciones de modelos alternativos.
Para empezar, se grafican las características de los estudiantes con los puntajes de las pruebas.
# configurar la disposición de las gráficas
m <- rbind(c(1, 2), c(3, 0))
graphics::layout(mat = m)
# gráfico de dispersión
plot(score ~ english,
data = CASchools,
col = "steelblue",
pch = 20,
xlim = c(0, 100),
cex.main = 0.9,
main = "Porcentaje de estudiantes de inglés")
plot(score ~ lunch,
data = CASchools,
col = "steelblue",
pch = 20,
cex.main = 0.9,
main = "Porcentaje que califica para el almuerzo a precio reducido")
plot(score ~ calworks,
data = CASchools,
col = "steelblue",
pch = 20,
xlim = c(0, 100),
cex.main = 0.9,
main = "Porcentaje que califica para asistencia económica")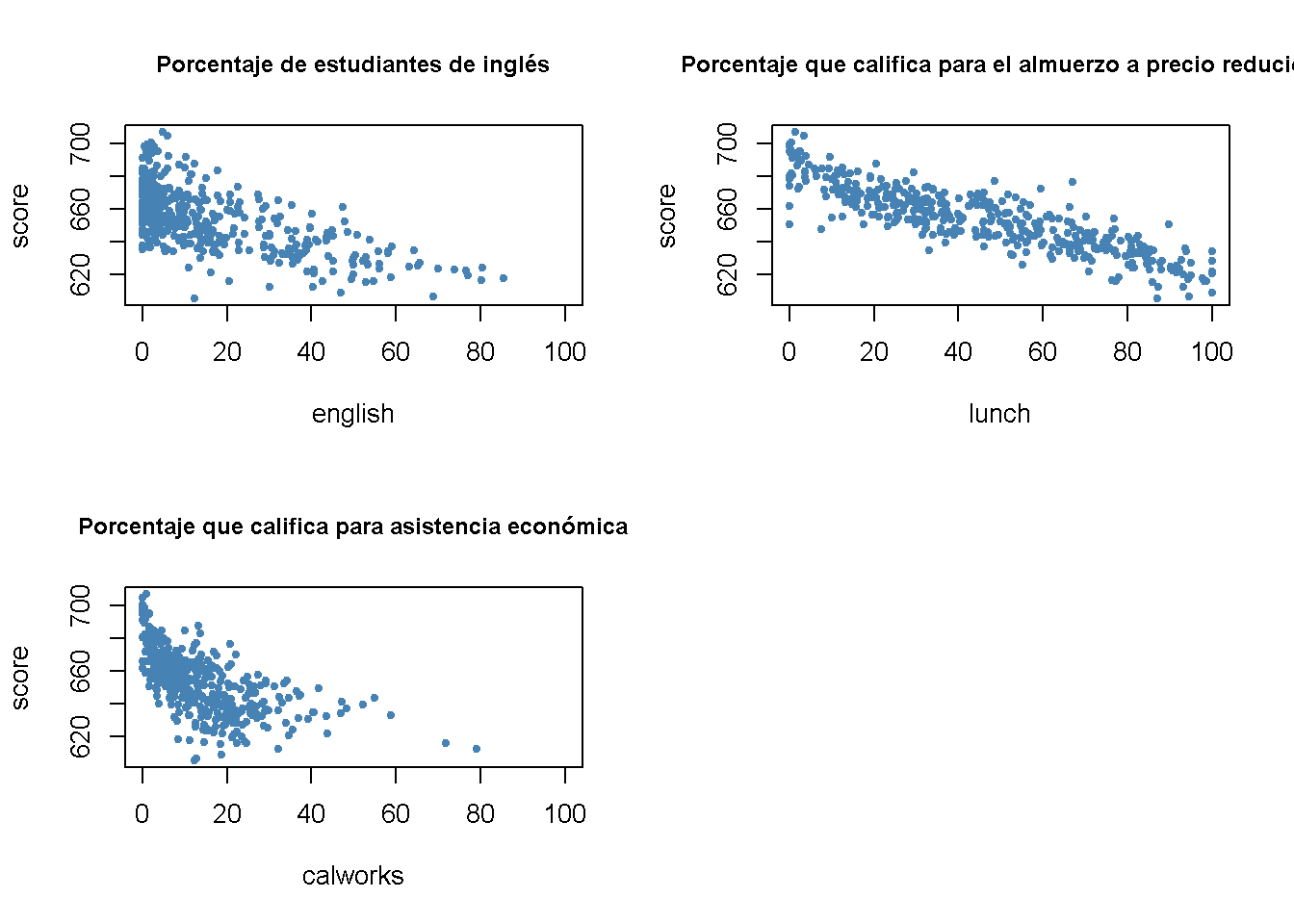
Se divide el área de graficado usando layout(). La matriz m especifica la ubicación de las gráficas, consultar ?layout.
Se puede ver que todas las relaciones son negativas. Aquí están los coeficientes de correlación:
# estimar la correlación entre las características de los estudiantes y los puntajes de las pruebas
cor(CASchools$score, CASchools$english)
#> [1] -0.6441238
cor(CASchools$score, CASchools$lunch)
#> [1] -0.868772
cor(CASchools$score, CASchools$calworks)
#> [1] -0.6268533Se consideran cinco ecuaciones modelo diferentes:
\[\begin{align*} (I) \quad TestScore=& \, \beta_0 + \beta_1 \times size + u, \\ (II) \quad TestScore=& \, \beta_0 + \beta_1 \times size + \beta_2 \times english + u, \\ (III) \quad TestScore=& \, \beta_0 + \beta_1 \times size + \beta_2 \times english + \beta_3 \times lunch + u, \\ (IV) \quad TestScore=& \, \beta_0 + \beta_1 \times size + \beta_2 \times english + \beta_4 \times calworks + u, \\ (V) \quad TestScore=& \, \beta_0 + \beta_1 \times size + \beta_2 \times english + \beta_3 \times lunch + \beta_4 \times calworks + u \end{align*}\]
La mejor forma de comunicar los resultados de la regresión es en una tabla. El paquete stargazer es muy conveniente para este propósito. Proporciona una función que genera tablas HTML y LaTeX de aspecto profesional que satisfacen los estándares científicos. Uno simplemente tiene que proporcionar uno o varios objetos de clase lm. El resto lo hace la función stargazer().
# cargar la biblioteca stargazer
library(stargazer)
# estimar diferentes especificaciones de modelo
spec1 <- lm(score ~ size, data = CASchools)
spec2 <- lm(score ~ size + english, data = CASchools)
spec3 <- lm(score ~ size + english + lunch, data = CASchools)
spec4 <- lm(score ~ size + english + calworks, data = CASchools)
spec5 <- lm(score ~ size + english + lunch + calworks, data = CASchools)
# recopilar errores estándar robustos en una lista
rob_se <- list(sqrt(diag(vcovHC(spec1, type = "HC1"))),
sqrt(diag(vcovHC(spec2, type = "HC1"))),
sqrt(diag(vcovHC(spec3, type = "HC1"))),
sqrt(diag(vcovHC(spec4, type = "HC1"))),
sqrt(diag(vcovHC(spec5, type = "HC1"))))
# generar una tabla LaTeX usando stargazer
stargazer(spec1, spec2, spec3, spec4, spec5,
se = rob_se,
digits = 3,
header = F,
column.labels = c("(I)", "(II)", "(III)", "(IV)", "(V)"))| Variable dependiente: Puntaje de la prueba | |||||
| score | |||||
| (I) | (II) | (III) | (IV) | (V) | |
| spec1 | spec2 | spec3 | spec4 | spec5 | |
| size | -2.280*** | -1.101** | -0.998*** | -1.308*** | -1.014*** |
| (0.519) | (0.433) | (0.270) | (0.339) | (0.269) | |
| english | -0.650*** | -0.122*** | -0.488*** | -0.130*** | |
| (0.031) | (0.033) | (0.030) | (0.036) | ||
| lunch | -0.547*** | -0.529*** | |||
| (0.024) | (0.038) | ||||
| calworks | -0.790*** | -0.048 | |||
| (0.068) | (0.059) | ||||
| Constant | 698.933*** | 686.032*** | 700.150*** | 697.999*** | 700.392*** |
| (10.364) | (8.728) | (5.568) | (6.920) | (5.537) | |
| Observations | 420 | 420 | 420 | 420 | 420 |
| R2 | 0.051 | 0.426 | 0.775 | 0.629 | 0.775 |
| Adjusted R2 | 0.049 | 0.424 | 0.773 | 0.626 | 0.773 |
| Residual Std. Error | 18.581 (df = 418) | 14.464 (df = 417) | 9.080 (df = 416) | 11.654 (df = 416) | 9.084 (df = 415) |
| F Statistic | 22.575*** (df = 1; 418) | 155.014*** (df = 2; 417) | 476.306*** (df = 3; 416) | 234.638*** (df = 3; 416) | 357.054*** (df = 4; 415) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | ||||
Table 8.1: Regresiones de los puntajes de las pruebas en la relación alumno-maestro y las variables de control
La tabla 8.1 establece que \(score\) es la variable dependiente y que se consideran cinco modelos. Se puede ver que las columnas de la Tabla 8.1 contienen la mayor parte de la información proporcionada por coeftest() y summary() para los modelos de regresión en consideración: Los coeficientes estimados equipados con códigos de significancia (los asteriscos) y errores estándar entre paréntesis. Aunque no existen estadísticos de \(t\), es sencillo para el lector calcularlas simplemente dividiendo una estimación de coeficiente por el error estándar correspondiente. La parte inferior de la tabla informa de estadísticas resumidas para cada modelo y una leyenda.
¿Qué se puede concluir de la comparación del modelo?
Se puede ver que la adición de variables de control reduce aproximadamente a la mitad el coeficiente de size. Además, la estimación no es sensible al conjunto de variables de control utilizadas. La conclusión es que la disminución de la proporción alumno-maestro ceteris paribus en una unidad conduce a un aumento promedio estimado en los puntajes de las pruebas de alrededor de \(1\) punto.
Agregar características de los estudiantes como controles aumenta \(R^2\) y \(\bar{R}^2\) desde \(0.049\) (spec1) hasta \(0.773\) (spec3 y spec5) , por lo que se pueden considerar estas variables como predictores adecuados para los resultados de las pruebas. Además, los coeficientes estimados en todas las variables de control son consistentes.
Se puede ver que las variables de control no son estadísticamente significativas en todos los modelos. Por ejemplo, en spec5, el coeficiente de \(calworks\) no es significativamente diferente de cero a \(5\%\) ya que \(\lvert-0.048/0.059\rvert=0.81 < 1.64\). También se puede observar que el efecto sobre la estimación (y su error estándar) del coeficiente sobre \(size\) de agregar \(calworks\) a la especificación base spec3 es insignificante. Por lo tanto, se puede considerar calworks como una variable de control superflua, dada la inclusión de lunch en este modelo.