11.1 Datos de panel
Concepto clave 10.1
Notación para datos de panel
En contraste con los datos de sección transversal donde se tienen observaciones sobre \(n\) sujetos (entidades), los datos de panel tienen observaciones sobre \(n\) entidades en períodos de tiempo \(T\geq2\). Esto se denota:
\[(X_{it},Y_{it}), \ i=1,\dots,n \ \ \ \text{and} \ \ \ t=1,\dots,T \]
donde el índice \(i\) se refiere a la entidad mientras que \(t\) se refiere al período de tiempo.
A veces, los datos de panel también se denominan datos longitudinales, ya que agregan una dimensión temporal a los datos transversales. Echando un vistazo al conjunto de datos Fatalities comprobando su estructura y enumerando las primeras observaciones.
# cargar el paquete y el conjunto de datos
library(AER)
data(Fatalities)# obtener la dimensión e inspeccionar la estructura
is.data.frame(Fatalities)
#> [1] TRUE
dim(Fatalities)
#> [1] 336 34str(Fatalities)
#> 'data.frame': 336 obs. of 34 variables:
#> $ state : Factor w/ 48 levels "al","az","ar",..: 1 1 1 1 1 1 1 2 2 2 ...
#> $ year : Factor w/ 7 levels "1982","1983",..: 1 2 3 4 5 6 7 1 2 3 ...
#> $ spirits : num 1.37 1.36 1.32 1.28 1.23 ...
#> $ unemp : num 14.4 13.7 11.1 8.9 9.8 ...
#> $ income : num 10544 10733 11109 11333 11662 ...
#> $ emppop : num 50.7 52.1 54.2 55.3 56.5 ...
#> $ beertax : num 1.54 1.79 1.71 1.65 1.61 ...
#> $ baptist : num 30.4 30.3 30.3 30.3 30.3 ...
#> $ mormon : num 0.328 0.343 0.359 0.376 0.393 ...
#> $ drinkage : num 19 19 19 19.7 21 ...
#> $ dry : num 25 23 24 23.6 23.5 ...
#> $ youngdrivers: num 0.212 0.211 0.211 0.211 0.213 ...
#> $ miles : num 7234 7836 8263 8727 8953 ...
#> $ breath : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...
#> $ jail : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 2 2 2 ...
#> $ service : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 2 2 2 ...
#> $ fatal : int 839 930 932 882 1081 1110 1023 724 675 869 ...
#> $ nfatal : int 146 154 165 146 172 181 139 131 112 149 ...
#> $ sfatal : int 99 98 94 98 119 114 89 76 60 81 ...
#> $ fatal1517 : int 53 71 49 66 82 94 66 40 40 51 ...
#> $ nfatal1517 : int 9 8 7 9 10 11 8 7 7 8 ...
#> $ fatal1820 : int 99 108 103 100 120 127 105 81 83 118 ...
#> $ nfatal1820 : int 34 26 25 23 23 31 24 16 19 34 ...
#> $ fatal2124 : int 120 124 118 114 119 138 123 96 80 123 ...
#> $ nfatal2124 : int 32 35 34 45 29 30 25 36 17 33 ...
#> $ afatal : num 309 342 305 277 361 ...
#> $ pop : num 3942002 3960008 3988992 4021008 4049994 ...
#> $ pop1517 : num 209000 202000 197000 195000 204000 ...
#> $ pop1820 : num 221553 219125 216724 214349 212000 ...
#> $ pop2124 : num 290000 290000 288000 284000 263000 ...
#> $ milestot : num 28516 31032 32961 35091 36259 ...
#> $ unempus : num 9.7 9.6 7.5 7.2 7 ...
#> $ emppopus : num 57.8 57.9 59.5 60.1 60.7 ...
#> $ gsp : num -0.0221 0.0466 0.0628 0.0275 0.0321 ...# enumerar las primeras observaciones
head(Fatalities)
#> state year spirits unemp income emppop beertax baptist mormon drinkage
#> 1 al 1982 1.37 14.4 10544.15 50.69204 1.539379 30.3557 0.32829 19.00
#> 2 al 1983 1.36 13.7 10732.80 52.14703 1.788991 30.3336 0.34341 19.00
#> 3 al 1984 1.32 11.1 11108.79 54.16809 1.714286 30.3115 0.35924 19.00
#> 4 al 1985 1.28 8.9 11332.63 55.27114 1.652542 30.2895 0.37579 19.67
#> 5 al 1986 1.23 9.8 11661.51 56.51450 1.609907 30.2674 0.39311 21.00
#> 6 al 1987 1.18 7.8 11944.00 57.50988 1.560000 30.2453 0.41123 21.00
#> dry youngdrivers miles breath jail service fatal nfatal sfatal
#> 1 25.0063 0.211572 7233.887 no no no 839 146 99
#> 2 22.9942 0.210768 7836.348 no no no 930 154 98
#> 3 24.0426 0.211484 8262.990 no no no 932 165 94
#> 4 23.6339 0.211140 8726.917 no no no 882 146 98
#> 5 23.4647 0.213400 8952.854 no no no 1081 172 119
#> 6 23.7924 0.215527 9166.302 no no no 1110 181 114
#> fatal1517 nfatal1517 fatal1820 nfatal1820 fatal2124 nfatal2124 afatal
#> 1 53 9 99 34 120 32 309.438
#> 2 71 8 108 26 124 35 341.834
#> 3 49 7 103 25 118 34 304.872
#> 4 66 9 100 23 114 45 276.742
#> 5 82 10 120 23 119 29 360.716
#> 6 94 11 127 31 138 30 368.421
#> pop pop1517 pop1820 pop2124 milestot unempus emppopus gsp
#> 1 3942002 208999.6 221553.4 290000.1 28516 9.7 57.8 -0.02212476
#> 2 3960008 202000.1 219125.5 290000.2 31032 9.6 57.9 0.04655825
#> 3 3988992 197000.0 216724.1 288000.2 32961 7.5 59.5 0.06279784
#> 4 4021008 194999.7 214349.0 284000.3 35091 7.2 60.1 0.02748997
#> 5 4049994 203999.9 212000.0 263000.3 36259 7.0 60.7 0.03214295
#> 6 4082999 204999.8 208998.5 258999.8 37426 6.2 61.5 0.04897637# resumir las variables 'state' y 'year'
summary(Fatalities[, c(1, 2)])
#> state year
#> al : 7 1982:48
#> az : 7 1983:48
#> ar : 7 1984:48
#> ca : 7 1985:48
#> co : 7 1986:48
#> ct : 7 1987:48
#> (Other):294 1988:48Se encuentra que el conjunto de datos consta de 336 observaciones sobre 34 variables. Se puede observar que la variable state es una variable de factor con 48 niveles (uno para cada uno de los 48 estados federales contiguos de los EE. UU.).
La variable year también es una variable factorial que tiene 7 niveles que identifican el período de tiempo en que se realizó la observación. Esto nos da \(7\times48 = 336\) observaciones en total. Dado que todas las variables se observan para todas las entidades y durante todos los períodos de tiempo, el panel está equilibrado. Si faltaran datos para al menos una entidad en al menos un período de tiempo, se llamarían datos de panel desequilibrado.
Ejemplo: Muertes por accidentes de tránsito e impuestos sobre el alcohol
Se debe comenzar con la creación de un gráfico. Para ello, se estiman regresiones simples utilizando datos de los años 1982 y 1988 que modelan la relación entre el impuesto a la cerveza (ajustado por dólares de 1988) y la tasa de fatalidades de tránsito, medida como el número de fatalidades por 10000 habitantes. Luego, se grafican los datos y se agregan las funciones de regresión estimadas correspondientes.
# definir la tasa de letalidad
Fatalities$fatal_rate <- Fatalities$fatal / Fatalities$pop * 10000
# subconjunto de los datos
Fatalities1982 <- subset(Fatalities, year == "1982")
Fatalities1988 <- subset(Fatalities, year == "1988")# estimar modelos de regresión simple usando datos de 1982 y 1988
fatal1982_mod <- lm(fatal_rate ~ beertax, data = Fatalities1982)
fatal1988_mod <- lm(fatal_rate ~ beertax, data = Fatalities1988)
coeftest(fatal1982_mod, vcov. = vcovHC, type = "HC1")
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.01038 0.14957 13.4408 <2e-16 ***
#> beertax 0.14846 0.13261 1.1196 0.2687
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
coeftest(fatal1988_mod, vcov. = vcovHC, type = "HC1")
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.85907 0.11461 16.2205 < 2.2e-16 ***
#> beertax 0.43875 0.12786 3.4314 0.001279 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Las funciones de regresión estimadas son:
\[\begin{align*} \widehat{\text{Tasa de fatalidad}} =& \, \underset{(0.15)}{2.01} + \underset{(0.13)}{0.15} \times \text{Impuesto a la cerveza} \quad (\text{Datos de } 1982), \\ \widehat{\text{Tasa de fatalidad}} =& \, \underset{(0.11)}{1.86} + \underset{(0.13)}{0.44} \times \text{Impuesto a la cerveza} \quad (\text{Datos de } 1988). \end{align*}\]
# graficar las observaciones y agregar la línea de regresión estimada para los datos de 1982
plot(x = Fatalities1982$beertax,
y = Fatalities1982$fatal_rate,
xlab = "Impuesto a la cerveza (en dólares de 1988)",
ylab = "Tasa de mortalidad (muertes por 10000)",
main = "Tasas de accidentes de tráfico e impuestos a la cerveza en 1982",
ylim = c(0, 4.5),
pch = 20,
col = "steelblue")
abline(fatal1982_mod, lwd = 1.5)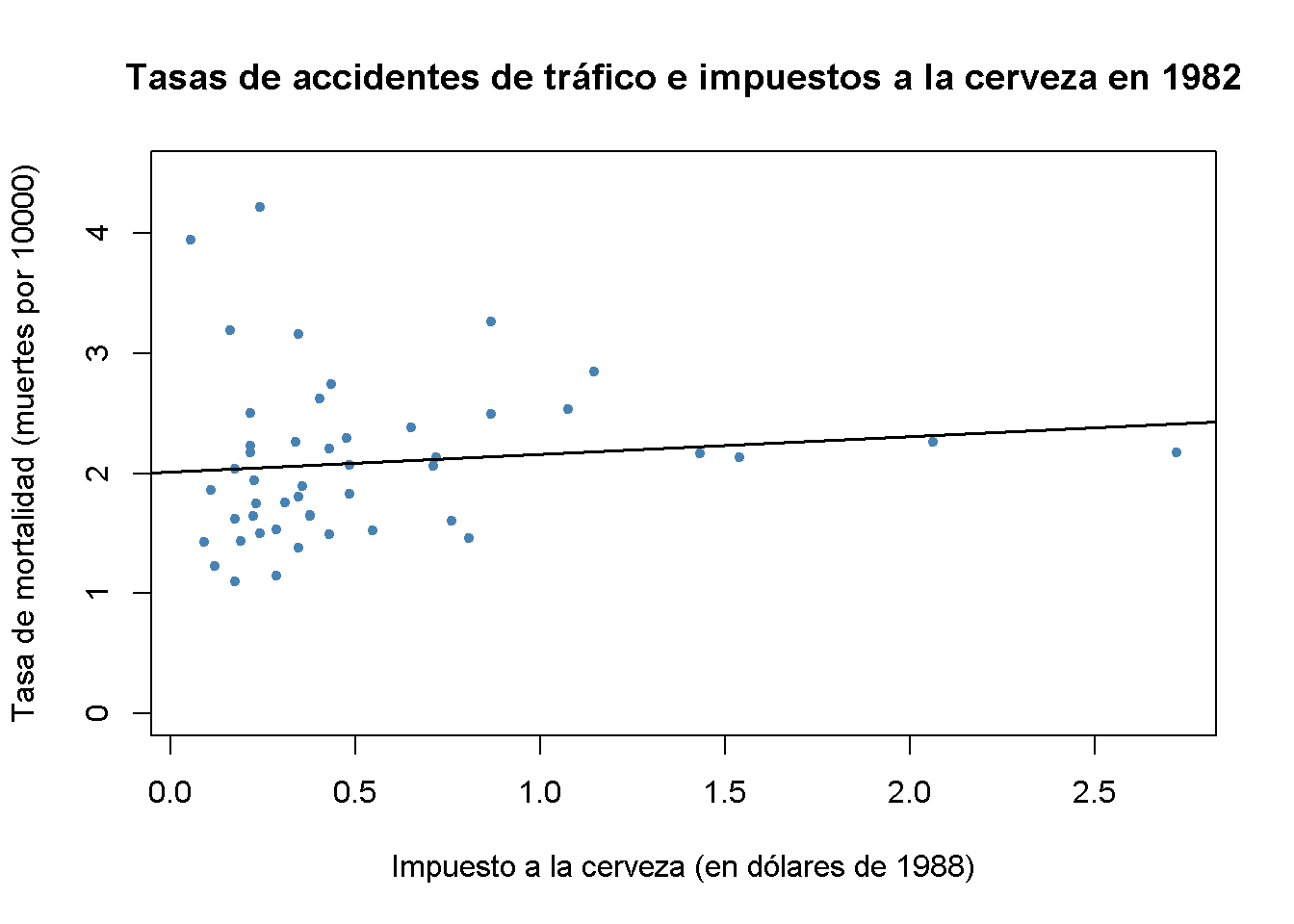
# graficar las observaciones y agregar la línea de regresión estimada para los datos de 1988
plot(x = Fatalities1988$beertax,
y = Fatalities1988$fatal_rate,
xlab = "Impuesto a la cerveza (en dólares de 1988)",
ylab = "Tasa de mortalidad (muertes por 10000)",
main = "Tasas de accidentes de tráfico e impuestos a la cerveza en 1988",
ylim = c(0, 4.5),
pch = 20,
col = "steelblue")
abline(fatal1988_mod, lwd = 1.5)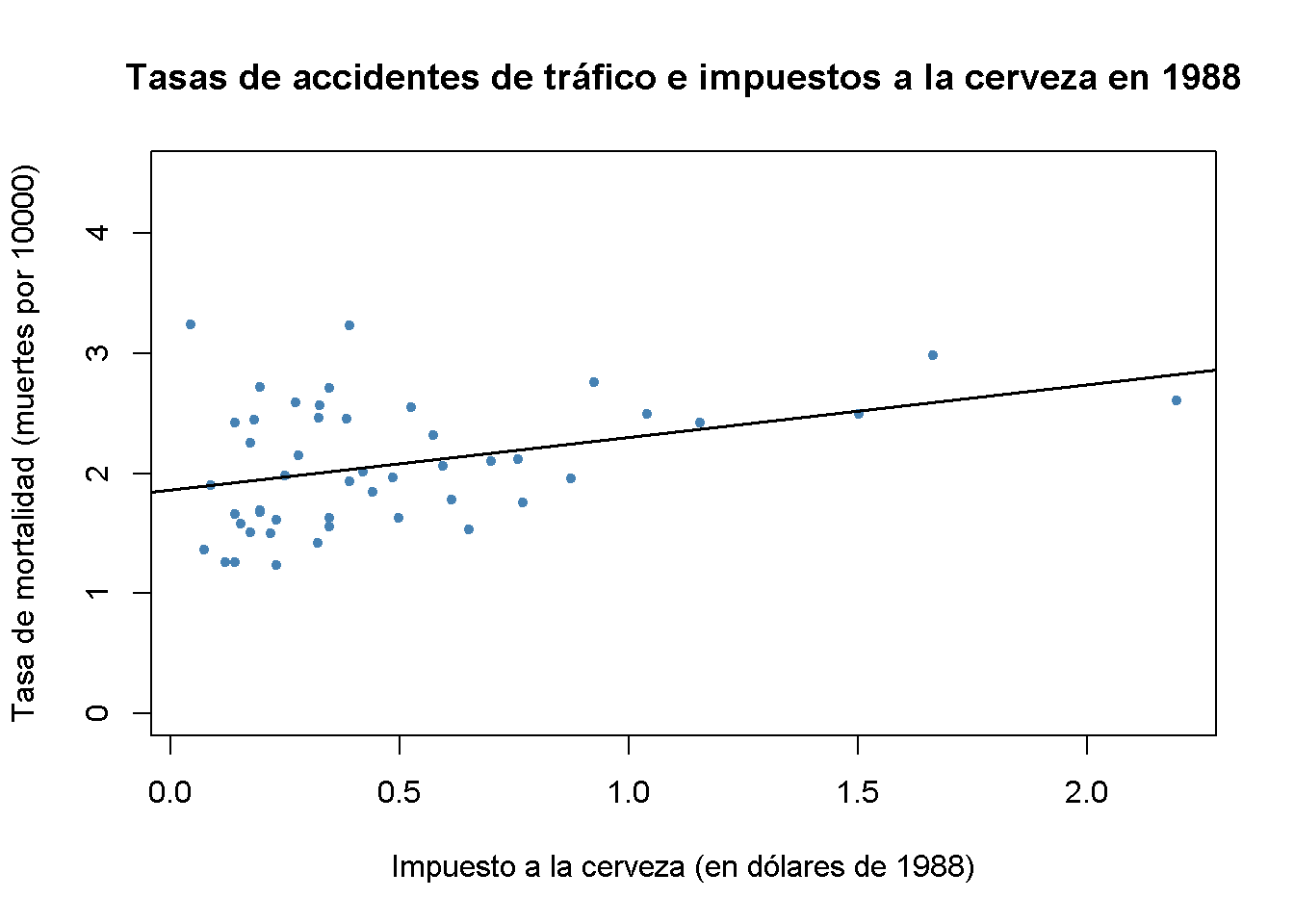
En ambas gráficas, cada punto representa las observaciones del impuesto a la cerveza y la tasa de mortalidad para un estado dado en el año respectivo. Los resultados de la regresión indican una relación positiva entre el impuesto a la cerveza y la tasa de letalidad para ambos años. El coeficiente estimado del impuesto a la cerveza para los datos de 1988 es casi tres veces mayor que el del conjunto de datos de 1988. Esto es contrario a las expectativas: Se supone que los impuestos sobre el alcohol reducen la tasa de accidentes de tránsito. Como se sabe por el Capítulo 7, esto posiblemente se deba al sesgo de la variable omitida, ya que ambos modelos no incluyen ninguna covariable; por ejemplo, condiciones económicas. Esto podría corregirse mediante el uso de un enfoque de regresión múltiple. Sin embargo, esto no puede tener en cuenta los factores omitidos no observables que difieren de un estado a otro, pero se puede suponer que son constantes durante el período de observación; por ejemplo, la actitud de la población hacia la conducción bajo los efectos del alcohol. Como se muestra en la siguiente sección, los datos de panel nos permiten mantener dichos factores constantes.