4.7 Diagramas de dispersión, covarianza de muestra y correlación de muestra
Un diagrama de dispersión representa datos bidimensionales, por ejemplo \(n\) observación en \(X_i\) y \(Y_i\), por puntos en un sistema de coordenadas. Es muy fácil generar gráficos de dispersión usando la función plot() en R. Es momento de generar algunos datos artificiales sobre la edad y los ingresos de los trabajadores y trazar un gráfico.
# establecer semilla aleatoria
set.seed(123)
# generar conjunto de datos
X <- runif(n = 100,
min = 18,
max = 70)
Y <- X + rnorm(n=100, 50, 15)
# graficar observaciones
plot(X,
Y,
type = "p",
main = "Una gráfica de dispersión de X e Y",
xlab = "Edad",
ylab = "Ganancias",
col = "steelblue",
pch = 19)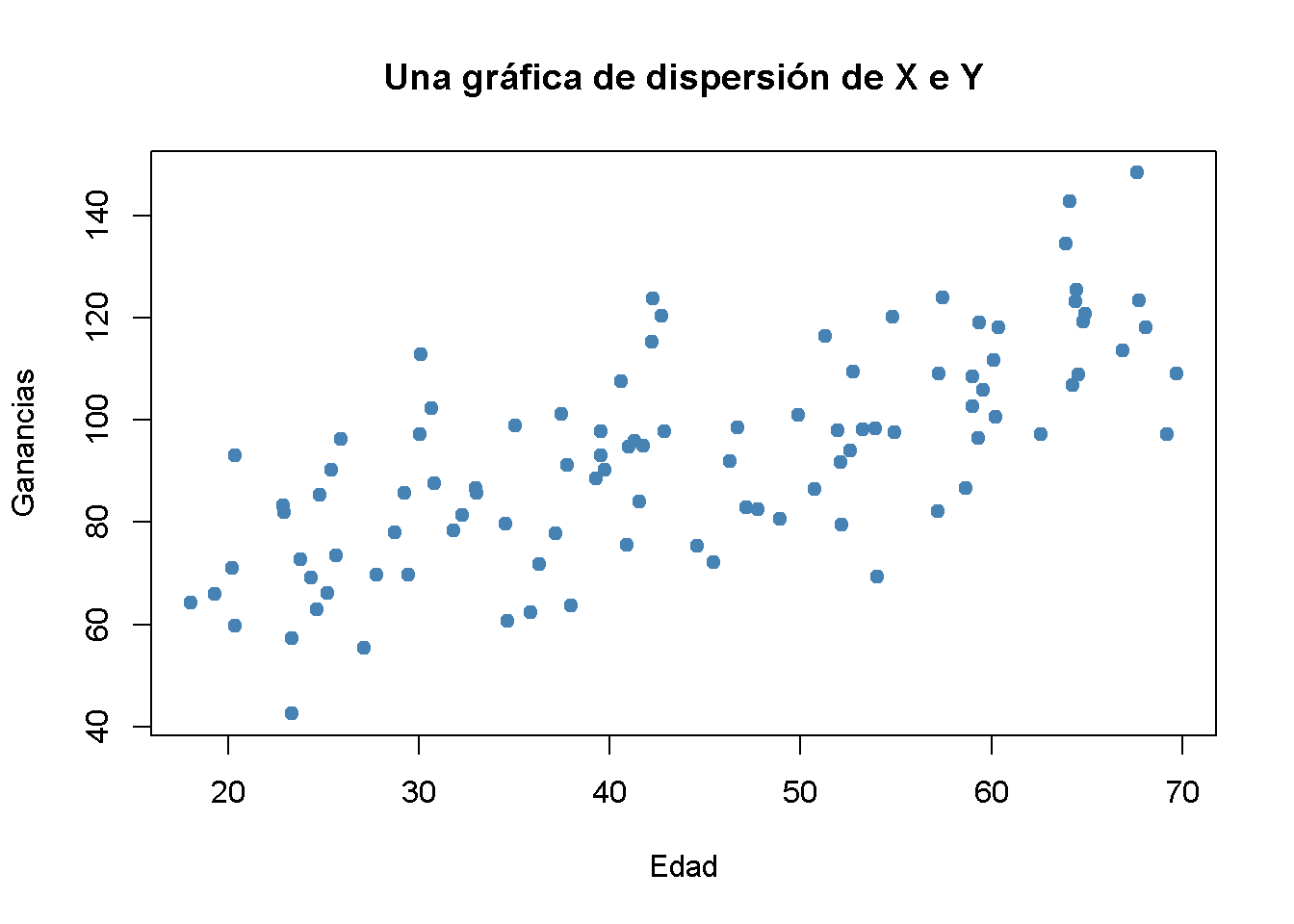
El gráfico muestra una correlación positiva entre la edad y los ingresos. Esto está en consonancia con la noción de que los trabajadores de más edad ganan más que los que se incorporaron recientemente a la población activa.
Covarianza y correlación de muestra
A estas alturas debería estar familiarizado con los conceptos de varianza y covarianza. Si no es así:
La varianza es una medida de dispersión definida como la esperanza del cuadrado de la desviación de una variable aleatoria respecto a su media. La varianza tiene como valor mínimo 0 y puede verse muy influida por los valores atípicos; por tanto, no se aconseja su uso cuando las distribuciones de las variables aleatorias tienen colas pesadas.
La covarianza es una medida de variabilidad entre dos variables. Implica que el aumento del valor de una variable se corresponde con el aumento del valor de otra, lo que da como resultado una covarianza positiva. Cuando el valor de una variable aumenta, mientras que el valor de otra disminuye, se dice que la covarianza es negativa. La covarianza muestra la relación lineal entre ambas variables, aunque la magnitud de la covarianza es difícil de interpretar. En este sentido, la correlación es la versión normalizada de la covarianza.
Al igual que la varianza, covarianza y correlación de dos variables son propiedades que se relacionan con la distribución de probabilidad conjunta (desconocida) de las variables. Se puede estimar la covarianza y la correlación mediante estimadores adecuados utilizando una muestra \((X_i, Y_i)\), \(i = 1, \dots, n\).
La covarianza de la muestra
\[ s_{XY} = \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline{X})(Y_i - \overline{Y}) \]
es un estimador de la varianza poblacional de \(X\) y \(Y\), mientras que la correlación muestral
\[ r_{XY} = \frac{s_{XY}}{s_Xs_Y} \]
se puede utilizar para estimar la correlación poblacional, una medida estandarizada de la fuerza de la relación lineal entre \(X\) y \(Y\).
En cuanto a la varianza y la desviación estándar, estos estimadores se implementan como funciones R en el paquete stats. Se pueden usar para estimar la covarianza poblacional y la correlación poblacional de los datos artificiales sobre edad e ingresos.
# calcular la covarianza de muestra de X e Y
cov(X, Y)
#> [1] 213.934
# calcular la correlación de la muestra entre X e Y
cor(X, Y)
#> [1] 0.706372
# una forma equivalente de calcular la correlación de la muestra
cov(X, Y) / (sd(X) * sd(Y))
#> [1] 0.706372Las estimaciones indican que \(X\) y \(Y\) tienen una correlación moderada.
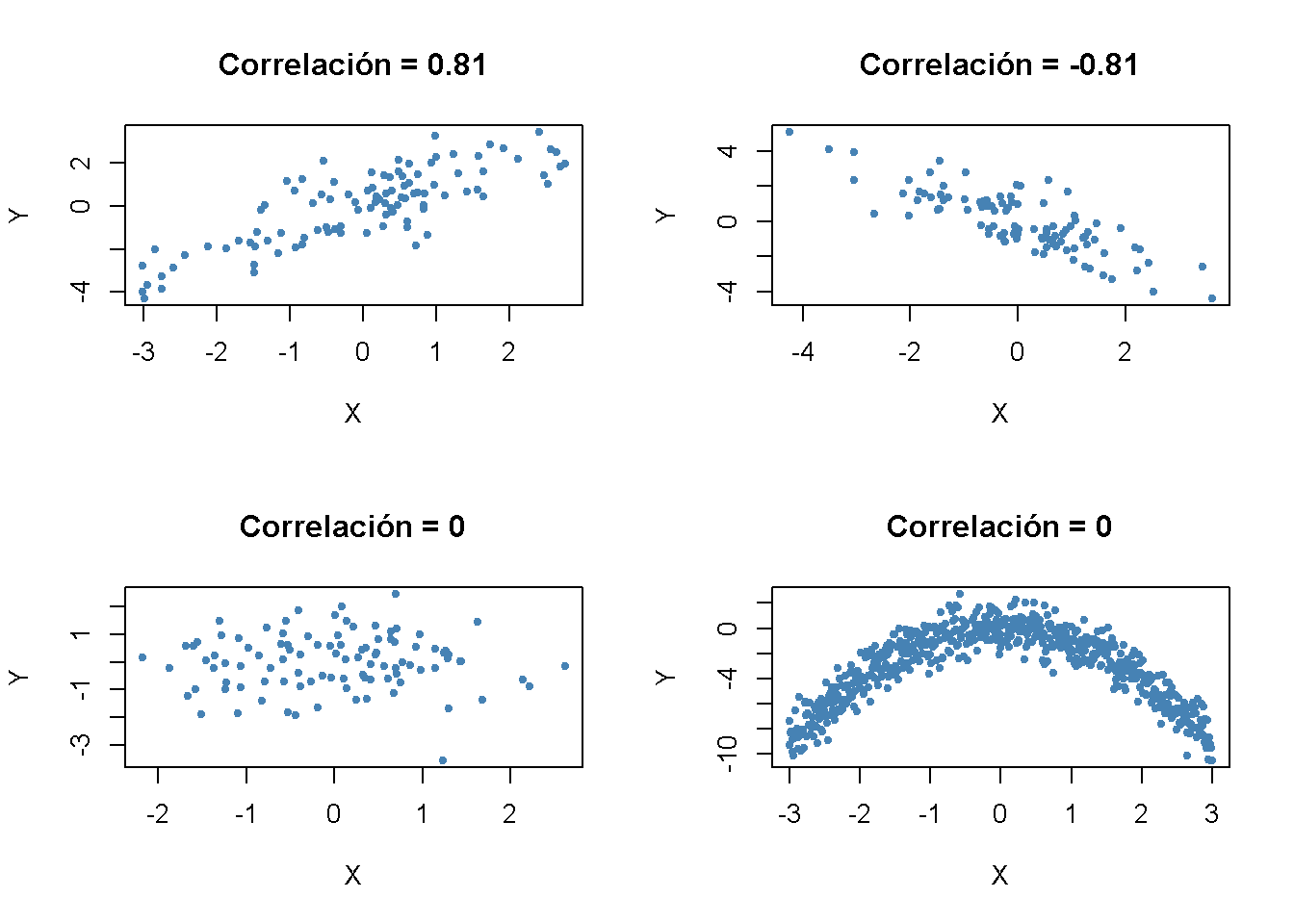
El siguiente fragmento de código usa la función mvnorm() del paquete MASS (Ripley 2021) para generar datos de muestra bivariados con diferentes grados de correlación.
library(MASS)
# establecer semilla aleatoria
set.seed(1)
# correlación positiva (0,81)
example1 <- mvrnorm(100,
mu = c(0, 0),
Sigma = matrix(c(2, 2, 2, 3), ncol = 2),
empirical = TRUE)
# correlación negativa (-0,81)
example2 <- mvrnorm(100,
mu = c(0, 0),
Sigma = matrix(c(2, -2, -2, 3), ncol = 2),
empirical = TRUE)
# sin correlación
example3 <- mvrnorm(100,
mu = c(0, 0),
Sigma = matrix(c(1, 0, 0, 1), ncol = 2),
empirical = TRUE)
# sin correlación (relación cuadrática)
X <- seq(-3, 3, 0.01)
Y <- - X^2 + rnorm(length(X))
example4 <- cbind(X, Y)
# dividir el área de la gráfica como una matriz de 2 por 2
par(mfrow = c(2, 2))
# plot datasets
plot(example1, col = "steelblue", pch = 20, xlab = "X", ylab = "Y",
main = "Correlación = 0.81")
plot(example2, col = "steelblue", pch = 20, xlab = "X", ylab = "Y",
main = "Correlación = -0.81")
plot(example3, col = "steelblue", pch = 20, xlab = "X", ylab = "Y",
main = "Correlación = 0")
plot(example4, col = "steelblue", pch = 20, xlab = "X", ylab = "Y",
main = "Correlación = 0")